详解Dijkstra算法原理及其C++实现

目录

• 什么是最短路径问题
• Dijkstra算法
• 实现思路
• 案例分析
• 代码实现

什么是最短路径问题

如果从图中某一顶点（称为源点）到达另一顶点（称为终点）的路径可能不止一条，如何找到一条路径使得沿此路径上各边上的权值总和达到最小。

单源最短路径问题是指对于给定的图G=(V,E)，求源点v₀到其它顶点v_t的最短路径。

Dijkstra算法

Dijkstra算法用于计算一个节点到其他节点的最短路径。Dijkstra是一种按路径长度递增的顺序逐步产生最短路径的方法，是一种贪婪算法。

Dijkstra算法的核心思想是首先求出长度最短的一条最短路径，再参照它求出长度次短的一条最短路径，依次类推，直到从源点v₀到其它各顶点的最短路径全部求出为止。

具体来说：图中所有顶点分成两组，第一组是已确定最短路径的顶点，初始只包含一个源点，记为集合S；第二组是尚未确定最短路径的顶点，记为集合U。

按最短路径长度递增的顺序逐个把U中的顶点加到S中去，同时动态更新U集合中源点到各个顶点的最短距离，直至所有顶点都包括到S中。

实现思路

1.初始时，S集合只包含起点v₀；U集合包含除v₀外的其他顶点v_t，且U中顶点的距离为起点v₀到该顶点的距离。（U 中顶点v_t的距离为(v₀,v_t)的长度，如果v₀和v_t不相邻，则v_t的最短距离为∞）

2.从U中选出距离最短的顶点v_t′，并将顶点v_t′加入到S中；同时，从U中移除顶点v_t′。

3.更新U中各个顶点v_t到起点v₀的距离以及最短路径中当前顶点的前驱顶点。之所以更新U中顶点的距离以及前驱顶点是由于上一步中确定了v_t′是求出最短路径的顶点，从而可以利用v_t′来更新U中其它顶点v_t的距离，因为存在(v₀,v_t)的距离可能大于(v₀,v_t')+(v_t',v_t)距离的情况，从而也需要更新其前驱顶点

4.重复步骤(2)和(3)，直到遍历完所有顶点

案例分析

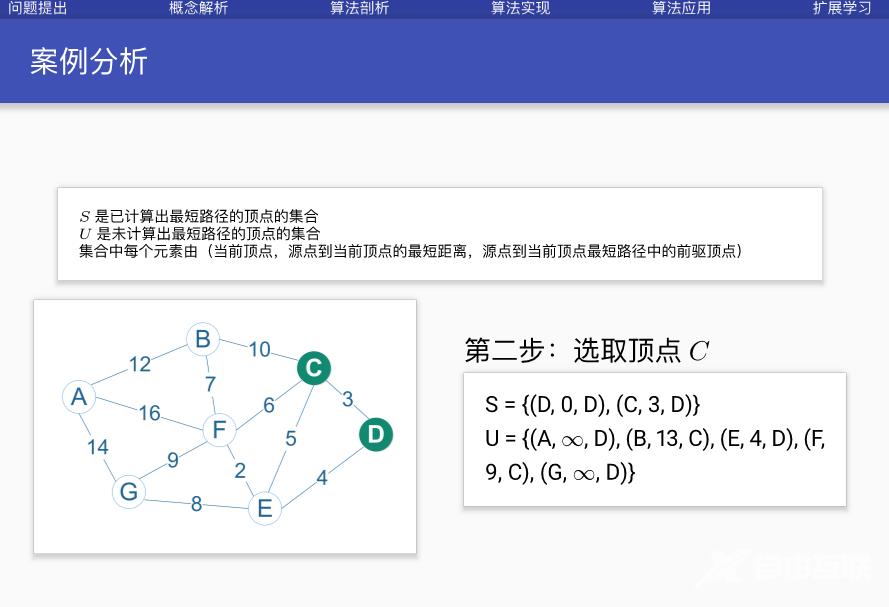
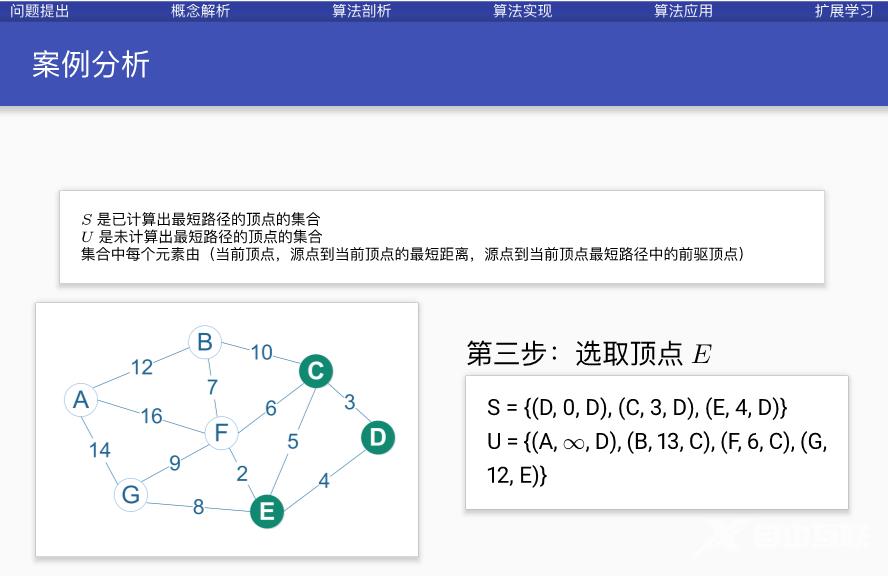
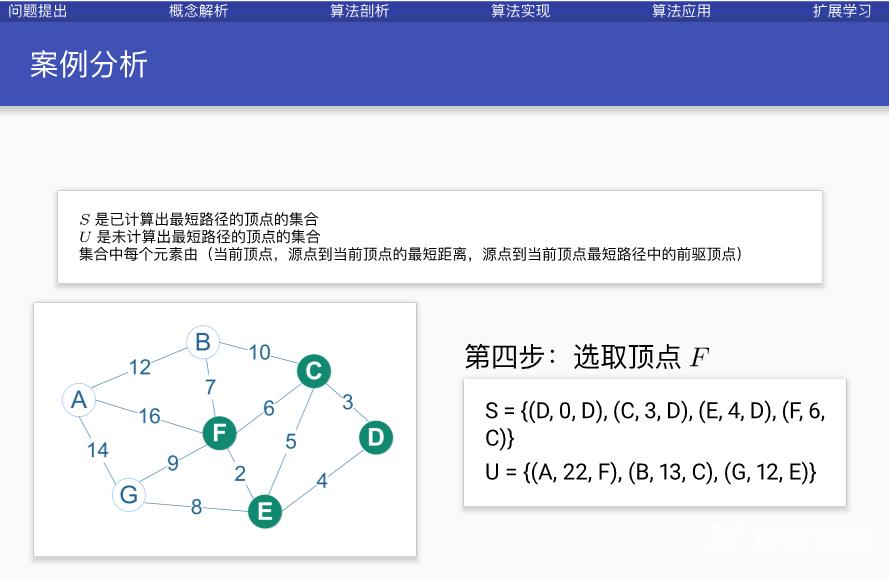
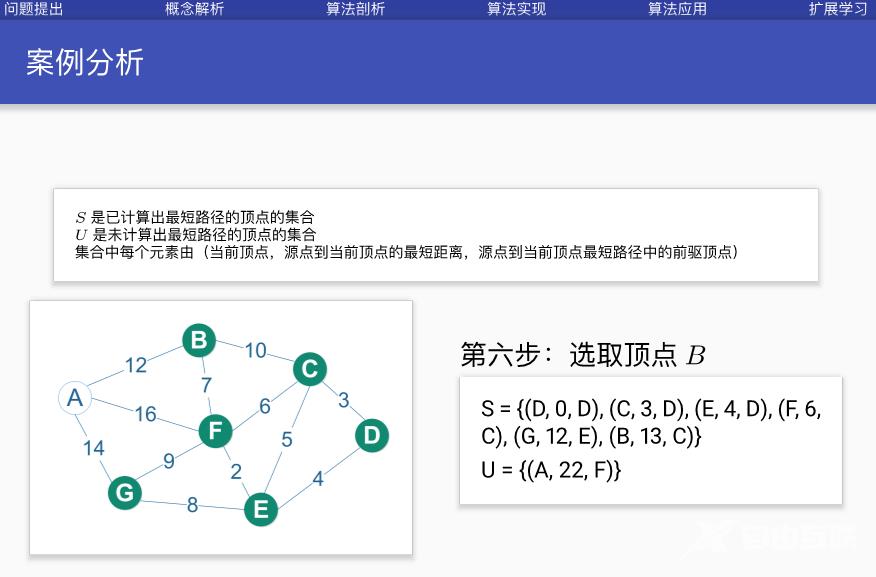
代码实现

使用了部分C++11特性，注释丰富，读起来应该不会太困难！

#include <cstdio>
#include <iostream>
#include <vector>
#include <list>
#include <stack>

using namespace std;
using Matrix = vector<vector<uint>>;                // 连接矩阵（使用嵌套的vector表示）
using SNodes = vector<tuple<uint, uint, uint>>;     // 已计算出最短路径的顶点集合S（类似一个动态数组）
using UNodes = list<tuple<uint, uint, uint>>;       // 未进行遍历的顶点集合U（使用list主要是方便元素删除操作）
using ENode = tuple<uint, uint, uint>;              // 每个节点包含（顶点编号，当前顶点到起始点最短距离，最短路径中当前顶点的上一个顶点）信息


/***
 * 从未遍历的U顶点集合中找到下一个离起始顶点距离最短的顶点
 * @param unvisitedNodes 未遍历的U顶点集合
 * 每个元素是（顶点编号，当前顶点到起始点最短距离，最短路径中当前顶点的上一个顶点）的tuple
 * @return 下一个离起始顶点距离最短的顶点
 */
ENode searchNearest(const UNodes &unvisitedNodes) {
    uint minDistance = UINT_MAX;
    ENode nearest;
    for (const auto &node: unvisitedNodes) {
        if (get<1>(node) <= minDistance) {
            minDistance = get<1>(node);
            nearest = node;
        }
    }
    return nearest;
}


/***
 * 迪克斯特拉算法的实现
 * @param graph 连接矩阵（使用嵌套的vector表示）
 * @param startNodeIndex 起始点编码（从0开始）
 * @return 返回一个vector，每个元素是到起始顶点的距离排列的包含（顶点编号，当前顶点到起始点最短距离，最短路径中当前顶点的上一个顶点）的tuple
 */
SNodes dijkstra(const Matrix &graph, uint startNodeIndex) {
    const uint numOfNodes = graph.size();   // 图中顶点的个数
    // S是已计算出最短路径的顶点的集合（顶点编号，当前顶点到起始点最短距离，最短路径中当前顶点的上一个顶点）
    SNodes visitedNodes;
    // U是未计算出最短路径的顶点的集合（其中的key为顶点编号，value为到起始顶点最短距离和最短路径中上一个节点编号组成的pair）
    UNodes unvisitedNodes;

    // 对S和U集合进行初始化，起始顶点的距离为0，其他顶点的距离为无穷大
    // 最短路径中当前顶点的上一个顶点初始化为起始顶点，后面会逐步进行修正
    for (auto i = 0; i < numOfNodes; ++i) {
        if (i == startNodeIndex) visitedNodes.emplace_back(i, 0, startNodeIndex);
        else unvisitedNodes.emplace_back(i, graph[startNodeIndex][i], startNodeIndex);
    }

    while (!unvisitedNodes.empty()) {
        // 从U中找到距离起始顶点距离最短的顶点，加入S，同时从U中删除
        auto nextNode = searchNearest(unvisitedNodes);
        unvisitedNodes.erase(find(unvisitedNodes.begin(), unvisitedNodes.end(), nextNode));
        visitedNodes.emplace_back(nextNode);
        // 更新U集合中各个顶点的最短距离以及最短路径中的上一个顶点
        for (auto &node: unvisitedNodes) {
            // 更新的判断依据就是起始顶点到当前顶点（nextNode）距离加上当前顶点到U集合中顶点的距离小于原来起始顶点到U集合中顶点的距离
            // 更新最短距离的时候同时需要更新最短路径中的上一个顶点为nextNode
            if (graph[get<0>(nextNode)][get<0>(node)] != UINT_MAX &&
                graph[get<0>(nextNode)][get<0>(node)] + get<1>(nextNode) < get<1>(node)) {
                get<1>(node) = graph[get<0>(nextNode)][get<0>(node)] + get<1>(nextNode);
                get<2>(node) = get<0>(nextNode);
            }
        }
    }

    return visitedNodes;
}


/***
 * 对使用迪克斯特拉算法求解的最短路径进行打印输出
 * @param paths vector表示的最短路径集合
 * 每个元素是到起始顶点的距离排列的包含（顶点编号，当前顶点到起始点最短距离，最短路径中当前顶点的上一个顶点）的tuple
 */
void print(const SNodes &paths) {
    stack<int> tracks;  //从尾部出发，使用stack将每个顶点的最短路径中的前一个顶点入栈，然后出栈的顺序就是最短路径顺序
    // 第一个元素是起始点，从第二个元素进行打印输出
    for (auto it = ++paths.begin(); it != paths.end(); ++it) {
        // 打印头部信息
        printf("%c -> %c:\t Length: %d\t Paths: %c",
               char(get<0>(paths[0]) + 65),
               char(get<0>(*it) + 65),
               get<1>(*it),
               char(get<0>(paths[0]) + 65));
        auto pointer = *it;
        // 如果当前指针pointer指向的节点有中途节点（判断的条件是最短路径中的前一个节点不是起始点）
        while (get<2>(pointer) != get<0>(paths[0])) {
            tracks.push(get<0>(pointer));
            // Lambda表达式，使用find_if函数把当前顶点的前一个顶点从paths中找出来继续进行循环直到前一个节点就是起始点
            auto condition = [pointer](tuple<uint, uint, uint> x) { return get<0>(x) == get<2>(pointer); };
            pointer = *find_if(paths.begin(), paths.end(), condition);
        }
        tracks.push(get<0>(pointer));

        // 以出栈的顺序进行打印输出
        while (!tracks.empty()) {
            printf(" -> %c", char(tracks.top() + 65));
            tracks.pop();
        }
        printf("\n");
    }
}

int main() {
    Matrix graph = {
            {0,        12,       UINT_MAX, UINT_MAX, UINT_MAX, 16, 14},
            {12,       0,        10,       UINT_MAX, UINT_MAX, 7, UINT_MAX},
            {UINT_MAX, 10,       0, 3,               5,        6, UINT_MAX},
            {UINT_MAX, UINT_MAX, 3, 0,               4, UINT_MAX, UINT_MAX},
            {UINT_MAX, UINT_MAX, 5, 4,               0,        2,  8},
            {16,       7,        6,        UINT_MAX, 2,        9,  9},
            {14,       UINT_MAX, UINT_MAX, UINT_MAX, 8,        9,  0}
    };  // 图对应的连接矩阵
    auto results = dijkstra(graph, uint('D' - 65));          // 选取顶点C（大写字母A的ASCII编码是65）
    print(results);     // 打印输出结果
    return 0;
}

运行结果：

D -> C:     Length: 3     Paths: D -> C
D -> E:     Length: 4     Paths: D -> E
D -> F:     Length: 6     Paths: D -> E -> F
D -> G:     Length: 12     Paths: D -> E -> G
D -> B:     Length: 13     Paths: D -> C -> B
D -> A:     Length: 22     Paths: D -> E -> F -> A

以上就是详解Dijkstra算法原理及其C++实现的详细内容，更多关于C++ Dijkstra算法的资料请关注自由互联其它相关文章！