目录 前言 一、直接选择排序 1.1 算法思想 1.2代码实现 1.3直接选择排序的特征总结 二、堆排序 2.1 什么是堆? 2.2 判断是否是堆 2.3向下调整算法 2.4自底向上的建堆方式 2.5 代码实现 2.
目录
- 前言
- 一、直接选择排序
- 1.1 算法思想
- 1.2 代码实现
- 1.3 直接选择排序的特征总结
- 二、堆排序
- 2.1 什么是堆?
- 2.2 判断是否是堆
- 2.3 向下调整算法
- 2.4 自底向上的建堆方式
- 2.5 代码实现
- 2.6 堆排序的特性总结
- 2.7 堆排序的特性总结
前言
本期为大家带来的是常见排序算法中的选择排序,主要有直接选择排序以及——堆排序(有点难理解),包您一看就会,快来试试吧~
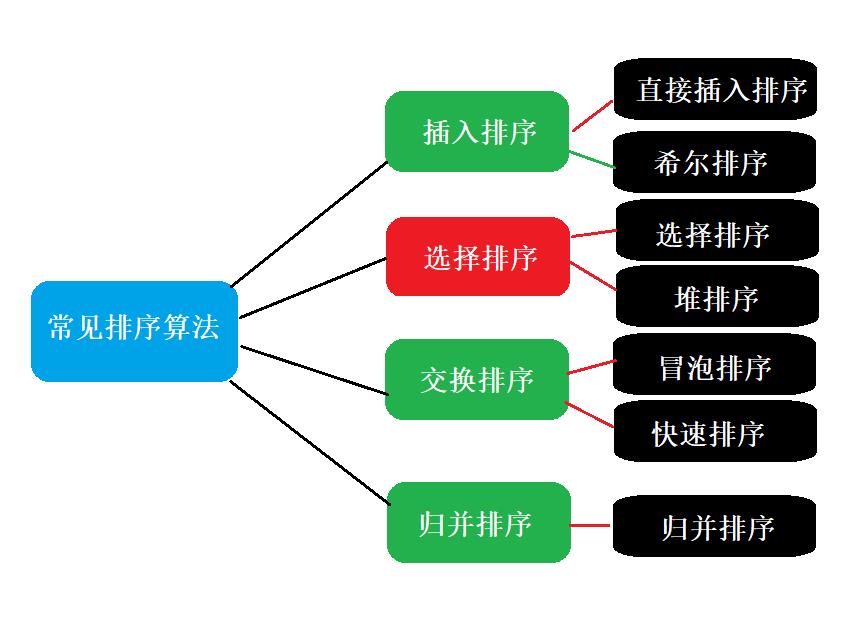
一、直接选择排序
1.1 算法思想
每一次从待排序的数据元素中选出最小(或最大的)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
在元素集合a[i]--a[n-1]中选择关键码最大(小)的数据元素 若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个) 元素交换 在剩余的 [a[i] , a[n-2] …… [a[i+1],a[n-1] ]集合中,重复上述步骤,直到集合剩 余1个元素。
我们拿一组实例来感受一下,直接选择排序是怎么运算的:

1.2 代码实现
给大家带来一个优化版本的直接选择排序,一次遍历,选出最大数和最小数,然后交换,相较于传统的,效率高了许多。
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
//交换
void Swap(int* mini, int* maxi)
{
int tmp = *mini;
*mini = *maxi;
*maxi = tmp;
}
//打印
void Print(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
}
//直接选择排序
void SelectSort(int *a,int n)
{
//下标
int begin = 0;
int end = n - 1;
while (begin < end)
{
int mini = begin, maxi = end;
//选出最大的给maxi,选出最小的给mini
for (int i=begin;i<=end;++i)
{
if (a[i]>a[mini])//升序
{
mini = i; //改两个if的符号即可实现升序、降序转换。
}
if (a[i] <a[maxi])
{
maxi = i;
}
}
//交换
Swap(&a[begin],&a[mini]);
//因为还有一种特殊情况,就是begin跟maxi重叠,然后执行第一次交换之后,maxi记录的是最小值
if (begin == maxi)
{
maxi = mini;
}
Swap(&a[end], &a[maxi]);
++begin;
--end;
}
}
直接选择排序
//void SelectSort(int* a, int n)//(升序)
//{
// for (int j=0;j<n-1;j++)//整体遍历
// {
// for (int i=j+1;i<n;i++)//遍历比较
// {
// if (a[j] > a[i])//比较交换
// {
// int tmp = a[j];
// a[j] = a[i];
// a[i] = tmp;
// }
// }
// }
//}
int main()
{
int a[10] = { 3,5,9,7,4,2,1,6,0,8 };
SelectSort(a, sizeof(a) / sizeof(a[0]));
//打印
Print(a, sizeof(a) / sizeof(a[0]));
return 0;
}
1.3 直接选择排序的特征总结
- 1.直接选择排序的算法非常好理解,但是效率不高,实际中也很少使用
- 2.时间复杂度:O(N^2) ,直接选择排序不管数据的顺序如何,都要遍历至结束
- 3.空间复杂度:O(1)
- 4.稳定性:不稳定
二、堆排序
2.1 什么是堆?
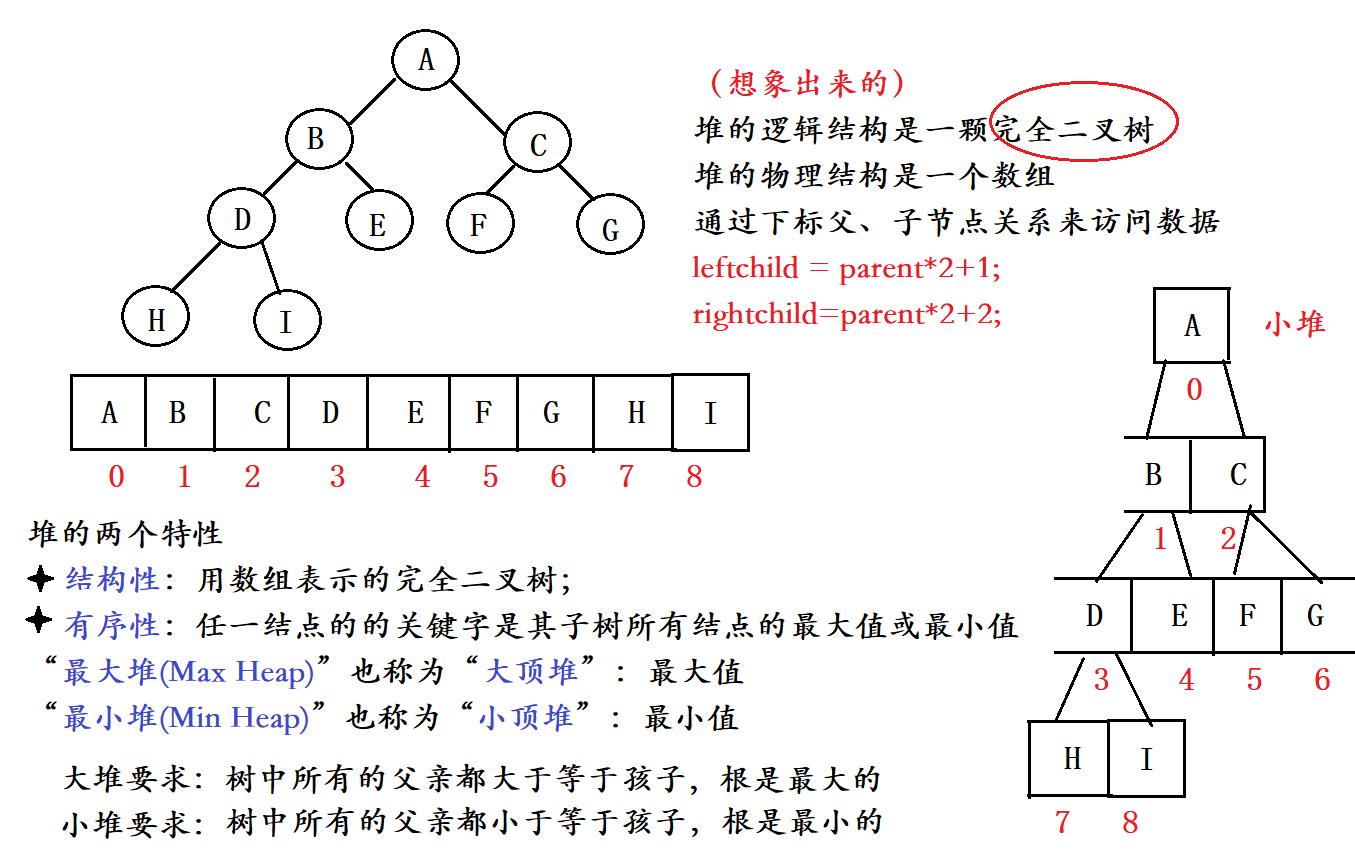
2.2 判断是否是堆

我们在给到一个数组的时候,里面的数据往往不是“堆”,我们在使用堆排序的时候,就需要建堆,
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种的排序算法,它是选择排序的一种,利用堆来进行选择数据。跟着我一起看看具体是怎么操作的。
建小堆排降序,建大堆排升序。
怎样建堆呢?这里我们的前辈就设计了一种算法
2.3 向下调整算法
堆排序的本质是选择排序
向下调整算法,如果是建小堆(排降序),前提:左右子树都是小堆。大堆就是反着来。
从根节点开始,选出左右孩子中小的那一个跟父亲比较,如果比父亲小就交换,然后继续往下调整,调整到叶子节点就停止。
2.4 自底向上的建堆方式
这种建堆方式是从倒数第二层的节点(叶子节点的上一层)开始,从右往左,从下到上的向下进行调整。
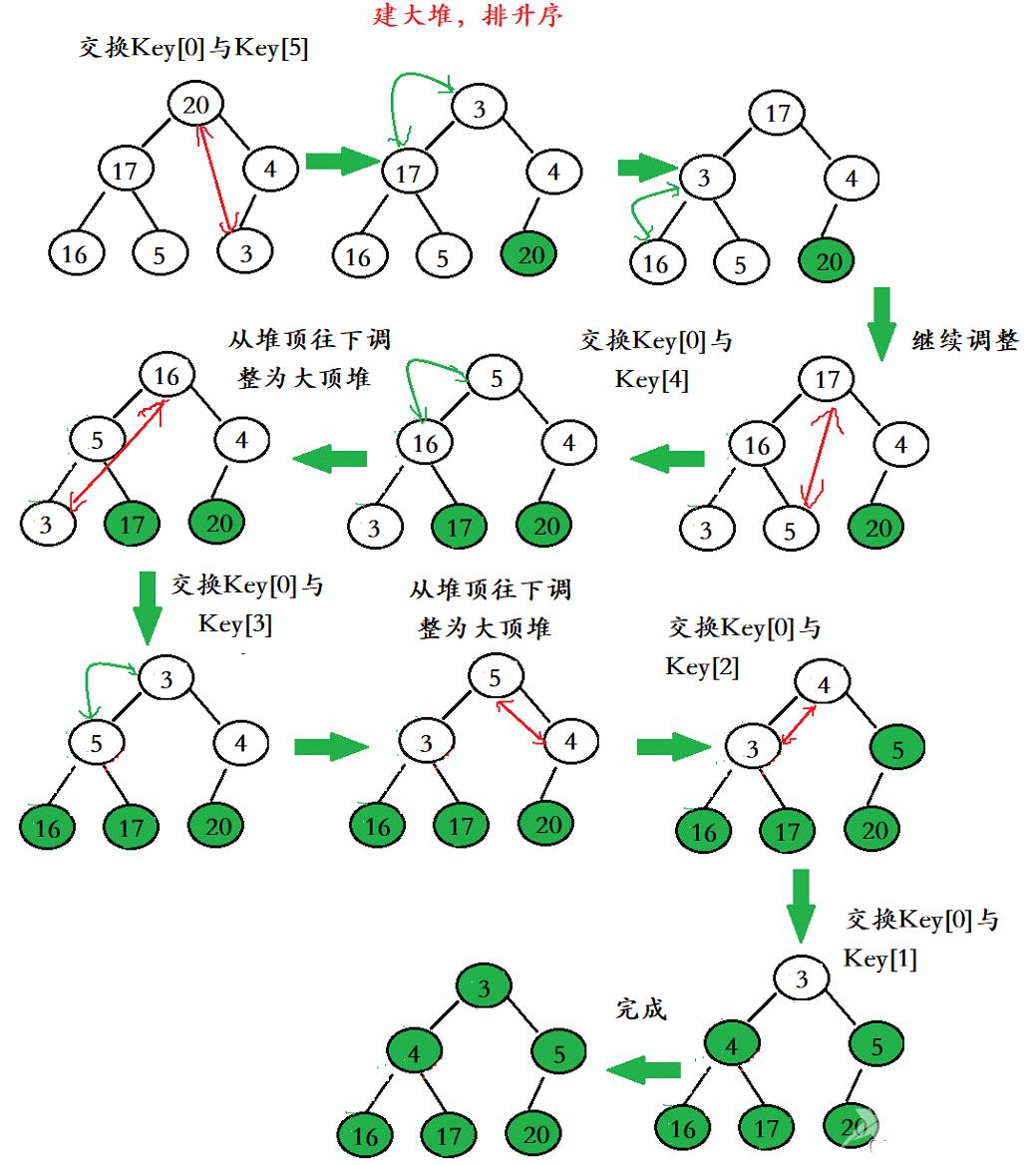
2.5 代码实现
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
//打印数据
void Printf(int* a, int n)
{
for (int i = 0; i < n; ++i)
{
printf("%d ", a[i]);
}
}
//交换,传地址
void Swap(int* child, int* parent)
{
int tmp = *child;
*child = *parent;
*parent = tmp;
}
//向下调整算法
//从根节点开始,如果是建立小堆选出左右孩子中小的那一个,跟父亲比较,如果比父亲小就交换
void AdjustDwon(int* a, int n, int root)//建小堆
{
int parent = root;//父亲节点
int child = parent * 2 + 1;//默认是左孩子
while (child < n)//叶子节点下标不会超过数组总下标数n
{
//选出左右孩子中最小的那一个
if (child+1 < n&& a[child + 1] < a[child])
{
child += 1;//用a[child]与父亲节点a[parent]比较
}
if (a[child] < a[parent])
{
//交换,传地址
Swap(&a[child], &a[parent]);
//交换后,将child,作为根节点继续向下调整,持续建堆
parent = child;
//新的左孩子
child = parent * 2 + 1;
}
else
{
break;//如果不用交换,直接结束循环
}
}
}
//堆的建立
//大堆要求:树中所有的父亲都>=孩子,根是最大的
//小堆要求:书中所有的父亲都<=孩子,根是最小的
//建大堆排升序,建小堆排降序
//建堆的时间复杂度是O(N);
void HeapSort(int *a,int n)
{
//找父亲节点
for (int i=(n-1-1)/2;i>=0;--i)
{
//向下调整算法
AdjustDwon(a,n,i);
}
//大堆或小堆建立完毕,排序
//用主根节点与最后一个节点交换位置
int end = n - 1;
while (end>0)
{
//交换,传地址
Swap(&a[0],&a[end]);
//继续向下调整
AdjustDwon(a,end,0);
--end;
}
}
//选择排序—堆排序
int main()
{
int a[10] = {9,2,5,4,3,1,6,7,8,0};
//堆的建立
HeapSort(a,sizeof(a) / sizeof(a[0]));
//打印数据
Printf(a,sizeof(a) / sizeof(a[0]));
return 0;
}
2.6 堆排序的特性总结
- 1.堆排序使用堆来选数,效率高很多
- 2.时间复杂度:O(N*logN)
- 3.空间复杂度:O(1)
- 4.稳定性:不稳定
2.7 堆排序的特性总结
- 1.堆排序使用堆来选数,效率高很多
- 2.时间复杂度:O(N*logN)
- 3.空间复杂度:O(1)
- 4.稳定性:不稳定
到此这篇关于C语言排序算法之选择排序(直接选择排序,堆排序)的文章就介绍到这了,更多相关C语言选择排序 内容请搜索自由互联以前的文章或继续浏览下面的相关文章希望大家以后多多支持自由互联!
