【磨刀霍霍向数模】系列之凸优化求解利器cvxpy

CVXPY是Python中内置的解决凸优化问题的模块，其可以自动转化问题为标准形式，调用解法器，求解。

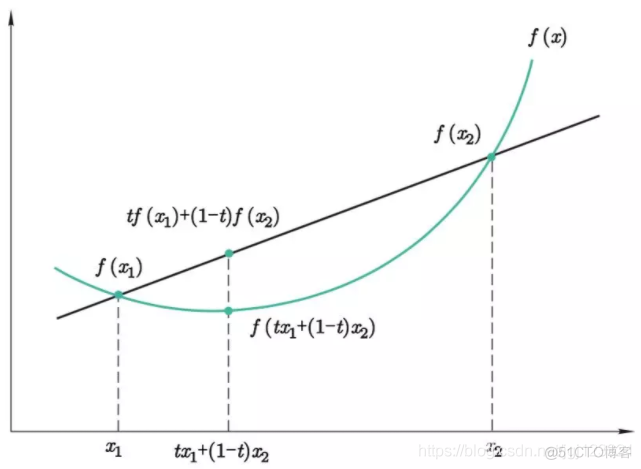
从几何上直观地理解凸函数的特点，即凸函数的割线在函数曲线的上方，如下图所示：

本文介绍求解的常见思路方法。

1. 设定变量

cvx.Variable(shape=(), name=None, var_id=None, **kwargs) # 举例 x=cvx.Variable(shape=(10,3), name='cov', symmetric=True)

• 参数介绍

参数 参数含义 shape 变量的维度, 如使用(10,2) 表示 10 × 2的矩阵 name 变量名 **kwargs 可添加的其他属性：neg （负数），nonneg（非负） 等（需要用字典形式传入，如neg =True）

2. 设定目标函数

可选cvx.Minimize（最大值）或则和cvx.Maximize（最小值）

如：cvx.Minimize(A@x)（A@x表示A点乘x）

3. 求解

• 定义问题

prob=cvx.Problem(obj,cons)

• 求解

prob.solve()

4. 实例

• 求解问题

$min_x\ \ \frac{1}{2}x_1^2 +x_2^2 -x_1x_2-2x_1-6x_2$

$s.t. \ \ \ \ \ \ x_1 +x_2 \leq 2\\ \ \ \ \ \ \ \ -x_1+2x_2\leq2\\ \ \ \ \ \ \ \ \ \ \ 2x_1+x_2\leq3\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0\leq x$

• 求解思路

先将目标函数转化为二次规划问题的一般形式：

$minimize\ \frac{1}{2}x^TPx + q^Tx$

$subject\ to\ \ Gx≤h,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Ax=b$

可得:$P = \begin{bmatrix}1 & -1\-1&2\end{bmatrix}, f' = \begin{bmatrix}-2\-6\end{bmatrix}$

前三个约束条件可以转化为：$A = \begin{bmatrix}1&1\-1&2\2&1\\end{bmatrix}$然后求解即可。

• 完整代码

# 导入库 import numpy as np import cvxpy as cvx # 变量个数 x = cvx.Variable(2) # 二次规划目标函数中的参数 P = np.array([[1, -1], [-1, 2]]) f = np.array([-2, -6]) # 约束条件左侧 A = np.array([[1, -1], [-1, 2], [2, 1]]) # 约束条件右侧 b = np.array([2, 2, 3]) # 完整的目标函数 obj = cvx.Minimize((1/2)*cvx.quad_form(x, P)+f.T@x) # 完整的约束条件（用list形式） cons = [A@x <= b, x >= 0] # 求解 prob = cvx.Problem(obj, cons) prob.solve() # 输出结果 print(prob.status, prob.value, x.value)

• 输出结果

optimal -8.839999999999998 [0.8 1.4]

参考链接：https://aistudio.baidu.com/aistudio/projectdetail/2564143