从真题中理解信道复用技术、最优二叉树[Huffman Tree]
- 题目概述
- 题目解答
- 题目相关知识
- 信道复用技术
- 频分复用 FDM (Frequency Division Multiplexing)
- 时分复用TDM (Time Division Multiplexing) (同步时分复用)
- 统计时分复用 STDM (Statistic TDM) (异步时分复用)
- 波分复用 WDM(Wavelength Division Multiplexing)
- 码分复用 CDM (Code Division Multiplexing)
- 最优二叉树(Huffman Tree)
- 哈夫曼树的构造过程
- 哈夫曼编码
- 参考文献
题目概述
为共享信道，常会使用信道复用技术。同时为了减少信道负担，会采用压缩编码技术。据此，请对下列问题进行作答: 1）请分析同步时分复用与异步时分复用的区别 2）请分析频分复用与波分复用的关联; 3）现有一个由5个不同符号组成的30个符号的字符串L：BABACACADADABBCBABEBEDDABEEEBB 请采用树形结构的最优压缩编码技术对L进行编码; 4）并计算压缩后的平均码长与压缩比的实际值。
题目解答
1）区别：
- （1）同步时分复用，指的是将一个帧的若干时隙，按顺序编号，标号相同的成为一个子信道，传递同一路话路信息，速率恒定。 固定分配带宽，对传递的信号无差别控制，并且不做任何处理，其流量控制基于呼叫延时制。同步时分多路复用技术优点是控制简单，实现起来容易。缺点是如果某路信号没有足够多的数据，不能有效地使用它的时间片，则造成资源的浪费；而有大量数据要发送的信道又由于没有足够多的时间片可利用，所以要拖很长一段的时间，降低了设备的利用效率。
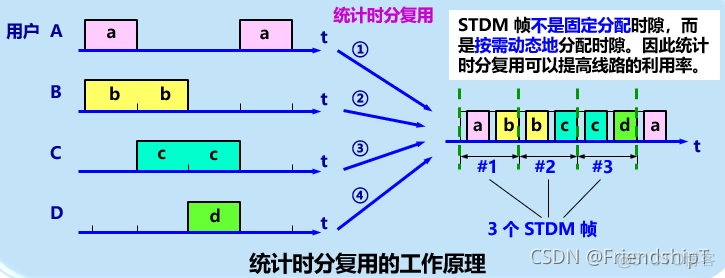
- （2）异步时分复用，也叫做统计时分复用。指的是将用户的数据划分为一个个数据单元，不同用户的数据单元仍按照时分的方式来共享信道；但是不再使用物理特性来标识不同用户，而是使用数据单元中的若干比特，也就是使用逻辑的方式来标识用户。这种方法提高了设备利用率，但是技术复杂性也比较高，所以这种方法主要应用于高速远程通信过程中，例如，异步传输模式ATM。
2）关联：
- 频分复用(FDM，Frequency Division Multiplexing)就是将用于传输信道的总带宽划分成若干个子频带（或称子信道），每一个子信道传输1路信号。频分复用要求总频率宽度大于各个子信道频率之和，同时为了保证各子信道中所传输的信号互不干扰，应在各子信道之间设立隔离带，这样就保证了各路信号互不干扰（条件之一）。频分复用技术的特点是所有子信道传输的信号以并行的方式工作，每一路信号传输时可不考虑传输时延，因而频分复用技术取得了非常广泛的应用。频分复用技术除传统意义上的频分复用(FDM)外，还有一种是正交频分复用(OFDM)。
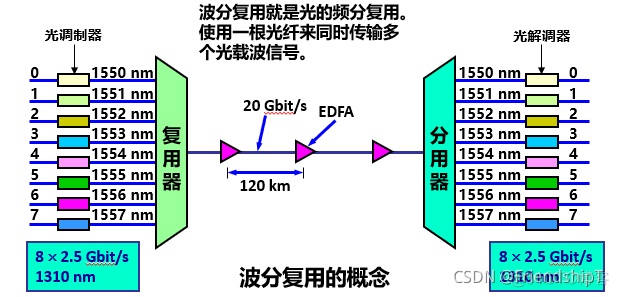
- 波分复用 WDM (Wavelength Division Multiplexing)就是光的频分复用。其是将两种或多种不同波长的光载波信号（携带各种信息）在发送端经复用器(亦称合波器，Multiplexer)汇合在一起，并耦合到光线路的同一根光纤中进行传输的技术；在接收端，经解复用器(亦称分波器或称去复用器，Demultiplexer)将各种波长的光载波分离，然后由光接收机作进一步处理以恢复原信号。这种在同一根光纤中同时传输两个或众多不同波长光信号的技术，称为波分复用。
3） 不同符号出现的次数，如下表。
符号
总数
A
8
B
10
C
3
D
4
E
5
构建的哈夫曼树，如下图。
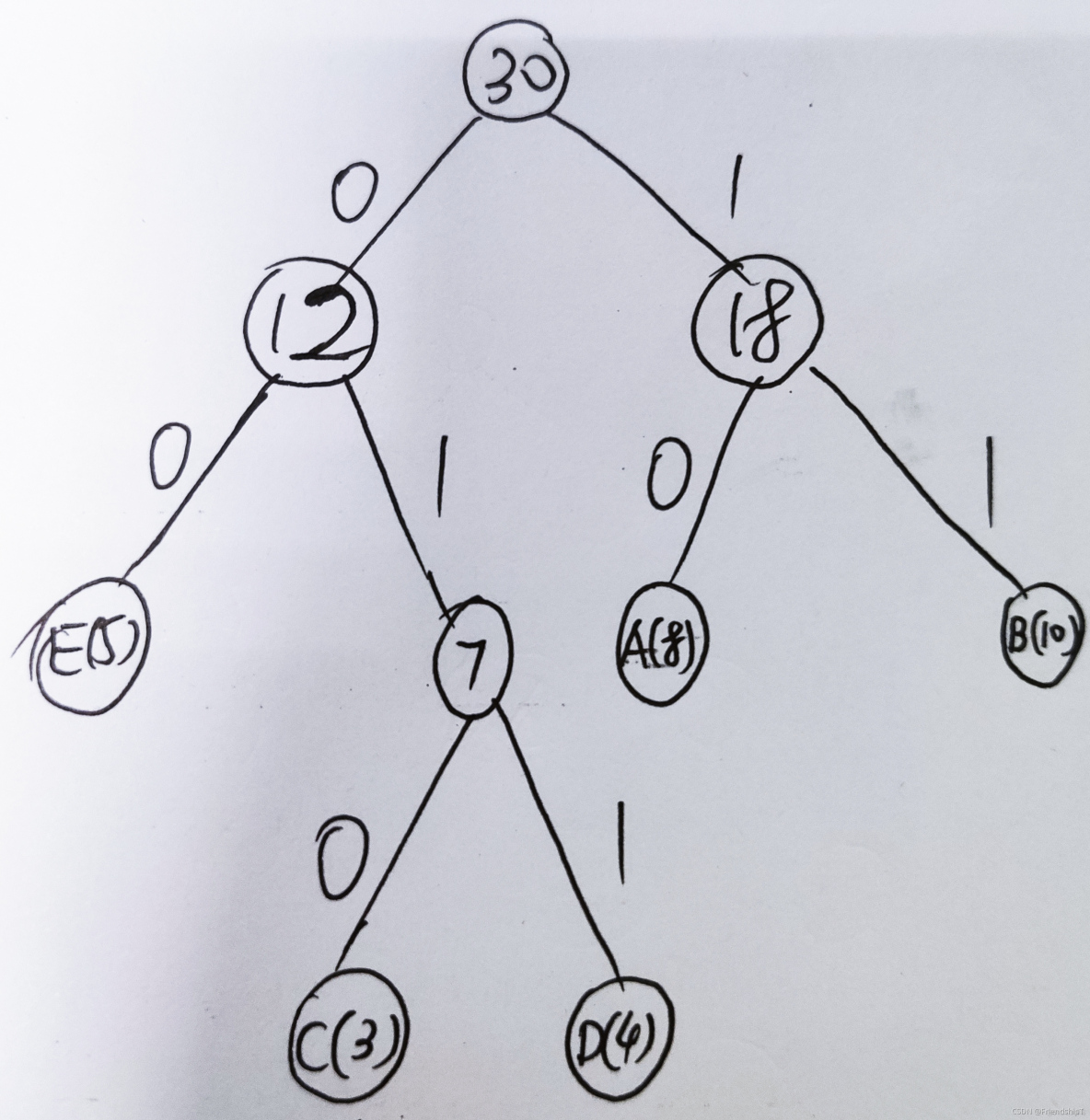
注：符号(总数)
符号
对应的代码
A
10
B
11
C
010
D
011
E
00
符号
总数
对应的代码
所需位数
A
8
10
2*8=16
B
10
11
2*10=20
C
3
010
3*3=9
D
4
011
3*4=12
E
5
00
2*5=10
合计
30
67
注：
- 压缩后的平均码长
- 压缩比的实际值
题目相关知识
信道复用技术
频分复用 FDM (Frequency Division Multiplexing)
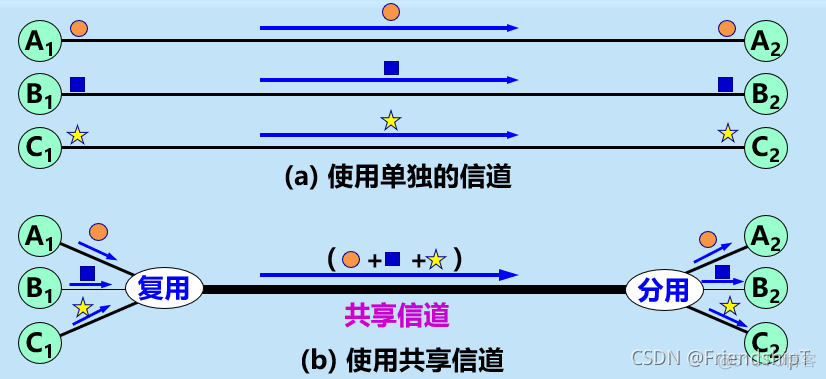
- 将整个带宽分为多份，用户在分配到一定的频带后，在通信过程中自始至终都占用这个频带。
- 频分复用的所有用户在同样的时间占用不同的带宽资源（请注意，这里的“带宽”是频率带宽而不是数据的发送速率）。
时分复用TDM (Time Division Multiplexing) (同步时分复用)
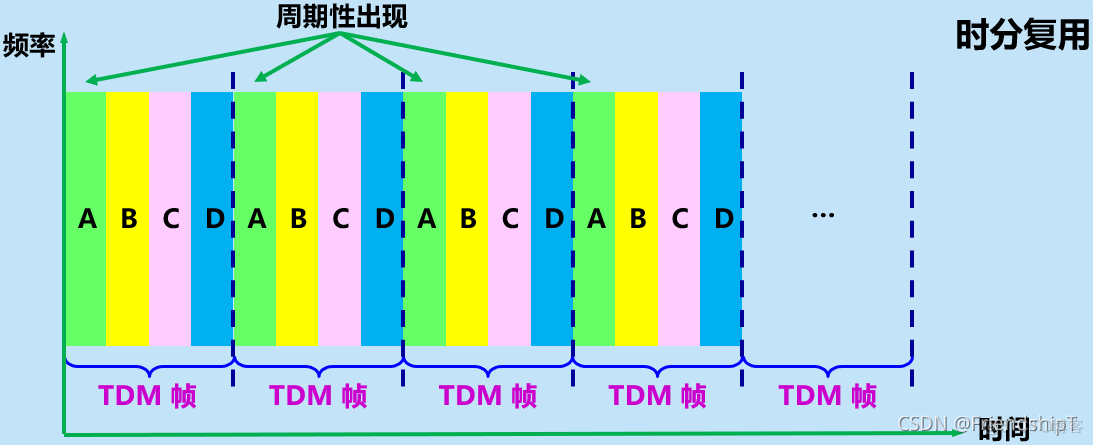
- 时分复用则是将时间划分为一段段等长的时分复用帧（TDM帧）。每一个时分复用的用户在每一个 TDM 帧中占用固定序号的时隙。
- 每一个用户所占用的时隙是周期性地出现（其周期就是TDM帧的长度）的。
- TDM 信号也称为等时 (isochronous) 信号。
- 时分复用的所有用户在不同的时间占用同样的频带宽度。
- 时分复用可能会造成线路资源的浪费
- 使用时分复用系统传送计算机数据时，由于计算机数据的突发性质，用户对分配到的子信道的利用率一般是不高的。
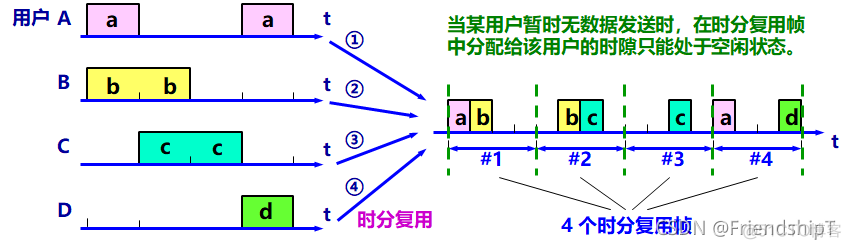
统计时分复用 STDM (Statistic TDM) (异步时分复用)
波分复用 WDM(Wavelength Division Multiplexing)
码分复用 CDM (Code Division Multiplexing)
- 常用的名词是码分多址 CDMA (Code Division Multiple Access)。
- 各用户使用经过特殊挑选的不同码型，因此彼此不会造成干扰。
- 这种系统发送的信号有很强的抗干扰能力，其频谱类似于白噪声，不易被敌人发现。
最优二叉树(Huffman Tree)
给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。
哈夫曼(Huffman)树又称最优树，是一类带权路径长度最短的树，在实际中有广泛的用途。哈夫曼树的定义，涉及路径、路径长度、权等概念。
- (1)路径：从树中 一 个结点到另 一 个结点之间的分支构成这两个结点之间的路径。
- (2)路径长度：路径上的分支数目称作路径长度。
- (3)树的路径长度：从树根到每 一 结点的路径长度之和。
- (4)权：赋予某个实体的 一 个量，是对实体的某个或某些属性的数值化描述。 在数据结构中，实体有结点（元素）和边（关系）两大类，所以对应有结点权和边权。 结点权或边权具体代表什么意义，由具体情况决定。如果在 一 棵树中的结点上带有权值，则对应的就有带权树等概念。
- (5)结点的带权路径长度：从该结点到树根之间的路径长度与结点上权的乘积。
- (6)树的带权路径长度：树中所有叶子结点的带权路径长度之和，通常记作
- (7)哈夫曼树：假设有m个权值
其中以( C )树的为最小。可以验证，它恰为哈夫曼树，即其带权路径长度在所有带权为 7、 5、2 、4的4个叶子结点的二叉树中居最小。
哈夫曼树的构造过程
，构造n棵只有根结点的二叉树，这n棵二叉树构成一个森林F。
哈夫曼树构造过程
哈夫曼编码
在进行数据压缩时，为了使压缩后的数据文件尽可能短， 可采用不定长编码。 其基本思想是：为出现次数较多的字符编以较短的编码。为确保对数据文件进行有效的压缩和对压缩文件进行正确的解码， 可以利用哈夫曼树来设计二进制编码。
- 前缀编码：如果在一个编码方案中，任一个编码都不是其他任何编码的前缀(最左子串),则称编码是前缀编码。
- 哈夫曼编码：对一棵具有n个叶子的哈夫曼树，若对树中的每个左分支赋予0, 右分支赋予1则从根到每个叶子的路径上，各分支的赋值分别构成一个二进制串， 该二进制串就称为哈夫曼编码。
- 哈夫曼编码是前缀编码。
- 哈夫曼编码是最优前缀编码。
参考文献
[1] 谢希仁. 计算机网络. 7版. 北京：电子工业出版社，2017 [2] 严蔚敏，吴伟民. 数据结构（C语言版）. 北京： 清华大学出版社，2020 [3] 王道论坛. 2022数据结构考研复习指导. 北京：电子工业出版社，2021 [4] 王道论坛. 2022计算机网络考研复习指导. 北京：电子工业出版社，2021