一、平衡二叉树
平衡二叉树 也称平衡二叉搜索树(Self-balancing binary search tree)是一种结构平衡的二分搜索树。
平衡二叉树由二分搜索树发展而来,在二分搜索树的基础上平衡二叉树需要满足两个条件:
- 1、它的左右两个子树的高度差的绝对值不超过1。
- 2、左右两个子树都是一棵平衡二叉树
平衡因子
某结点的左子树与右子树的高度(深度)差即为该结点的平衡因子(BF,Balance Factor)。平衡二叉树上所有结点的平衡因子只可能是 -1,0 或 1。如果某一结点的平衡因子绝对值大于1则说明此树不是平衡二叉树。为了方便计算每一结点的平衡因子我们可以为每个节点赋予height这一属性,表示此节点的高度。
常见的平衡二叉搜索树有:
- AVL树
- 红黑树
- Treap
二、AVL树
AVL树 是由 G. M. Adelson- V elsky 和 E. M. Landis于1962年提出。AVL树是最早的平衡二叉树。
AVL树维护自身的平衡涉及到两个概念:
- 1、节点的高度
- 2、节点的平衡因子
节点的高度就是从根节点到该节点的边的总和
节点的 平衡因子 是左子树的高度减去它的右子树的高度
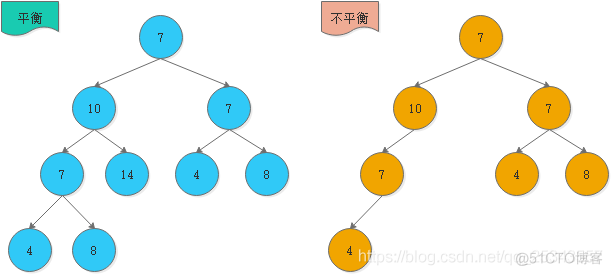
带有平衡因子1、0或 -1的节点被认为是平衡的,因为它的左右子树高度差不超过 1。

面的两张图片,左边的是AVL树,它的任何节点的两个子树的高度差别都<=1;而右边的不是AVL树,因为7的两颗子树的高度相差为2(以2为根节点的树的高度是3,而以8为根节点的树的高度是1)。
三、AVL树代码实现
3.1 基础设计
首先我们可以设计出AVL树节点,并且实现一些简单通用的方法供后续操作。
public class AVLTree<K extends Comparable<K>, V> { //AVLTree 树节点类 private class Node<K extends Comparable<K>, V>{ public K key; public V value; public Node<K, V> left; public Node<K, V> right; //当前节点所处的高度值 public int height; public Node(K key, V value){ this.key = key; this.value = value; this.left = null; this.right = null; //初始化新的节点都是叶子节点,高度都为1 this.height = 1; } @Override public String toString() { return key.toString() +" : " + value.toString(); } } // 根节点 private Node<K, V> root; // 树容量 private Integer size; public AVLTree(){ root = null; size = 0; } public boolean isEmpty() { return size == 0; } public int getSize() { return size; } /** * 判断该二叉树是否是一棵平衡二叉树 * @return */ private boolean isBalanced(){ return isBalanced(root); } /** * 判断该二叉树是否是一棵平衡二叉树, 递归调用函数 * @param node * @return */ private boolean isBalanced(Node<K,V> node){ //node == null 代表该树是一颗平衡二叉树, //平衡二叉树左右子树高度相差不超过1 // 因为空树的左右子树高度相差不超过1 if(node == null){ return true; } //获取平衡因子 int balanceFactor = getBalanceFactor(node); //左右子树高度相差超过1,则不是平衡二叉树 if(Math.abs(balanceFactor) > 1){ return false; } //递归调用该节点的左右子树,判断是否是平衡二叉树 return isBalanced(node.left) && isBalanced(node.right); } /** * 返回node节点的高度值 * @param node * @return */ private int getHeight(Node<K, V> node){ if(node == null){ return 0; } return node.height; } /** * 获取节点node的平衡因子 * @param node * @return */ private int getBalanceFactor(Node<K, V> node){ if(node == null){ return 0; } return getHeight(node.left) - getHeight(node.right); } }3.2 添加节点
往平衡二叉树中添加节点很可能会导致二叉树失去平衡,所以我们需要在每次插入节点后进行平衡的维护操作。插入节点破坏平衡性有如下四种情况:
3.2.1 LL(右旋)
LL的意思是向左子树(L)的左孩子(L)中插入新节点后导致不平衡,这种情况下需要右旋操作,而不是说LL的意思是右旋,后面的也是一样。
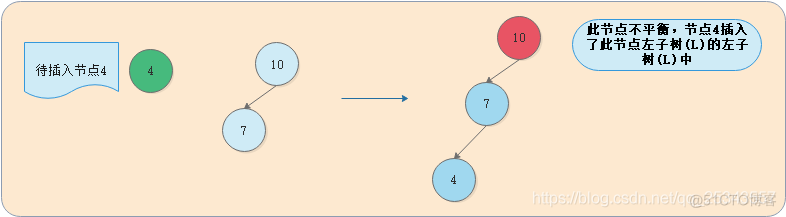
我们将这种情况抽象出来,得到下图:
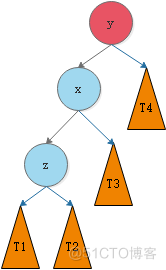
我们需要对节点y进行平衡的维护。步骤如下图所示:
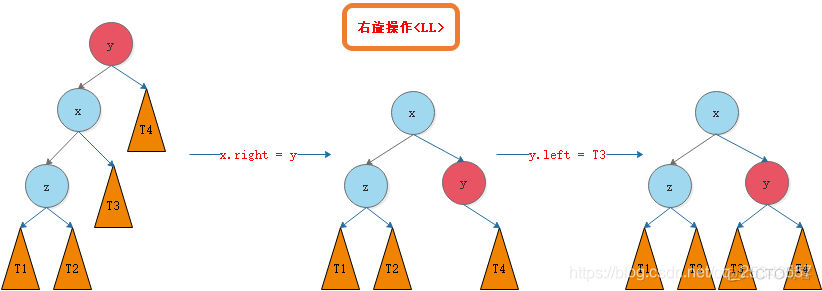
3.2.2 RR(左旋)
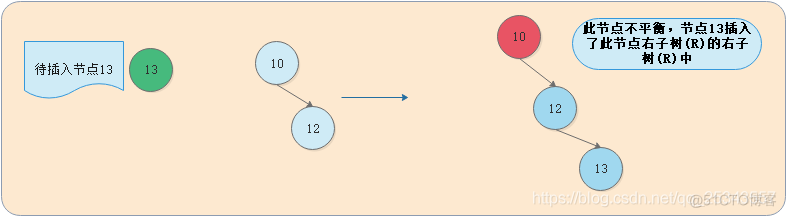
我们将这种情况抽象出来,得到下图:
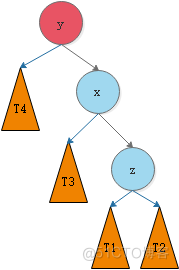
我们需要对节点y进行平衡的维护。步骤如下图所示:
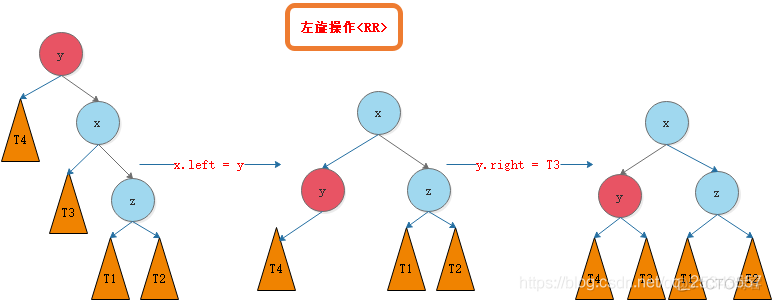
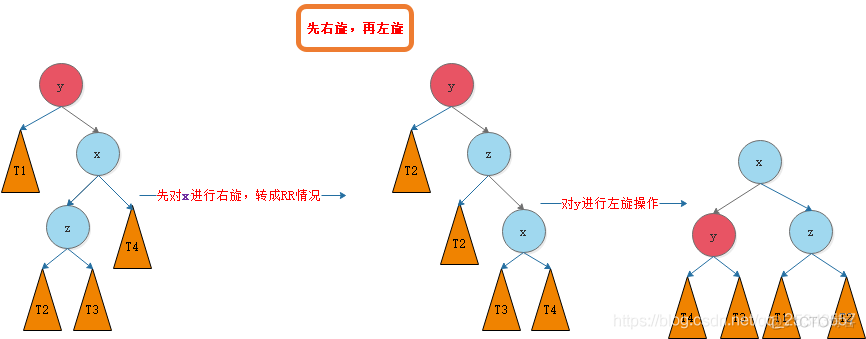
3.2.3 LR
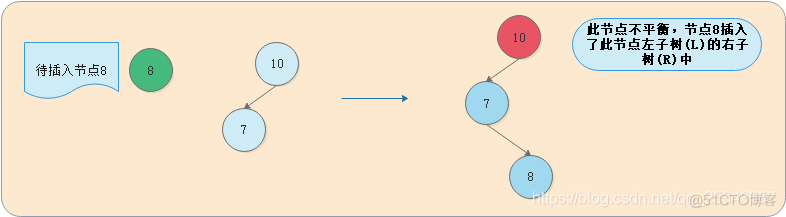
我们将这种情况抽象出来,得到下图:
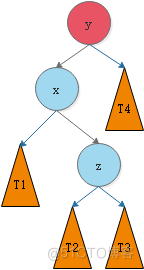
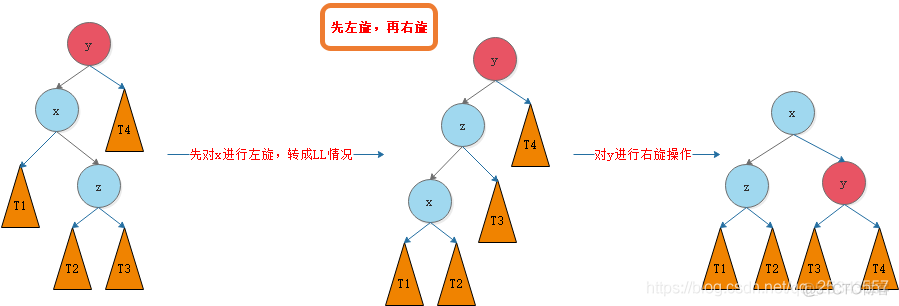
我们需要对节点y进行平衡的维护。步骤如下图所示:
3.2.4 RL
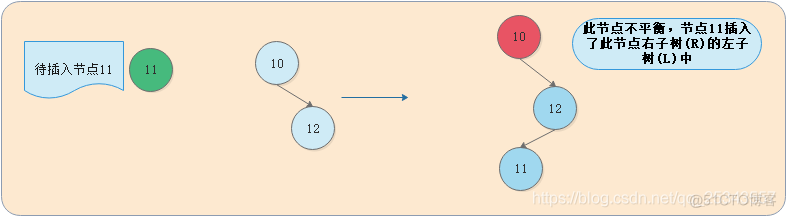
我们将这种情况抽象出来,得到下图:
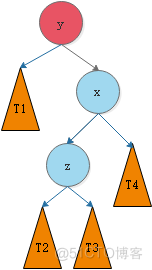
我们需要对节点y进行平衡的维护。步骤如下图所示:
添加节点代码
/** * 向AVL树添加新的元素(key,value) * @param key * @param value */ public void add(K key, V value){ //向根节点添加元素e root = add(root, key, value); } /** * 向以node为根的AVL树中插入元素(key,value),递归算法 * @param node * @param key * @param value * @return 返回插入新元素的AVL树的根 */ private Node<K, V> add(Node<K, V> node, K key, V value){ if(node == null){ size ++; return new Node<>(key, value); } //递归调用,元素添加到node.left if(key.compareTo(node.key) < 0){ node.left = add(node.left, key, value); }else if(key.compareTo(node.key) > 0){ //递归调用,元素添加到node.right node.right = add(node.right, key, value); }else { node.value = value; } //更新节点的高度height node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1; //计算平衡因子 int balanceFactor = getBalanceFactor(node); //平衡维护 //LL // 左子树比右子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在左子树的左子树的左侧 if(balanceFactor > 1 && getBalanceFactor(node.left) >= 0){ //右旋转 return rightRotate(node); } //RR // 右子树比左子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在右子树的右子树的右侧 if(balanceFactor < -1 && getBalanceFactor(node.right) <= 0){ //左旋转 return leftRotate(node); } //LR // 左子树比右子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在左子树的左子树的右侧 if(balanceFactor > 1 && getBalanceFactor(node.left) < 0){ //先对node.left进行左旋转 node.left = leftRotate(node.left); //然后对node进行右旋转 return rightRotate(node); } //RL // 右子树比左子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在右子树的右子树的左侧 if(balanceFactor < -1 && getBalanceFactor(node.right) > 0){ //先对node.right进行右旋转 node.right = rightRotate(node.right); //然后对node进行左旋转 return leftRotate(node); } //返回当前根节点 return node; }3.3 删除节点
在删除AVL树节点前需要知道二分搜索树的节点删除操作,和二分搜索树删除节点不同的是我们删除AVL树的节点后需要进行平衡的维护操作。
/** * 返回以node为根的二分搜索树的最小值所在的节点 * @param node * @return */ private Node<K, V> minimum(Node<K, V> node){ if(node.left == null){ return node; } return minimum(node.left); } /** * 从二分搜索树中删除元素键为key的节点, 并返回value, 不存在返回null * @param key * @return */ public V remove(K key){ Node<K, V> node = getNode(root, key); if(node == null){ //不存在直接返回null return null; } //存在 root = remove(root, key); return node.value; } /** * 删除以node为根的二分搜索树中键为key的节点,递归递归方式 * 返回删除节点后新的二分搜索树的根 * @param node * @param key * @return */ private Node<K, V> remove(Node<K, V> node, K key){ //节点为空,直接返回 if(node == null){ return null; } //声明要返回去的node Node<K, V> retNode; if(key.compareTo(node.key) < 0){ //待删除元素key小于当前节点的键,向左递归寻找 node.left = remove(node.left, key); retNode = node; }else if(key.compareTo(node.key) > 0){ //待删除元素key大于当前节点的键,向右递归寻找 node.right = remove(node.right, key); retNode = node; }else { //待删除节点左子树为空 if(node.left == null){ Node<K, V> rightNode = node.right; node.right = null; size --; retNode = rightNode; } //待删除节点右子树为空 else if(node.right == null){ Node<K, V> rightNode = node.left; node.left = null; size --; retNode = rightNode; }else { //待删除节点左、右子树不为空 //找到比待删除节点大的最小节点,即待删除节点右子树最小节点 //用这个节点顶替待删除节点的位置 //找到比待删除节点大的最小节点,即待删除节点右子树最小节点 Node<K, V> successor = minimum(node.right); //删除比待删除节点大的最小节点,并将返回值给succeer的右孩子 //successor.right = removeMin(node.right); successor.right = remove(node.right, successor.key); //node.left赋值给successor.left successor.left = node.left; //node节点和二分搜索树脱离关系 node.left = node.right = null; retNode = successor; } } if(retNode == null){ //如果删除了该节点,返回的二叉树节点的根节点为空的话 return null; } //更新节点的高度height retNode.height = Math.max(getHeight(retNode.left), getHeight(retNode.right)) + 1; //计算平衡因子 int balanceFactor = getBalanceFactor(retNode); //平衡维护 //LL // 左子树比右子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在左子树的左子树的左侧 if(balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0){ //右旋转 return rightRotate(retNode); } //RR // 右子树比左子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在右子树的右子树的右侧 if(balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0){ //左旋转 return leftRotate(retNode); } //LR // 左子树比右子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在左子树的左子树的右侧 if(balanceFactor > 1 && getBalanceFactor(retNode.left) < 0){ //先对node.left进行左旋转 retNode.left = leftRotate(retNode.left); //然后对node进行右旋转 return rightRotate(retNode); } //RL // 右子树比左子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在右子树的右子树的左侧 if(balanceFactor < -1 && getBalanceFactor(retNode.right) > 0){ //先对node.right进行右旋转 retNode.right = rightRotate(retNode.right); //然后对node进行左旋转 return leftRotate(retNode); } //如果删除节点后,没有打破平衡,直接返回当前根节点 return retNode; }3.4 完整代码
import java.util.ArrayList; import java.util.List; /** * @Author: huangyibo * @Date: 2022/2/26 20:24 * @Description: AVL Tree */ public class AVLTree<K extends Comparable<K>, V> { //AVLTree 树节点类 private class Node<K extends Comparable<K>, V>{ public K key; public V value; public Node<K, V> left; public Node<K, V> right; //当前节点所处的高度值 public int height; public Node(K key, V value){ this.key = key; this.value = value; this.left = null; this.right = null; //初始化新的节点都是叶子节点,高度都为1 this.height = 1; } @Override public String toString() { return key.toString() +" : " + value.toString(); } } // 根节点 private Node<K, V> root; // 树容量 private Integer size; public AVLTree(){ root = null; size = 0; } public boolean isEmpty() { return size == 0; } public int getSize() { return size; } /** * 判断该二叉树是否是一棵二分搜索树 * @return */ private boolean isBST(){ List<K> keys = new ArrayList<>(); inOrder(root, keys); for (int i = 1; i < keys.size(); i++) { if(keys.get(i - 1).compareTo(keys.get(i)) > 0){ return false; } } return true; } //中序遍历 private void inOrder(Node<K,V> node, List<K> keys) { if(node == null){ return; } inOrder(node.left, keys); keys.add(node.key); inOrder(node.right, keys); } /** * 判断该二叉树是否是一棵平衡二叉树 * @return */ private boolean isBalanced(){ return isBalanced(root); } /** * 判断该二叉树是否是一棵平衡二叉树, 递归调用函数 * @param node * @return */ private boolean isBalanced(Node<K,V> node){ //node == null 代表该树是一颗平衡二叉树, //平衡二叉树左右子树高度相差不超过1 // 因为空树的左右子树高度相差不超过1 if(node == null){ return true; } //获取平衡因子 int balanceFactor = getBalanceFactor(node); //左右子树高度相差超过1,则不是平衡二叉树 if(Math.abs(balanceFactor) > 1){ return false; } //递归调用该节点的左右子树,判断是否是平衡二叉树 return isBalanced(node.left) && isBalanced(node.right); } /** * 返回node节点的高度值 * @param node * @return */ private int getHeight(Node<K, V> node){ if(node == null){ return 0; } return node.height; } /** * 获取节点node的平衡因子 * @param node * @return */ private int getBalanceFactor(Node<K, V> node){ if(node == null){ return 0; } return getHeight(node.left) - getHeight(node.right); } /** * 右旋转 * // 对节点y进行向右旋转操作,返回旋转后新的根节点x * // y x * // / \ / \ * // x T4 向右旋转 (y) z y * // / \ - - - - - - - -> / \ / \ * // z T3 T1 T2 T3 T4 * // / \ * // T1 T2 * @param y * @return */ private Node<K, V> rightRotate(Node<K, V> y){ Node<K, V> x = y.left; Node<K, V> T3 = x.right; //向右旋转过程 x.right = y; y.left = T3; //更新节点的高度height值 y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1; x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1; return x; } /** * 向左旋转 * // 对节点y进行向左旋转操作,返回旋转后新的根节点x * // y x * // / \ / \ * // T1 x 向左旋转 (y) y z * // / \ - - - - - - - -> / \ / \ * // T2 z T1 T2 T3 T4 * // / \ * // T3 T4 * @param y * @return */ private Node<K, V> leftRotate(Node<K, V> y){ Node<K, V> x = y.right; Node<K, V> T2 = x.left; //向左旋转过程 x.left = y; y.right = T2; //更新节点的高度height值 y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1; x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1; return x; } /** * 向AVL树添加新的元素(key,value) * @param key * @param value */ public void add(K key, V value){ //向根节点添加元素e root = add(root, key, value); } /** * 向以node为根的AVL树中插入元素(key,value),递归算法 * @param node * @param key * @param value * @return 返回插入新元素的AVL树的根 */ private Node<K, V> add(Node<K, V> node, K key, V value){ if(node == null){ size ++; return new Node<>(key, value); } //递归调用,元素添加到node.left if(key.compareTo(node.key) < 0){ node.left = add(node.left, key, value); }else if(key.compareTo(node.key) > 0){ //递归调用,元素添加到node.right node.right = add(node.right, key, value); }else { node.value = value; } //更新节点的高度height node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1; //计算平衡因子 int balanceFactor = getBalanceFactor(node); //平衡维护 //LL // 左子树比右子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在左子树的左子树的左侧 if(balanceFactor > 1 && getBalanceFactor(node.left) >= 0){ //右旋转 return rightRotate(node); } //RR // 右子树比左子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在右子树的右子树的右侧 if(balanceFactor < -1 && getBalanceFactor(node.right) <= 0){ //左旋转 return leftRotate(node); } //LR // 左子树比右子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在左子树的左子树的右侧 if(balanceFactor > 1 && getBalanceFactor(node.left) < 0){ //先对node.left进行左旋转 node.left = leftRotate(node.left); //然后对node进行右旋转 return rightRotate(node); } //RL // 右子树比左子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在右子树的右子树的左侧 if(balanceFactor < -1 && getBalanceFactor(node.right) > 0){ //先对node.right进行右旋转 node.right = rightRotate(node.right); //然后对node进行左旋转 return leftRotate(node); } //返回当前根节点 return node; } /** * 根据key从当前以当前node为根节点中寻找value, 不存在返回null * @param node * @param key * @return */ private Node<K, V> getNode(Node<K, V> node, K key){ //递归终止条件 if(node == null){ return null; } //待寻找key比当前节点key小,递归调用node.left if(key.compareTo(node.key) < 0){ return getNode(node.left, key); }else if(key.compareTo(node.key) > 0){ //待寻找key比当前节点key大,递归调用node.right return getNode(node.right, key); }else { //待寻找key和当前节点key相等,直接返回 return node; } } public boolean contains(K key) { return getNode(root, key) != null; } public void set(K key, V value) { Node<K, V> node = getNode(root, key); if(node == null){ //不存在直接抛异常 throw new IllegalArgumentException(key + " doesn't exist!"); } //key已存在,则更新 node.value = value; } public V get(K key) { Node<K, V> node = getNode(root, key); return node == null ? null : node.value; } /** * 返回以node为根的二分搜索树的最小值所在的节点 * @param node * @return */ private Node<K, V> minimum(Node<K, V> node){ if(node.left == null){ return node; } return minimum(node.left); } /** * 从二分搜索树中删除元素键为key的节点, 并返回value, 不存在返回null * @param key * @return */ public V remove(K key){ Node<K, V> node = getNode(root, key); if(node == null){ //不存在直接返回null return null; } //存在 root = remove(root, key); return node.value; } /** * 删除以node为根的二分搜索树中键为key的节点,递归递归方式 * 返回删除节点后新的二分搜索树的根 * @param node * @param key * @return */ private Node<K, V> remove(Node<K, V> node, K key){ //节点为空,直接返回 if(node == null){ return null; } //声明要返回去的node Node<K, V> retNode; if(key.compareTo(node.key) < 0){ //待删除元素key小于当前节点的键,向左递归寻找 node.left = remove(node.left, key); retNode = node; }else if(key.compareTo(node.key) > 0){ //待删除元素key大于当前节点的键,向右递归寻找 node.right = remove(node.right, key); retNode = node; }else { //待删除节点左子树为空 if(node.left == null){ Node<K, V> rightNode = node.right; node.right = null; size --; retNode = rightNode; } //待删除节点右子树为空 else if(node.right == null){ Node<K, V> rightNode = node.left; node.left = null; size --; retNode = rightNode; }else { //待删除节点左、右子树不为空 //找到比待删除节点大的最小节点,即待删除节点右子树最小节点 //用这个节点顶替待删除节点的位置 //找到比待删除节点大的最小节点,即待删除节点右子树最小节点 Node<K, V> successor = minimum(node.right); //删除比待删除节点大的最小节点,并将返回值给succeer的右孩子 //successor.right = removeMin(node.right); successor.right = remove(node.right, successor.key); //node.left赋值给successor.left successor.left = node.left; //node节点和二分搜索树脱离关系 node.left = node.right = null; retNode = successor; } } if(retNode == null){ //如果删除了该节点,返回的二叉树节点的根节点为空的话 return null; } //更新节点的高度height retNode.height = Math.max(getHeight(retNode.left), getHeight(retNode.right)) + 1; //计算平衡因子 int balanceFactor = getBalanceFactor(retNode); //平衡维护 //LL // 左子树比右子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在左子树的左子树的左侧 if(balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0){ //右旋转 return rightRotate(retNode); } //RR // 右子树比左子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在右子树的右子树的右侧 if(balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0){ //左旋转 return leftRotate(retNode); } //LR // 左子树比右子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在左子树的左子树的右侧 if(balanceFactor > 1 && getBalanceFactor(retNode.left) < 0){ //先对node.left进行左旋转 retNode.left = leftRotate(retNode.left); //然后对node进行右旋转 return rightRotate(retNode); } //RL // 右子树比左子树高度超过了1,说明当前节点的平衡被打破 // 且新添加的节点是在右子树的右子树的左侧 if(balanceFactor < -1 && getBalanceFactor(retNode.right) > 0){ //先对node.right进行右旋转 retNode.right = rightRotate(retNode.right); //然后对node进行左旋转 return leftRotate(retNode); } //如果删除节点后,没有打破平衡,直接返回当前根节点 return retNode; } }四、AVL树实现映射(Map)
- Map接口
- AVLTreeMap实现
五、AVL树实现集合(Set)
- 集合(Set)接口
- AVLTreeSet实现
参考: https://chiclaim.blog.csdn.net/article/details/80740418
https://catwing.blog.csdn.net/article/details/89110319
