TypeScript判断对称的二叉树方案详解

目录

• 前言
• 实现思路
• 实现代码
• 示例代码

前言

如果一颗二叉树和它的镜像一样，那么它就是对称的。实现一个函数用于判断一颗二叉树是否对称，你会怎么做？

本文将分享一种解决方案，欢迎各位感兴趣的开发者阅读本文。

实现思路

在上一篇文章二叉树的镜像中我们知道了此问题的解决方案是前序遍历，那么我们可以修改下前序遍历算法，父节点遍历后，先遍历它的右子节点，再遍历它的左子节点，我们把这种算法称为：对称前序遍历

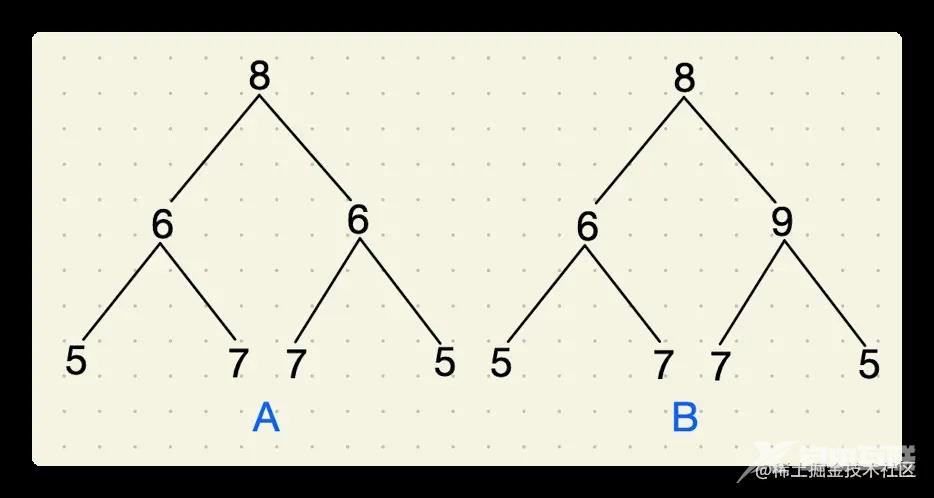
如下图所示的两棵树，我们分别列举下两种遍历的结果：

• 树A：
  • 前序遍历：8, 6, 5, 7, 6, 7, 5
  • 对称前序遍历：8, 6, 5, 7, 6, 7, 5
• 树B：
  • 前序遍历：8, 6, 5, 7, 9, 7, 5
  • 对称前序遍历：8, 9, 5, 7, 6, 7, 5

经过对比后，我们发现树A的两种遍历方法得到的结果是一样的，那么它就是对称的；树B的结果不同，它就不是对称的。

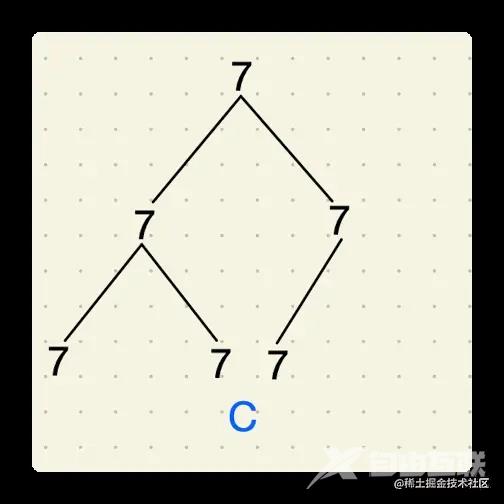
如果有一颗不完全二叉树，它的所有节点都相同，他是对称的吗？

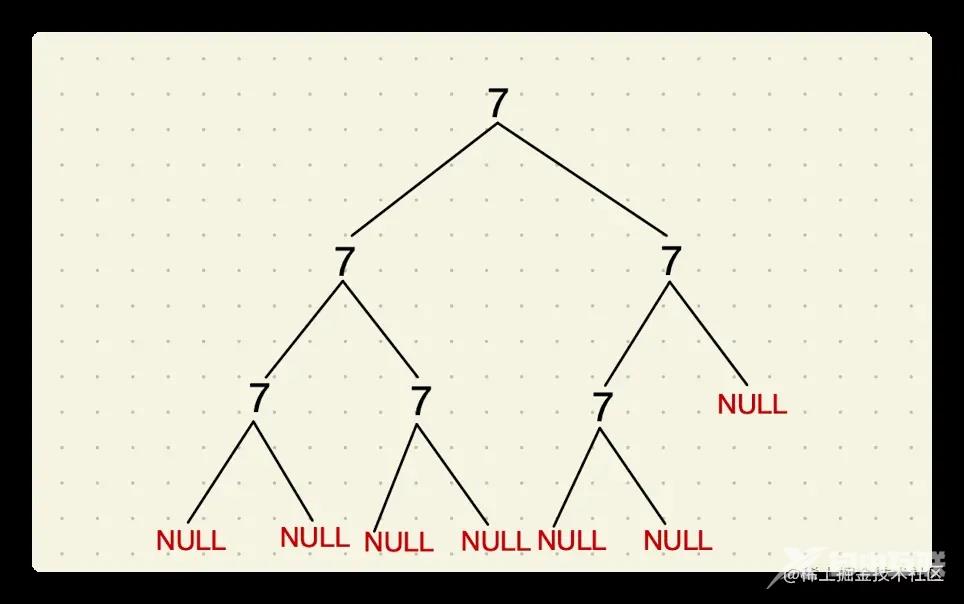
针对于这种情况，我们就需要将它缺省的null节点进行补齐了，补齐后的两种遍历结果为：

• 前序遍历：7, 7, 7, null, null, 7, null, null, 7, 7, null, null, null
• 对称前序遍历：7, 7, null, 7, null, null, 7, 7, null, null, 7, null, null

对比两个结果后，我们发现并不一样，那么它就不是对称的。

实现代码

有了思路后，接下来我们看下代码实现，如下所示：

• 从树的根节点出发，递归比对它的左子节点和右子节点
• 比对过程中：
  • 二者都到达叶子结点，代表这棵树是对称的
  • 任意一方到达叶子结点，代表这棵树不对称
  • 节点值不同，这棵树不对称

export function SymmetricBinaryTree(node: BinaryTreeNode | null): boolean {
  return isSymmetrical(node, node);
}
function isSymmetrical(
  node: BinaryTreeNode | null | undefined,
  cloneNode: BinaryTreeNode | null | undefined
): boolean {
  // 到达叶子节点，两者都为nul代表节点相同
  if (node == null && cloneNode == null) {
    return true;
  }
  // 任意一方到达叶子节点，代表节点不同
  if (node == null || cloneNode == null) {
    return false;
  }
  // 节点值不同
  if (node.key != cloneNode.key) {
    return false;
  }
  // 分别比对树的左子节点和右子节点
  return (
    isSymmetrical(node.left, cloneNode.right) &&
    isSymmetrical(node.right, cloneNode.left)
  );
}

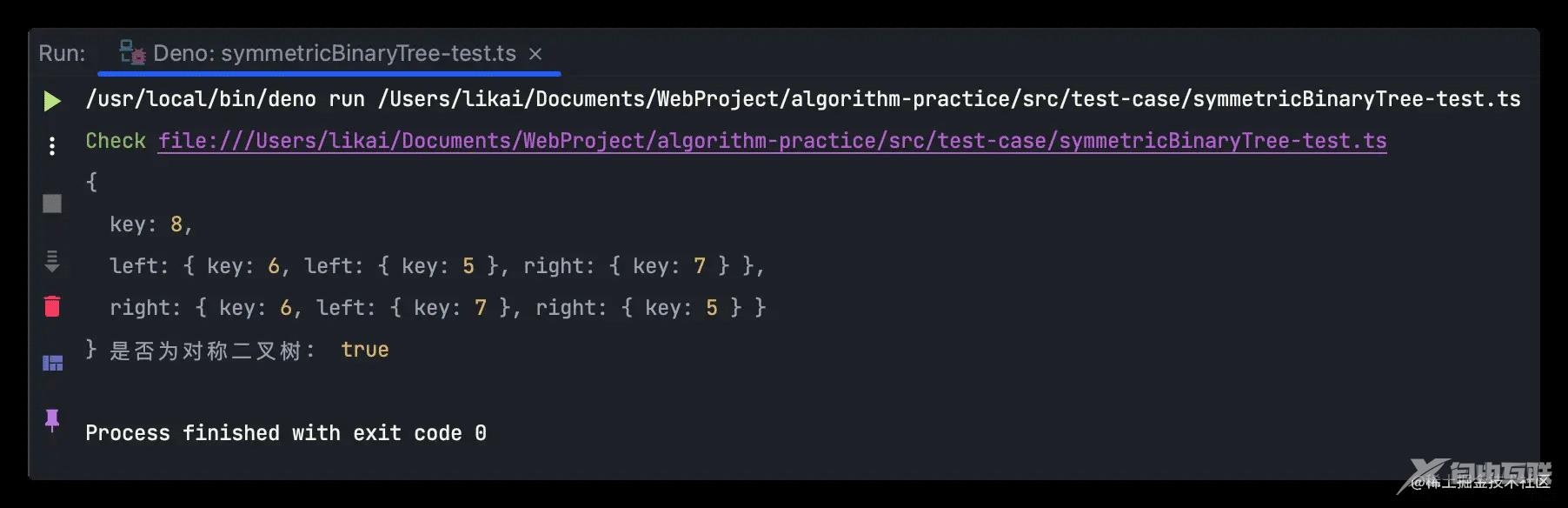
接下来，我们以上个章节列举的例子为例，将其带入上述代码，验证下能否正确判断，如下所示：

const tree: BinaryTreeNode = {
  key: 8,
  left: {
    key: 6,
    left: { key: 5 },
    right: { key: 7 }
  },
  right: { key: 6, left: { key: 7 }, right: { key: 5 } }
};
const isSymmetric = SymmetricBinaryTree(tree);
console.log(tree, "是否为对称二叉树: ", isSymmetric);

示例代码

本文所用代码完整版请移步