求根节点到叶节点数字之和(树、深度优先搜索) 给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。每条从根节点到叶节点的路径都代表一个数字： 例如，从
求根节点到叶节点数字之和(树、深度优先搜索)
给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字：
- 例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1：
输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25
示例 2：
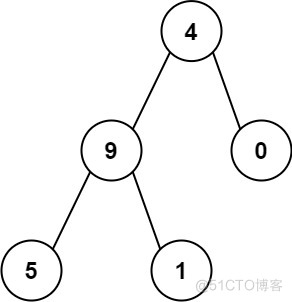
输入：root = [4,9,0,5,1] 输出：1026 解释： 从根到叶子节点路径 4->9->5 代表数字 495 从根到叶子节点路径 4->9->1 代表数字 491 从根到叶子节点路径 4->0 代表数字 40 因此，数字总和 = 495 + 491 + 40 = 1026
提示：
- 树中节点的数目在范围 [1, 1000] 内
- 0 <= Node.val <= 9
- 树的深度不超过 10
解答：
public class Solution { public class TreeNode { int val; TreeNode left; TreeNode right; TreeNode() { } TreeNode(int val) { this.val = val; } TreeNode(int val, TreeNode left, TreeNode right) { this.val = val; this.left = left; this.right = right; } } StringBuffer tempPath = new StringBuffer(); int sum = 0; public void dfs(TreeNode root) { char c = (char) (root.val + '0'); tempPath.append(c); if (root.left == null && root.right == null) { String s = tempPath.toString(); int num = Integer.valueOf(s); sum += num; } if (root.left != null) { dfs(root.left); tempPath.delete(tempPath.length() - 1, tempPath.length()); } if (root.right != null) { dfs(root.right); tempPath.delete(tempPath.length() - 1, tempPath.length()); } } public int sumNumbers(TreeNode root) { dfs(root); return sum; } }二叉树的中序遍历(栈、树)
给定一个二叉树的根节点 root ，返回它的 中序 遍历。
示例 1：
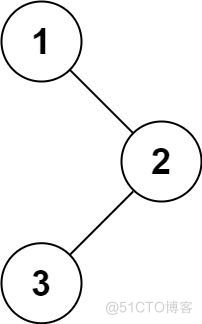
示例 2：
输入：root = [] 输出：[]示例 3：
输入：root = [1] 输出：[1]示例 4：
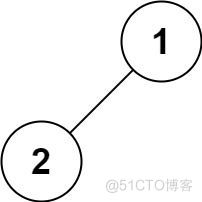
示例 5：
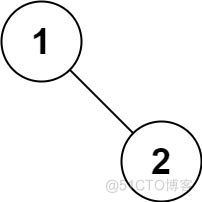
提示：
- 树中节点数目在范围 [0, 100] 内
- -100 <= Node.val <= 100
进阶: 递归算法很简单，你可以通过迭代算法完成吗？
解答：
public class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } } class Solution { public List<Integer> inorderTraversal(TreeNode root) { List<Integer> list = new ArrayList<>(); Stack<TreeNode> stack = new Stack<>(); TreeNode cur = root; while (cur != null || !stack.isEmpty()) { if (cur != null) { stack.push(cur); cur = cur.left; } else { cur = stack.pop(); list.add(cur.val); cur = cur.right; } } return list; } }2 的幂(位运算、递归)
给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。 如果存在一个整数 x 使得 n == 2x ，则认为 n 是 2 的幂次方。
示例 1： 输入：n = 1 输出：true 解释：20 = 1 示例 2： 输入：n = 16 输出：true 解释：24 = 16 示例 3： 输入：n = 3 输出：false 示例 4： 输入：n = 4 输出：true 示例 5： 输入：n = 5 输出：false
提示：
- -231 <= n <= 231 - 1
**进阶：**你能够不使用循环/递归解决此问题吗？
解答：
class Solution { public boolean isPowerOfTwo(int n) { if (n <= 0) return false; return countBit(n) == 1; } public int countBit(int num) { int count = 0; while (num != 0) { count += (num & 1); num >>= 1; } return count; } }本文内容到此结束了， 如有收获欢迎点赞