点上方蓝字计算机视觉联盟获取更多干货
在右上方 ··· 设为星标 ★与你不见不散
仅作学术分享不代表本公众号立场侵权联系删除
转载于机器之心
AI博士笔记系列推荐
周志华《机器学习》手推笔记正式开源可打印版本附pdf下载链接
在本文中来自 MIT 的研究者探讨了关于深度学习中非常基础的问题包括网络的近似能力、优化的动态规律和强泛化能力等。
人工智能AI的复苏很大程度上归功于深度学习在模式识别方面的快速发展。深度神经网络架构的构建一定程度上受到了生物大脑和神经科学的启发。就像生物大脑的内部运行机制一样深度网络在很大程度上无法得到解释没有一个统一的理论。对此来自麻省理工学院MIT的研究者提出了深度学习网络如何运行的新见解有助于人们揭开人工智能机器学习的黑匣子。

论文地址https://cbmm.mit.edu/sites/default/files/publications/PNASlast.pdf
论文作者 Tomaso Poggio、Andrzej Banburski 和 Quianli Liao 来自 MIT 大脑、心智和机器中心Center for Brains, Minds and Machines, CBMM其中 Tomaso Poggio 是 MIT 计算神经学科「大家」也是深度学习理论研究的先锋。他们创建了一种新的理论来解释深度网络的运行原因并于 2020 年 6 月 9 日在 PNAS美国国家科学院院刊上发表了他们的研究成果。

Tomaso Poggio
值得强调的是这篇论文的 editor 是 Stanford 理论大咖 David L. Donoho他的研究方向主要包括谐波分析、信号处理、深度学习以及压缩感知。
研究者重点探究了深度网络对某些类型的多元函数的近似这些函数避免了维数灾难现象即维数准确率与参数量成指数关系。在应用机器学习中数据往往是高维的。高维数据的示例包括面部识别、客户购买历史、病人健康档案以及金融市场分析等。
深度网络的深度是指计算的层数——计算层数越多网络越深。为了阐明自己的理论三位研究者检验了深度学习的近似能力、动态优化以及样本外性能。
深度网络的近似能力
对于一般的范例如下为了确定一个网络的复杂性使用函数 f (x ) 表示理论上应当保证一个未知目标函数 g 的近似达到给定的准确率> 0。特别地深度网络在近似函数方面比浅层网络具备更好的条件。这两种类型的网络都使用相同的操作集——点积、线性组合、单一变量的固定非线性函数、可能的卷积和池化。
如下图 1 所示网络中的每个节点对应于要近似的函数的图中的节点。结果发现深度网络具有比浅层网络更好的近似能力。
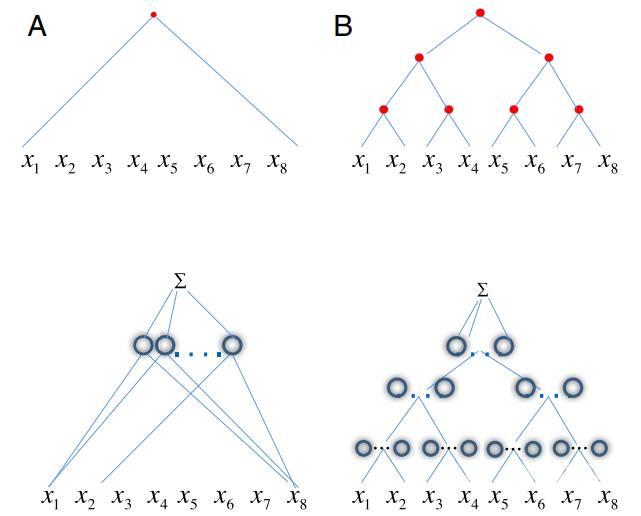
研究者发现通过具有局部层级的深度卷积网络指数成本消失并再次变得更加线性。然后证明了对于特定类型的复合函数卷积深度网络可以避免维数灾难。这意味着对于具有局部层级问题例如图像分类浅层网络与深度网络之间的差距是指数级的。
「在近似理论中无论是浅层网络还是深度网络都在以指数代价近似连续函数然而我们证明了对于某些类型的组合函数卷积型的深度网络即使没有权重共享可以避免维数灾难」研究者表示。
优化的动态规律
之后该团队解释了为什么参数过多的深度网络在样本外数据上表现良好。该研究证明对于分类问题给定一个用梯度下降算法训练的标准深度网络那么重要的是参数空间的方向而不是权重的范数或大小。
参考文献 27 的最新结果说明了在二元分类线性网络的特殊情况下过拟合的明显缺失。他们证明了最小化损失函数如 logistic 函数、交叉熵和指数损失函数等会使线性可分离数据集的最大边值解渐近收敛不受初始条件的影响也不需要显式正则化。这里该研究讨论了非线性多层深度神经网络DNN在指数型损失下的情况如下图 2 所示
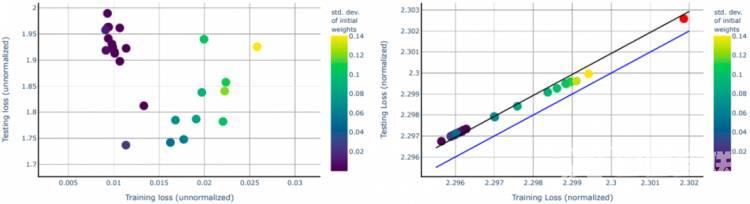
左图显示了在数据集CIFAR-10相同、初始化不同的网络上测试与训练交叉熵损失的对比结果显示在训练集上产生的分类误差为零但测试误差不同右图显示了在相同的数据、相同的网络上测试与训练损失的对比。
研究者这样描述「在描述经验指数损失最小化的特征时我们考虑的是权重方向的梯度流而不是权重本身因为分类的相关函数对应于归一化网络。动态归一化权值与单位范数约束下最小化损失的约束问题等价。特别地典型动态梯度下降与约束问题具有相同的临界点。」
这意味着深度网络上的动态梯度下降与那些对参数的范数和大小都有明确约束的网络等价——梯度下降收敛于最大边值解。研究者发现了线性模型的相似性在这种模型中向量机收敛到伪逆解目的是最小化解的数量。
事实上研究者假定训练深度网络的行为是为了提供隐式正则化和范数控制norm control。科学家们把深度网络的这种能力归因为泛化而无需对正则化项或权重范数进行明确的控制而对于数学计算问题则表明不管在梯度下降中是否存在强制约束单位向量从梯度下降的解中计算保持不变。换言之深度网络选择最小范数解因此具有指数型损失的深度网络的梯度流具有局部最小化期望误差。
「我们认为这项研究结果特别有趣因为它可能解释了深度学习领域出现的最大谜团之一即卷积深度网络在一些感知问题上的不合理有效性」研究者写道。
随着应用数学、统计学、工程学、认知科学以及计算机科学跨学科的交融研究者开发了一种关于为什么深度学习有效的理论它可能会促进新的机器学习技术的发展并在未来加速人工智能的突破。
原文链接https://www.psychologytoday.com/us/blog/the-future-brain/202008/new-ai-study-may-explain-why-deep-learning-works
end
我是王博Kings一名985AI博士在Github上开源了机器学习、深度学习等一系列手推笔记获得了不少同学的支持。
这是我的私人微信还有少量坑位可与相关学者研究人员交流学习
目前开设有人工智能、机器学习、计算机视觉、自动驾驶含SLAM、Python、求职面经、综合交流群扫描添加CV联盟微信拉你进群备注CV联盟

王博的公众号欢迎关注干货多多

王博的系列手推笔记附高清PDF下载
博士笔记 | 周志华《机器学习》手推笔记第一章思维导图
博士笔记 | 周志华《机器学习》手推笔记第二章“模型评估与选择”
博士笔记 | 周志华《机器学习》手推笔记第三章“线性模型”
博士笔记 | 周志华《机器学习》手推笔记第四章“决策树”
博士笔记 | 周志华《机器学习》手推笔记第五章“神经网络”
博士笔记 | 周志华《机器学习》手推笔记第六章支持向量机上
博士笔记 | 周志华《机器学习》手推笔记第六章支持向量机下
博士笔记 | 周志华《机器学习》手推笔记第七章贝叶斯分类上
博士笔记 | 周志华《机器学习》手推笔记第七章贝叶斯分类下
博士笔记 | 周志华《机器学习》手推笔记第八章上
博士笔记 | 周志华《机器学习》手推笔记第八章下
博士笔记 | 周志华《机器学习》手推笔记第九章
点个在看支持一下吧

