作者jostree 转载请注明出处 http://www.cnblogs.com/jostree/p/4098136.html
给定一个非负整数序列$D\{d_1,d_2,...d_n\}$若存在一个无向图使得图中各点的度与此序列一一对应则称此序列可图化。进一步若图为简单图则称此序列可简单图化。
可图化的判定为$d_1d_2 \cdots d_n0(mod2)$。即把奇数度的点配对剩下的变为自环。可简单图化的判定即Havel-Hakimi定理
我们把序列$D$变换为非增序列即$d_1\geq d_2\geq \cdots \geq d_n$则$D$可简单图化当且仅当$D(d_2-1, d_3-1, \cdots ,d_{(d11)}-1, d_{d12}, d_{d13}, \cdots ,d_n)$可简单图化。
证明
<--若$D$可简单图化把原图$G_D$中的最大度点与$G_{D}$中度最大的$d_1$个点连边即可图$G_D$必为简单图。-->若$D$可简单图化设得到的简单图为$D_G$。分两种情况考虑:(a)若$G_D$中存在边$(v_1,v_2), (v_1,v_3), \dots ,(v_1,v_{d_11})$则删除这些边得简单图$G_{D}$于是$D$可简单图化为$G_{D}$
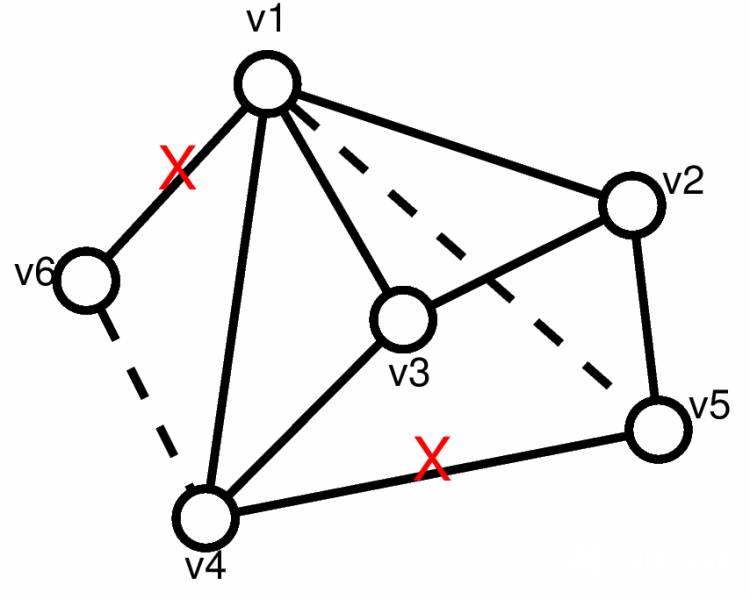
(b)若存在点$v_i,v_j(i 例如对于下图我们删除两条打红X的边添加两条虚线的边即可转化为$G$ 代码实现很简单每次对数组arr排序然后对于arr[1],arr[2],...,arr[arr[0]]每个数减一并另arr[0]0。重复n次最后检验数组是否全部为0是则输出YES和图否则输出NO。 需要注意的是输出格式每两个case之间需要输出一个空行。 代码如下 1 #include 2 #include 3 #include 4 #include 5 #include 6 #define MAXN 11 7 using namespace std; 8 class node 9 {10 public:11 int id;12 int degree;13 bool operator <(const node 16 }17 };18 int n;19 node arr[MAXN];20 int map[MAXN][MAXN];21 void solve()22 {23 memset(map, 0, sizeof(map));24 for( int i 0 ; i 转:https://www.cnblogs.com/jostree/p/4098136.html