前言
卷积和反卷积在CNN中经常被用到想要彻底搞懂并不是那么容易。本文主要分三个部分来讲解卷积和反卷积分别包括概念、工作过程、代码示例其中代码实践部分主结合TensorFlow框架来进行实践。给大家介绍一个卷积过程的可视化工具这个项目是github上面的一个开源项目。 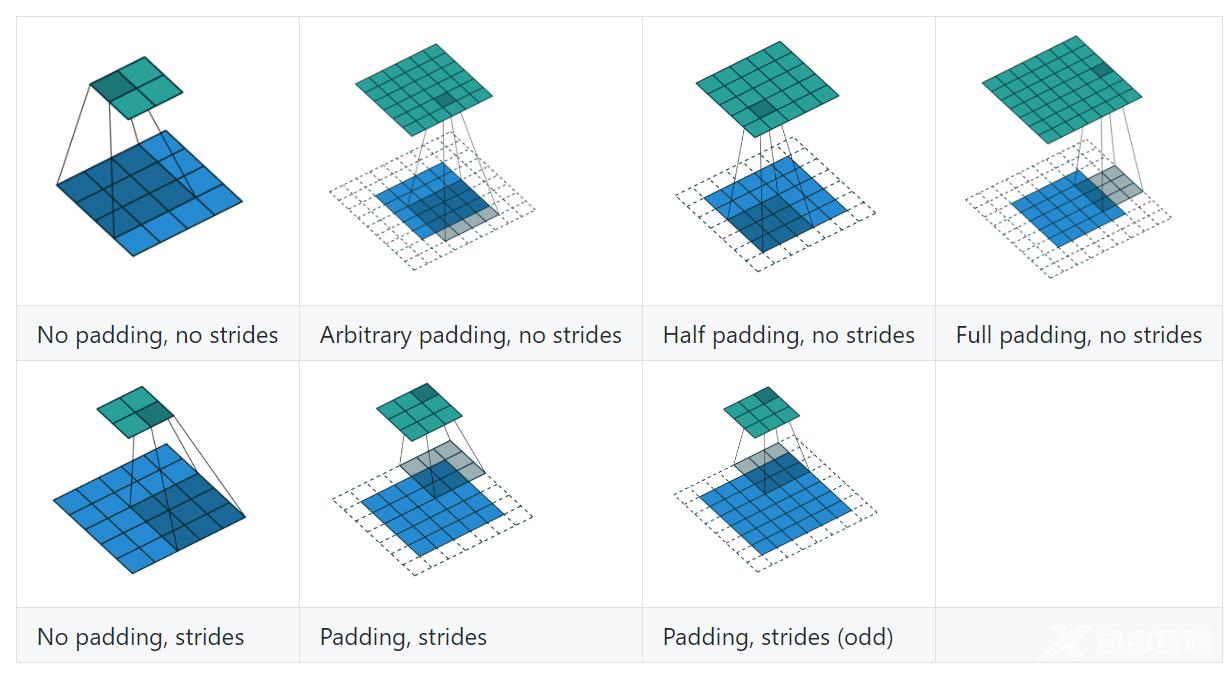
卷积和反卷积
卷积(Convolutional)卷积在图像处理领域被广泛的应用像滤波、边缘检测、图片锐化等都是通过不同的卷积核来实现的。在卷积神经网络中通过卷积操作可以提取图片中的特征低层的卷积层可以提取到图片的一些边缘、线条、角等特征高层的卷积能够从低层的卷积层中学到更复杂的特征从而实现到图片的分类和识别。 反卷积反卷积也被称为转置卷积反卷积其实就是卷积的逆过程。大家可能对于反卷积的认识有一个误区以为通过反卷积就可以获取到经过卷积之前的图片实际上通过反卷积操作并不能还原出卷积之前的图片只能还原出卷积之前图片的尺寸。那么到底反卷积有什么作用呢通过反卷积可以用来可视化卷积的过程反卷积在GAN等领域中有着大量的应用。
工作过程
卷积
 上图展示了一个卷积的过程其中蓝色的图片(4*4)表示的是进行卷积的图片阴影的图片(3*3)表示的是卷积核绿色的图片(2*2)表示是进行卷积计算之后的图片。在卷积操作中有几个比较重要的参数输入图片的尺寸、步长、卷积核的大小、输出图片的尺寸、填充大小。 下面用一个图来详细介绍这些参数
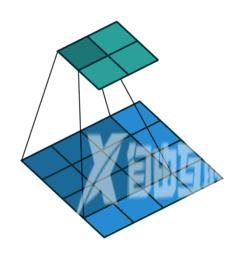
上图展示了一个卷积的过程其中蓝色的图片(4*4)表示的是进行卷积的图片阴影的图片(3*3)表示的是卷积核绿色的图片(2*2)表示是进行卷积计算之后的图片。在卷积操作中有几个比较重要的参数输入图片的尺寸、步长、卷积核的大小、输出图片的尺寸、填充大小。 下面用一个图来详细介绍这些参数  输入图片的尺寸上图中的蓝色图片(55)表示的是需要进行卷积操作的图片在后面的公式中有iiiii iiiik表示卷积核的尺寸。下图展示的是一个padding为VALID的卷积过程卷积核始终都是位于输入矩阵内进行移动。
输入图片的尺寸上图中的蓝色图片(55)表示的是需要进行卷积操作的图片在后面的公式中有iiiii iiiik表示卷积核的尺寸。下图展示的是一个padding为VALID的卷积过程卷积核始终都是位于输入矩阵内进行移动。 
x1 tf.constant(1.0, shape[1,4,4,3])x2 tf.constant(1.0,shape[1,6,6,3])kernel tf.constant(1.0,shape[3,3,3,1])
y1_1 tf.nn.conv2d(x1,kernel,strides[1,2,2,1],padding"SAME")y1_2 tf.nn.conv2d(x1,kernel,strides[1,2,2,1],padding"VALID")y2_1 tf.nn.conv2d(x2,kernel,strides[1,2,2,1],padding"SAME")y2_2 tf.nn.conv2d(x2,kernel,strides[1,2,2,1],padding"VALID")sess tf.InteractiveSession()tf.global_variables_initializer()x1,y1_1,y1_2,x2,y2_1,y2_2 sess.run([x1,y1_1,y1_2,x2,y2_1,y2_2])print(x1.shape) #(1, 4, 4, 3)print(y1_1.shape) #(1, 2, 2, 1)print(y1_2.shape) #(1, 1, 1, 1)print(x2.shape) #(1, 6, 6, 3)print(y2_1.shape) #(1, 3, 3, 1)print(y2_2.shape) #(1, 2, 2, 1)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
下面看一个卷积的计算例子
x1 tf.constant([i*0.1 for i in range(16)],shape[1,4,4,1],dtypetf.float32)kernel tf.ones(shape[3,3,1,1],dtypetf.float32)conv1 tf.nn.conv2d(x1,kernel,strides[1,1,1,1],padding"VALID")sess tf.InteractiveSession()tf.global_variables_initializer()conv1 sess.run(conv1)print(conv1)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9

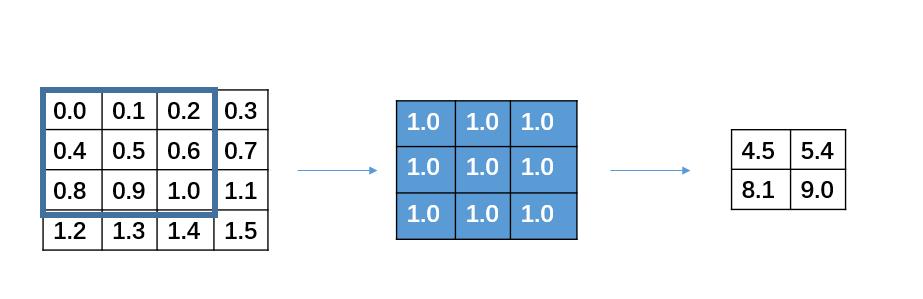 将卷积核与输入矩阵对应的位置进行乘加计算即可对于多维输入矩阵和多维卷积核的卷积计算将卷积后的结果进行堆叠作为最终卷积的输出结果。
将卷积核与输入矩阵对应的位置进行乘加计算即可对于多维输入矩阵和多维卷积核的卷积计算将卷积后的结果进行堆叠作为最终卷积的输出结果。
反卷积
tensorflow提供了tf.nn.conv2d_transpose函数来计算反卷积 功能说明计算反卷积(转置卷积)
- value4维的tensorfloat类型需要进行反卷积的矩阵
- filter卷积核参数格式[heightwidthoutput_channelsin_channels]这里需要注意output_channels和in_channels的顺序
- output_shape一维的Tensor设置反卷积输出矩阵的shape
- strides反卷积的步长
- padding"SAME"和"VALID"两种模式
- data_format和之前卷积参数一样
- name操作的名称
if __name__ "__main__":x1 tf.constant([4.5,5.4,8.1,9.0],shape[1,2,2,1],dtypetf.float32)dev_con1 tf.ones(shape[3,3,1,1],dtypetf.float32)y1 tf.nn.conv2d_transpose(x1,dev_con1,output_shape[1,4,4,1],strides[1,1,1,1],padding"VALID")sess tf.InteractiveSession()tf.global_variables_initializer()y1,x1 sess.run([y1,x1])print(y1)print(x1)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
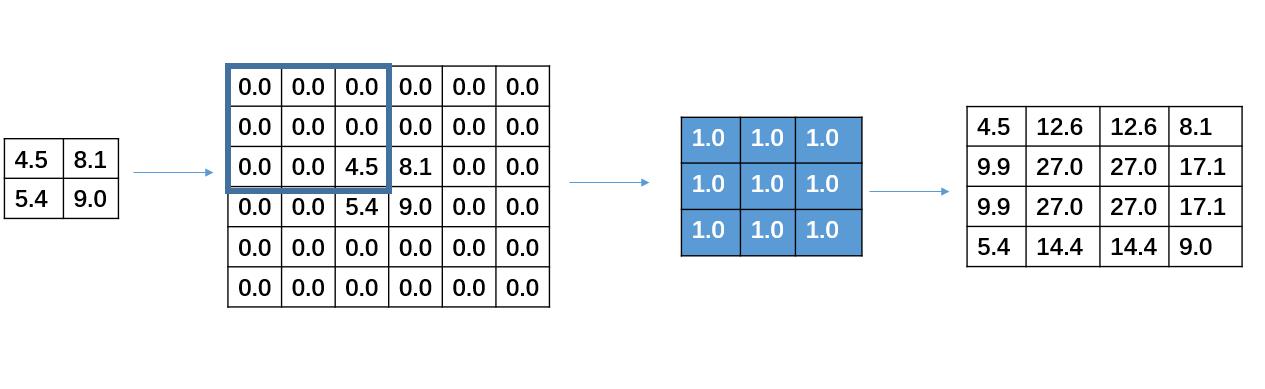 需要注意的是通过反卷积并不能还原卷积之前的矩阵只能从大小上进行还原反卷积的本质还是卷积只是在进行卷积之前会进行一个自动的padding补0从而使得输出的矩阵与指定输出矩阵的shape相同。框架本身会根据你设定的反卷积值来计算输入矩阵的尺寸如果shape不符合则会报错。 错误提示InvalidArgumentError (see above for traceback): Conv2DSlowBackpropInput这时候需要检查反卷积的参数与输入矩阵之间的shape是否符合。计算规则可以根据padding为SAME还是VALID来计算输入和输出矩阵的shape是否相符合。如上例中根据反卷积的参数来计算输入矩阵的shape因为padding是VALID模式所以我们套用ceil((i−k1)/s)ceil((4−31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2 ceil((i-k1)/s)ceil((4-31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2而输入矩阵x1的shape刚好是2*2所以符合。 上面介绍的反卷积的stride是1接下来看一个stride不为1的例子
需要注意的是通过反卷积并不能还原卷积之前的矩阵只能从大小上进行还原反卷积的本质还是卷积只是在进行卷积之前会进行一个自动的padding补0从而使得输出的矩阵与指定输出矩阵的shape相同。框架本身会根据你设定的反卷积值来计算输入矩阵的尺寸如果shape不符合则会报错。 错误提示InvalidArgumentError (see above for traceback): Conv2DSlowBackpropInput这时候需要检查反卷积的参数与输入矩阵之间的shape是否符合。计算规则可以根据padding为SAME还是VALID来计算输入和输出矩阵的shape是否相符合。如上例中根据反卷积的参数来计算输入矩阵的shape因为padding是VALID模式所以我们套用ceil((i−k1)/s)ceil((4−31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2 ceil((i-k1)/s)ceil((4-31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2ceil((i−k1)/s)ceil((4−31)/1)2而输入矩阵x1的shape刚好是2*2所以符合。 上面介绍的反卷积的stride是1接下来看一个stride不为1的例子
x1 tf.constant([4.5,5.4,8.1,9.0],shape[1,2,2,1],dtypetf.float32)dev_con1 tf.ones(shape[3,3,1,1],dtypetf.float32)y1 tf.nn.conv2d_transpose(x1,dev_con1,output_shape[1,6,6,1],strides[1,2,2,1],padding"VALID")sess tf.InteractiveSession()tf.global_variables_initializer()y1,x1 sess.run([y1,x1])
print(x1)print(y1)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
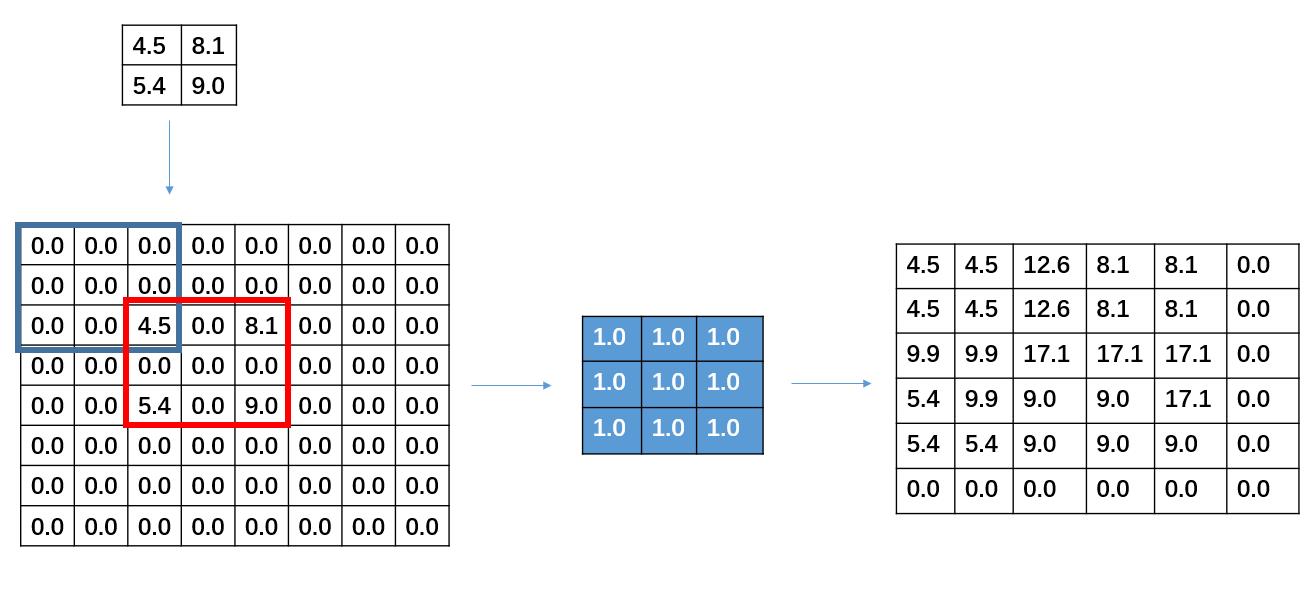 需要注意的是在进行反卷积的时候设置的stride并不是指反卷积在进行卷积时候卷积核的移动步长而是被卷积矩阵填充的padding仔细观察红色框内可以发现之前输入矩阵之间有一行和一列0的填充。
需要注意的是在进行反卷积的时候设置的stride并不是指反卷积在进行卷积时候卷积核的移动步长而是被卷积矩阵填充的padding仔细观察红色框内可以发现之前输入矩阵之间有一行和一列0的填充。
