前段时间看了一期《最强大脑》里面各种繁花曲线组合成了非常美丽的图形一时心血来潮想尝试自己用代码绘制繁花曲线想怎么组合就怎么组合。
真实的繁花曲线使用一种称为繁花曲线规的小玩意绘制繁花曲线规由相互契合大小两个圆组成用笔插在小圆上的一个孔中紧贴大圆的内壁滚动就可以绘制出漂亮的图案。这个过程可以做一个抽象有两个半径不相等的圆大圆位置固定小圆在大圆内部小圆紧贴着大圆内壁滚动求小圆上的某一点走过的轨迹。
进一步分析小圆的运动可以分解为两个部分小圆圆心绕大圆圆心公转、小圆绕自身圆心自转。设大圆圆心为A半径为Ra小圆圆心为B半径为Rb轨迹点为C半径为Rc(BC距离)设小圆公转的弧度为θ [0,∞)如图
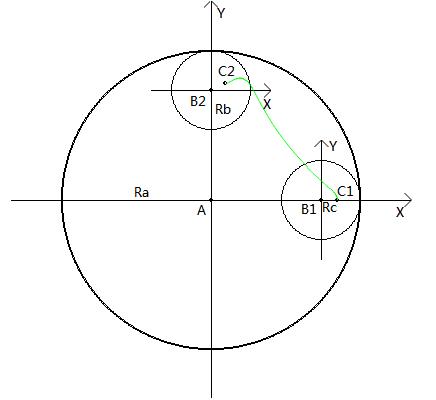
因为大圆的圆心坐标是固定的要求得小圆上的某点的轨迹需要先求出小圆当前时刻的圆心坐标再求出小圆自转的弧度最后求出小圆上某点的坐标。
第一步求小圆圆心坐标
小圆圆心的公转轨迹是一个半径为 RA- RB 的圆求小圆圆心坐标相当于是求半径为 RA- RB 的圆上θ 弧度对应的点的坐标。
圆上的点的坐标公式为
x r * cos(θ), y r * sin(θ)
小圆圆心坐标为( xa (Ra - Rb) * cos(θ), ya (Ra - Rb) * sin(θ) )
第二步求小圆自转弧度
设小圆自转弧度为α小圆紧贴大圆运动两者走过的路程相同因此有
Ra *θ Rb *α
小圆自转弧度α (Ra / Rb) *θ
第三步求点C坐标
点C相对小圆圆心B的公转轨迹是一个半径为 Rc 的圆类似第一步有
轨迹点C的坐标为( xa Rc* cos(θ), ya Rc* sin(θ))
按照以上算法分析用python代码实现如下
# -*- coding: utf-8 -*-
import math
功能
已知圆的圆心和半径获取某弧度对应的圆上点的坐标
入参
center圆心
radius半径
radian弧度
def get_point_in_circle(center, radius, radian):
return (center[0] radius * math.cos(radian), center[1] - radius * math.sin(radian))
功能
内外圆A和B内圆A沿着外圆B的内圈滚动已知外圆圆心、半径已知内圆半径已知公转弧度和绕点半径计算绕点坐标
入参
center_A外圆圆心
radius_A外圆半径
radius_B内圆半径
radius_C绕点半径
radian公转弧度
def get_point_in_child_circle(center_A, radius_A, radius_B, radius_C, radian):
# 计算内圆圆心坐标
center_B get_point_in_circle(center_A, radius_A - radius_B, radian)
# 计算绕点弧度(公转为逆时针则自转为顺时针)
radian_C 2.0*math.pi - ((radius_A / radius_B * radian) % (2.0*math.pi))
# 计算绕点坐标
return get_point_in_circle(center_B, radius_C, radian_C)
有两点需要注意
(1)屏幕坐标系左上角为原点垂直向下为Y正轴与数学坐标系Y轴方向相反所以第14行Y坐标为减法
(2)默认公转为逆时针则自转为顺时针所以第30行求自转弧度时使用了2π - α%(2π)
坐标已经计算出来接下来使用pygame绘制。思想是以0.01弧度为一个步长不断计算出新的坐标把一系列坐标连起来就会形成轨迹图。
为了能够形成一个封闭图形还需要知道绘制点什么时候会重新回到起点。想了一个办法以X轴正半轴为基准线每次绘制点到达基准线计算此时绘制点与起点的距离达到一定精度认为已经回到起点形成封闭图形。
计算两点距离(平方和)
def get_instance(p1, p2):
return (p1[0] - p2[0]) * (p1[0] - p2[0]) (p1[1] - p2[1]) * (p1[1] - p2[1])
功能
获取绕点路径的所有点的坐标
入参
center外圆圆心
radius_A外圆半径
radius_B内圆半径
radius_C绕点半径
shift_radian每次偏移的弧度默认0.01值越小精度越高计算量越大
def get_points(center, radius_A, radius_B, radius_C, shift_radian0.01):
# 转为实数
radius_A * 1.0
radius_B * 1.0
radius_C * 1.0
P2 2*math.pi # 一圈的弧度为 2PI
R_PER_ROUND int(P2/shift_radian/4) 1 # 一圈需要走多少步(弧度偏移多少次)
# 第一圈的起点坐标
start_point get_point_in_child_circle(center, radius_A, radius_B, radius_C, 0)
points [start_point]
# 第一圈的路径坐标
for r in range(1, R_PER_ROUND):
points.append(get_point_in_child_circle(center, radius_A, radius_B, radius_C, shift_radian*r))
# 以圈为单位每圈的起始弧度为 2PI*round某圈的起点坐标与第一圈的起点坐标距离在一定范围内认为路径结束
for round in range(1, 100):
s_radian round*P2
s_point get_point_in_child_circle(center, radius_A, radius_B, radius_C, s_radian)
if get_instance(s_point, start_point) <0.1:
break
points.append(s_point)
for r in range(1, R_PER_ROUND):
points.append(get_point_in_child_circle(center, radius_A, radius_B, radius_C, s_radian shift_radian*r))
return points
再加上绘制代码完整代码如下
# -*- coding: utf-8 -*-
import math
import random
功能
已知圆的圆心和半径获取某弧度对应的圆上点的坐标
入参
center圆心
radius半径
radian弧度
def get_point_in_circle(center, radius, radian):
return (center[0] radius * math.cos(radian), center[1] - radius * math.sin(radian))
功能
内外圆A和B内圆A沿着外圆B的内圈滚动已知外圆圆心、半径已知内圆半径、公转弧度已知绕点半径计算绕点坐标
入参
center_A外圆圆心
radius_A外圆半径
radius_B内圆半径
radius_C绕点半径
radian公转弧度
def get_point_in_child_circle(center_A, radius_A, radius_B, radius_C, radian):
# 计算内圆圆心坐标
center_B get_point_in_circle(center_A, radius_A - radius_B, radian)
# 计算绕点弧度(公转为逆时针则自转为顺时针)
radian_C 2.0*math.pi - ((radius_A / radius_B * radian) % (2.0*math.pi))
# 计算绕点坐标
center_C get_point_in_circle(center_B, radius_C, radian_C)
center_B_Int (int(center_B[0]), int(center_B[1]))
return center_B_Int, center_C
计算两点距离(平方和)
def get_instance(p1, p2):
return (p1[0] - p2[0]) * (p1[0] - p2[0]) (p1[1] - p2[1]) * (p1[1] - p2[1])
功能
获取绕点路径的所有点的坐标
入参
center外圆圆心
radius_A外圆半径
radius_B内圆半径
radius_C绕点半径
shift_radian每次偏移的弧度默认0.01值越小精度越高计算量越大
def get_points(center_A, radius_A, radius_B, radius_C, shift_radian0.01):
# 转为实数
radius_A * 1.0
radius_B * 1.0
radius_C * 1.0
P2 2*math.pi # 一圈的弧度为 2PI
R_PER_ROUND int(P2/shift_radian) 1 # 一圈需要走多少步(弧度偏移多少次)
# 第一圈的起点坐标
start_center, start_point get_point_in_child_circle(center_A, radius_A, radius_B, radius_C, 0)
points [start_point]
centers [start_center]
# 第一圈的路径坐标
for r in range(1, R_PER_ROUND):
center, point get_point_in_child_circle(center_A, radius_A, radius_B, radius_C, shift_radian*r)
points.append(point)
centers.append(center)
# 以圈为单位每圈的起始弧度为 2PI*round某圈的起点坐标与第一圈的起点坐标距离在一定范围内认为路径结束
for round in range(1, 100):
s_radian round*P2
s_center, s_point get_point_in_child_circle(center_A, radius_A, radius_B, radius_C, s_radian)
if get_instance(s_point, start_point) <0.1:
break
points.append(s_point)
centers.append(s_center)
for r in range(1, R_PER_ROUND):
center, point get_point_in_child_circle(center_A, radius_A, radius_B, radius_C, s_radian shift_radian*r)
points.append(point)
centers.append(center)
print(len(points)/R_PER_ROUND)
return centers, points
import pygame
from pygame.locals import *
pygame.init()
screen pygame.display.set_mode((600, 400))
clock pygame.time.Clock()
color_black (0, 0, 0)
color_white (255, 255, 255)
color_red (255, 0, 0)
color_yello (255, 255, 0)
center (300, 200)
radius_A 150
radius_B 110
radius_C 50
test_centers, test_points get_points(center, radius_A, radius_B, radius_C)
test_idx 2
draw_point_num_per_tti 5
while True:
for event in pygame.event.get():
if event.typepygame.QUIT:
pygame.quit()
exit(0)
screen.fill(color_white)
pygame.draw.circle(screen, color_black, center, int(radius_A), 2)
if test_idx < len(test_points):
pygame.draw.aalines(screen, (0, 0, 255), False, test_points[:test_idx], 1)
if test_idx pygame.draw.circle(screen, color_black, test_centers[test_idx], int(radius_B), 1) pygame.draw.aaline(screen, color_black, test_centers[test_idx], test_points[test_idx], 1) test_idx min(test_idx draw_point_num_per_tti, len(test_points)) clock.tick(50) pygame.display.flip() 效果
