杭电OJ_hdu3290_Themagicappletree

题目大意：给出一个有N(0

题目大意：给出一个有N(0

1.叶子节点生长出的苹果数量等于叶子节点的label。

2.某父亲节点有K个儿子节点，直到它的K个儿子节点都生长出苹果，父亲节点才开始生长苹果。父亲节点长出的苹果数量等于它的  所有儿子中苹果数量第(k+1)/2小的  儿子节点的苹果数量。

求根节点生长出的苹果数量。

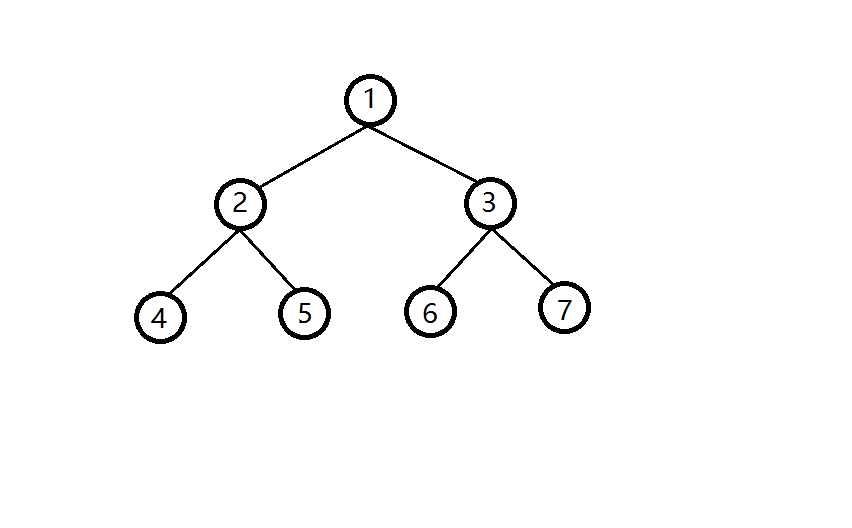
举个栗子：如下图所示，label为4,5,6,7的节点是叶节点，根据规则一，叶节点生长的苹果数量为他们的编号，那么他们生长出的苹果数量分别为4,5,6,7个。接下来，节点2,3的所有子节点有已经生长出苹果了，根据规则二，轮到节点2,3生长苹果了。节点2有2个子节点，根据计算：(2+1)/2 = 1，节点2的苹果数量等于它的所有儿子节点苹果数量中第1小的儿子节点苹果数量，也就是等于节点4的苹果数量。同样的，节点3的苹果数量为6。最后计算节点1的苹果数量即可。

1、用邻接表来存储这颗树。

2、用visit数组记录每个节点的入度，也就是方面后面找到根节点，根节点的入度为0。

3、根据题目规则，设计DFS搜索来求每个节点的苹果数量。

4、用优先队列来维护第(K+1)/2小的子节点苹果数量。

1 #include 2 #include 3 #include 4 #include 5 #include 6 #include 7 using namespace std; 8 9 const int N = 20010;10 11 /** 子节点结构 **/12 typedef struct LeafNode13 {14 int label; ///节点标号15 int next; ///下个子节点地址16 }LeafNode;17 18 /** 父节点结构 **/19 typedef struct Node20 {21 int label; ///节点标号22 int smaller; ///记录第几小的儿子23 int next; ///儿子节点地址24 }Node;25 26 Node tree[N]; ///邻接表存储苹果树27 int visit[N]; ///记录节点的入度28 LeafNode leaf[N];///静态数组存储叶节点29 int leafIndex; ///记录静态数组下一个可以分配的地址30 int n; ///节点数量31 32 /** dfs搜索root节点的苹果数量 **/33 int dfs( int root )34 {35 ///root节点为叶节点，直接返回苹果数量,即label36 if ( -1 == tree[root].next )37 return tree[root].label;38 39 ///root节点为父节点，计算该节点所有子节点的苹果数量，然后在返回40 int p = tree[root].next;41 priority_queue Q; ///用优先队列去维护第(k+1)/2小的子节点苹果数量42 43 while ( -1 != p )44 {45 Q.push( dfs( leaf[p].label ) );46 while ( int(Q.size()) > tree[root].smaller )///优先队列中元素的数量超过(k+1)/2，表示队首放的不是我们需要的结果47 Q.pop();48 p = leaf[p].next;49 }50 51 return Q.top();///优先队列队首放的就是结果52 }53 54 /** 初始化函数 **/55 void init(void)56 {57 leafIndex = 0;58 memset(visit, 0, sizeof(visit));59 }60 61 /** 把编号为label的子节点添加到编号为i的父节点的邻接表上 **/62 void addNode( int label, int i )63 {64 visit[label]++;65 int tmp = leafIndex++;66 leaf[tmp].label = label;67 leaf[tmp].next = tree[i].next;68 tree[i].next = tmp;69 }70 71 int main(void)72 {73 int i,j, label;74 while ( scanf("%d", 77 for (i = 1; i <= n; ++i)78 {79 scanf("%d", 80 tree[i].label = i; ///初始化节点i81 tree[i].smaller = (j+1)/2;82 tree[i].next = -1;83 while (j--) ///接受i节点的j个孩子84 {85 scanf("%d", 86 addNode(label, i);87 }88 }89 for ( i = 1; i <= n; ++i )90 {91 if ( 0 == visit[i] ) ///入度为0的节点为根节点，从根节点开始搜索92 {93 printf("%d\n",dfs(i));94 break;95 }96 }97 }98 return 0;99 }

杭电OJ_hdu3290_The magic apple tree