http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html
本文由LeftNotEasy发布于http://leftnoteasy.cnblogs.com, 本文可以被全部的转载或者部分使用但请注明出处如果有问题请联系wheeleastgmail.com
前言
第二篇的文章中谈到和部门老大一宁出去outing的时候他给了我相当多的机器学习的建议里面涉及到很多的算法的意义、学习方法等等。一宁上次给我提到如果学习分类算法最好从线性的入手线性分类器最简单的就是LDA它可以看做是简化版的SVM如果想理解SVM这种分类器那理解LDA就是很有必要的了。
谈到LDA就不得不谈谈PCAPCA是一个和LDA非常相关的算法从推导、求解、到算法最终的结果都有着相当的相似。
本次的内容主要是以推导数学公式为主都是从算法的物理意义出发然后一步一步最终推导到最终的式子LDA和PCA最终的表现都是解一个矩阵特征值的问题但是理解了如何推导才能更深刻的理解其中的含义。本次内容要求读者有一些基本的线性代数基础比如说特征值、特征向量的概念空间投影点乘等的一些基本知识等。除此之外的其他公式、我都尽量讲得更简单清楚。
LDA
LDA的全称是Linear Discriminant Analysis线性判别分析是一种supervised learning。有些资料上也称为是Fisher’s Linear Discriminant因为它被Ronald Fisher发明自1936年Discriminant这次词我个人的理解是一个模型不需要去通过概率的方法来训练、预测数据比如说各种贝叶斯方法就需要获取数据的先验、后验概率等等。LDA是在目前机器学习、数据挖掘领域经典且热门的一个算法据我所知百度的商务搜索部里面就用了不少这方面的算法。
LDA的原理是将带上标签的数据点通过投影的方法投影到维度更低的空间中使得投影后的点会形成按类别区分一簇一簇的情况相同类别的点将会在投影后的空间中更接近。要说明白LDA首先得弄明白线性分类器(Linear Classifier)因为LDA是一种线性分类器。对于K-分类的一个分类问题会有K个线性函数
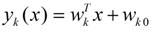
当满足条件对于所有的j都有Yk > Yj,的时候我们就说x属于类别k。对于每一个分类都有一个公式去算一个分值在所有的公式得到的分值中找一个最大的就是所属的分类了。
上式实际上就是一种投影是将一个高维的点投影到一条高维的直线上LDA最求的目标是给出一个标注了类别的数据集投影到了一条直线之后能够使得点尽量的按类别区分开当k2即二分类问题的时候如下图所示
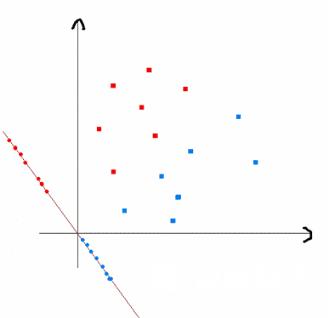
红色的方形的点为0类的原始点、蓝色的方形点为1类的原始点经过原点的那条线就是投影的直线从图上可以清楚的看到红色的点和蓝色的点被原点明显的分开了这个数据只是随便画的如果在高维的情况下看起来会更好一点。下面我来推导一下二分类LDA问题的公式
假设用来区分二分类的直线投影函数)为
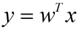
LDA分类的一个目标是使得不同类别之间的距离越远越好同一类别之中的距离越近越好所以我们需要定义几个关键的值。
类别i的原始中心点为Di表示属于类别i的点)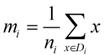
类别i投影后的中心点为
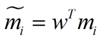
衡量类别i投影后类别点之间的分散程度方差为
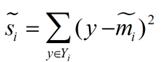
最终我们可以得到一个下面的公式表示LDA投影到w后的损失函数

我们分类的目标是使得类别内的点距离越近越好集中类别间的点越远越好。分母表示每一个类别内的方差之和方差越大表示一个类别内的点越分散分子为两个类别各自的中心点的距离的平方我们最大化J(w)就可以求出最优的w了。想要求出最优的w可以使用拉格朗日乘子法但是现在我们得到的J(w)里面w是不能被单独提出来的我们就得想办法将w单独提出来。
我们定义一个投影前的各类别分散程度的矩阵这个矩阵看起来有一点麻烦其实意思是如果某一个分类的输入点集Di里面的点距离这个分类的中心店mi越近则Si里面元素的值就越小如果分类的点都紧紧地围绕着mi则Si里面的元素值越更接近0.
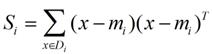
带入Si将J(w)分母化为
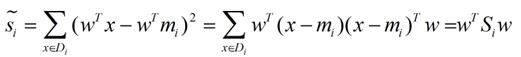
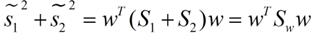
同样的将J(w)分子化为
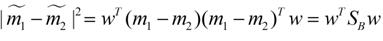
这样损失函数可以化成下面的形式
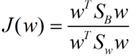
这样就可以用最喜欢的拉格朗日乘子法了但是还有一个问题如果分子、分母是都可以取任意值的那就会使得有无穷解我们将分母限制为长度为1这是用拉格朗日乘子法一个很重要的技巧在下面将说的PCA里面也会用到如果忘记了请复习一下高数并作为拉格朗日乘子法的限制条件带入得到
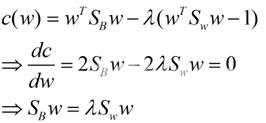
这样的式子就是一个求特征值的问题了。
对于N(N>2)分类的问题我就直接写出下面的结论了
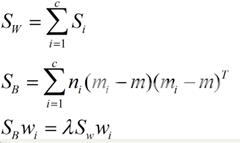
这同样是一个求特征值的问题我们求出的第i大的特征向量就是对应的Wi了。
这里想多谈谈特征值特征值在纯数学、量子力学、固体力学、计算机等等领域都有广泛的应用特征值表示的是矩阵的性质当我们取到矩阵的前N个最大的特征值的时候我们可以说提取到的矩阵主要的成分这个和之后的PCA相关但是不是完全一样的概念。在机器学习领域不少的地方都要用到特征值的计算比如说图像识别、pagerank、LDA、还有之后将会提到的PCA等等。
下图是图像识别中广泛用到的特征脸eigen face提取出特征脸有两个目的首先是为了压缩数据对于一张图片只需要保存其最重要的部分就是了然后是为了使得程序更容易处理在提取主要特征的时候很多的噪声都被过滤掉了。跟下面将谈到的PCA的作用非常相关。

特征值的求法有很多求一个D * D的矩阵的时间复杂度是O(D^3), 也有一些求Top M的方法比如说power method它的时间复杂度是O(D^2 * M), 总体来说求特征值是一个很费时间的操作如果是单机环境下是很局限的。
PCA
主成分分析PCA与LDA有着非常近似的意思LDA的输入数据是带标签的而PCA的输入数据是不带标签的所以PCA是一种unsupervised learning。LDA通常来说是作为一个独立的算法存在给定了训练数据后将会得到一系列的判别函数discriminate function之后对于新的输入就可以进行预测了。而PCA更像是一个预处理的方法它可以将原本的数据降低维度而使得降低了维度的数据之间的方差最大也可以说投影误差最小具体在之后的推导里面会谈到。
方差这个东西是个很有趣的有些时候我们会考虑减少方差比如说训练模型的时候我们会考虑到方差-偏差的均衡有的时候我们会尽量的增大方差。方差就像是一种信仰强哥的话不一定会有很严密的证明从实践来说通过尽量增大投影方差的PCA算法确实可以提高我们的算法质量。
说了这么多推推公式可以帮助我们理解。我下面将用两种思路来推导出一个同样的表达式。首先是最大化投影后的方差其次是最小化投影后的损失投影产生的损失最小。
最大化方差法
假设我们还是将一个空间中的点投影到一个向量中去。首先给出原空间的中心点
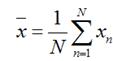 假设u1为投影向量投影之后的方差为
假设u1为投影向量投影之后的方差为
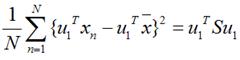 上面这个式子如果看懂了之前推导LDA的过程应该比较容易理解如果线性代数里面的内容忘记了可以再温习一下优化上式等号右边的内容还是用拉格朗日乘子法
上面这个式子如果看懂了之前推导LDA的过程应该比较容易理解如果线性代数里面的内容忘记了可以再温习一下优化上式等号右边的内容还是用拉格朗日乘子法
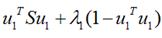 将上式求导使之为0得到
将上式求导使之为0得到
最小化损失法 假设输入数据x是在D维空间中的点那么我们可以用D个正交的D维向量去完全的表示这个空间这个空间中所有的向量都可以用这D个向量的线性组合得到。在D维空间中有无穷多种可能找这D个正交的D维向量哪个组合是最合适的呢 假设我们已经找到了这D个向量可以得到 下图是PCA的投影的一个表示黑色的点是原始的点带箭头的虚线是投影的向量Pc1表示特征值最大的特征向量pc2表示特征值次大的特征向量两者是彼此正交的因为这原本是一个2维的空间所以最多有两个投影的向量如果空间维度更高则投影的向量会更多。 总结 本次主要讲了两种方法PCA与LDA两者的思想和计算方法非常类似但是一个是作为独立的算法存在另一个更多的用于数据的预处理的工作。另外对于PCA和LDA还有核方法本次的篇幅比较大了先不说了以后有时间再谈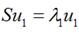 这是一个标准的特征值表达式了λ对应的特征值u对应的特征向量。上式的左边取得最大值的条件就是λ1最大也就是取得最大的特征值的时候。假设我们是要将一个D维的数据空间投影到M维的数据空间中M
这是一个标准的特征值表达式了λ对应的特征值u对应的特征向量。上式的左边取得最大值的条件就是λ1最大也就是取得最大的特征值的时候。假设我们是要将一个D维的数据空间投影到M维的数据空间中M 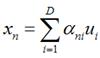 我们可以用近似法来表示投影后的点
我们可以用近似法来表示投影后的点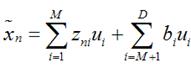 上式表示得到的新的x是由前M 个基的线性组合加上后D - M个基的线性组合注意这里的z是对于每个x都不同的而b对于每个x是相同的这样我们就可以用M个数来表示空间中的一个点也就是使得数据降维了。但是这样降维后的数据必然会产生一些扭曲我们用J描述这种扭曲我们的目标是使得J最小
上式表示得到的新的x是由前M 个基的线性组合加上后D - M个基的线性组合注意这里的z是对于每个x都不同的而b对于每个x是相同的这样我们就可以用M个数来表示空间中的一个点也就是使得数据降维了。但是这样降维后的数据必然会产生一些扭曲我们用J描述这种扭曲我们的目标是使得J最小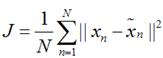 上式的意思很直观就是对于每一个点将降维后的点与原始的点之间的距离的平方和加起来求平均值我们就要使得这个平均值最小。我们令
上式的意思很直观就是对于每一个点将降维后的点与原始的点之间的距离的平方和加起来求平均值我们就要使得这个平均值最小。我们令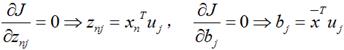 将上面得到的z与b带入降维的表达式
将上面得到的z与b带入降维的表达式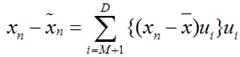 将上式带入J的表达式得到
将上式带入J的表达式得到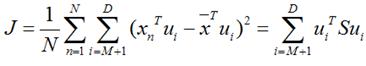 再用上拉普拉斯乘子法此处略可以得到取得我们想要的投影基的表达式为
再用上拉普拉斯乘子法此处略可以得到取得我们想要的投影基的表达式为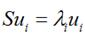 这里又是一个特征值的表达式我们想要的前M个向量其实就是这里最大的M个特征值所对应的特征向量。证明这个还可以看看我们J可以化为
这里又是一个特征值的表达式我们想要的前M个向量其实就是这里最大的M个特征值所对应的特征向量。证明这个还可以看看我们J可以化为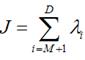 也就是当误差J是由最小的D - M个特征值组成的时候J取得最小值。跟上面的意思相同。
也就是当误差J是由最小的D - M个特征值组成的时候J取得最小值。跟上面的意思相同。
