本节中的第一种高级排序算法是归并排序。“归并”一词,意为“合并”。顾名思义,归并排序算法就是一个先把数列拆分为子数列,对子数列进行排序后,再把有序的子数列合并为完整的有序数列的算法。它实际上采用了分治的思想。
归并排序的平均时间复杂度是O(nlgn),最好情况下的时间复杂度是O(nlgn),最坏情况下的时间复杂度也是O(nlgn)。它的空间复杂度是O(1)。另外,归并排序还是一个稳定的排序算法。
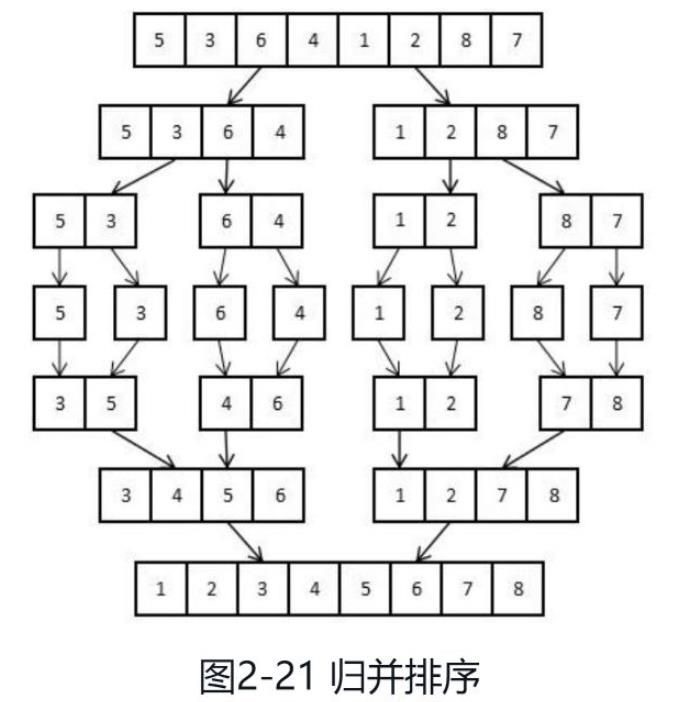
以升序排序为例,归并算法的流程如图2-21所示。
原始数组是一个有8个数的无序数组。一次操作后,把8个数的数组分成两个4个数组成的无序数组。每个操作都将无序数组分成两半,直至所有最小的子数组仅包含一个元素。当数组里只有一个元素时,这个数组必定是有序的。然后,程序开始把小的有序数组每两个合并成为大的有序数组。首先是将两个包含一个数的数组合并成一个包含两个数的数组,然后再把两个包含两个数的数组合并成一个包含四个数的数组,最后合并成一个包含八个数的数组。当所有有序数组合并完毕时,形成的最长有序数组就完成排序。
归并排序代码:
#归并排序
nums = [5,3,6,4,1,2,8,7]
def MergeSort(num):
if(len(num)<=1): #递归边界条件
return num #到达边界时返回当前的子数组
mid = int(len(num)/2) #求出数组的中位数
llist,rlist = MergeSort(num[:mid]),MergeSort(num[mid:])#调用函数分别为左右数组排序
result = []
i,j = 0,0
while i < len(llist) and j < len(rlist): #while循环用于合并两个有序数组
if rlist[j]<llist[i]:
result.append(rlist[j])
j += 1
else:
result.append(llist[i])
i += 1
result += llist[i:]+rlist[j:] #把数组未添加的部分加到结果数组末尾
return result #返回已排序的数组
print(MergeSort(nums))运行程序,输出结果为:
[1,2,3,4,5,6,7,8]
在MergeSort()函数中,首先进行的是边界条件判断。当一个只包含一个元素的数组作为函数参数时,该元素单独存在于数组中,因此该数组已经达到了最小大小。完成递归分解数组的任务后,只需将分解后的数组返回到上一层递归即可。
如果未排序数组的长度仍然大于1,那么使用变量mid来存储数组最中间的下标,把未排序数组分成左右两个子数组。然后,新建两个数组,用于存储排好序的左右子数组。这里使用了递归的思想。我们只把MergeSort()函数视为一个为列表排序的函数,尽管在MergeSort()函数内部,也可以调用函数本身对两个子数组进行排序。
随后,使用while循环合并两个已经有序的数组。由于不能确定两个数组中元素的相对大小,所以我们采用i和j两个变量分别标记在左子数组和右子数组中等待加入的元素的位置。当while循环结束时,可能一个子数组的末尾还剩余一些最大的元素没有被添加到result列表中,所以result+=llist[i:]+rlist[j:]语句是为了防止漏掉这些元素。数组合并完成后,函数输出有序数组。
