python绘制二维直方图的代码实现

• hist+scatter
• hist2d

如果想描述二维数据的分布特征，那么一个直方图显然是不够用的，为此可使用两个直方图分别代表x和y方向上的分布情况，同时透过散点图查看其整体的分布特征。

下面创建一组二元高斯分布的数据，用于直方图测试。多元高斯分布的主要参数仍为期望和方差，但所谓多元分布，在坐标层面的表现就是坐标轴的个数，也就是向量维度。所以N个元素对应N维向量，也就有N个期望；而方差则进化为了协方差矩阵

import numpy as np
import matplotlib.pyplot as plt
mean = [0, 0]
cov = [[0, 1], [10, 0]]
x, y = np.random.multivariate_normal(mean, cov, 5000).T

其中，x,y就是待统计的数据。

fig = plt.figure()
gs = fig.add_gridspec(2, 2,  
    width_ratios=(4, 1),  
    height_ratios=(1, 4))
ax = fig.add_subplot(gs[1, 0])
ax.scatter(x, y, marker='x')        # 散点图绘制
xHist = fig.add_subplot(gs[0, 0], sharex=ax)
xHist.tick_params(axis="x", labelbottom=False)
yHist = fig.add_subplot(gs[1, 1], sharey=ax)
yHist.tick_params(axis="y", labelleft=False)
binwidth = 0.25
lim = (int(np.max(np.abs([x,y]))/0.25) + 1) * 0.25
bins = np.arange(-lim, lim + binwidth, binwidth)
xHist.hist(x, bins=bins)
yHist.hist(y, bins=bins, orientation='horizontal')
plt.show()

其中，tick_params用于取消直方图左侧和下面的坐标刻度，效果如下

相比之下，hist2d可以更加便捷地绘制直方图，并以图像的形式反馈回来

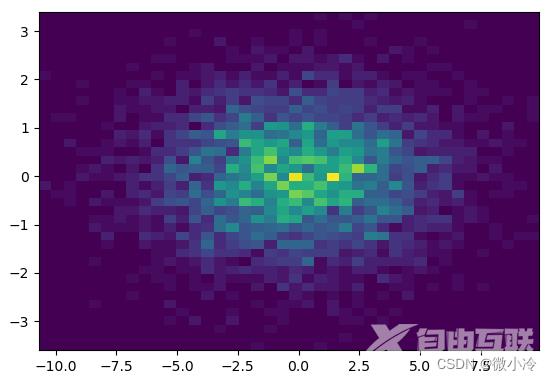
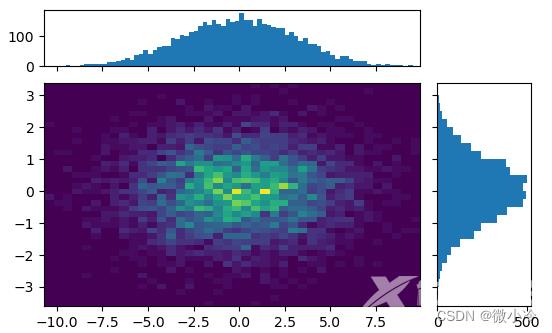
当然，也可以把hist+scatter图中的散点图代之以hist2d

fig = plt.figure()
gs = fig.add_gridspec(2, 2,  
    width_ratios=(4, 1),  
    height_ratios=(1, 4))
ax = fig.add_subplot(gs[1, 0])
ax.hist2d(x, y, bins=40)        # 散点图绘制
xHist = fig.add_subplot(gs[0, 0], sharex=ax)
xHist.tick_params(axis="x", labelbottom=False)
yHist = fig.add_subplot(gs[1, 1], sharey=ax)
yHist.tick_params(axis="y", labelleft=False)
binwidth = 0.25
lim = (int(np.max(np.abs([x,y]))/0.25) + 1) * 0.25
bins = np.arange(-lim, lim + binwidth, binwidth)
xHist.hist(x, bins=bins)
yHist.hist(y, bins=bins, orientation='horizontal')
plt.show()

到此这篇关于python绘制二维直方图的代码实现的文章就介绍到这了,更多相关python绘制二维直方图内容请搜索自由互联以前的文章或继续浏览下面的相关文章希望大家以后多多支持自由互联！