一、选择题
1.1、如下代码输出的是什么( )
char a=101;
int sum=200;
a+=27;sum+=a;
printf("%d\n",sum);A: 327 B: 99 C: 328 D: 72
题解:这题考察对常见数据结构存储的理解,容易出错在a+=27这个地方,char类型的数据存储范围为-128--127,当a+27之后会超过数据存储范围,a就变为-128,sum加等上-128后就变成了72,所以这题选D。
1.2、对于下面代码执行后输出的是什么( )
int value = 1024;
char condition = *((char*)(&value));
if(condition) value += 1; condition = *((char*)(&value));
if(condition) value += 1; condition = *((char*)(&value));
printf("%d %d", value, condition);A: 1026 1 B: 1025 0 C: 1025 1 D: 1024 0
题解:这个也是考察数据的存储的知识,重点考察了数据类型转化中可能出现的整型提升和截断。当低精度整型数据类型向高精度整型数据类型转化时会发生整型提升, 与此相反的是发生整型截断,本题&value为int*类型数据,被强制转化为char*类型数据,由高精度转化为低精度,发生整型截断,int变量value的值为1024,其二进制表示为00000000 00000000 00000100 00000000。经过强制类型转换后,通过*((char*)(&value))获取的字符值将是最低有效字节,即第一个字节00000000所代表的十进制数值为0。
所有赋值之后condition为0,所有的判断语句都不执行,value为1024,condition为0,选D。
1.3、假设在32位机器上,读代码选结果( )
void func(char para[100])
{void *p = malloc(100);printf("%d, %d\n", sizeof(para), sizeof(p));
}A: 4,4 B: 100,4 C: 4,100 D: 100,100
题解:本体涉及到计算机32位和64位中指针的字节区别,然后就是数组在传递参数过程后,对数组的理解。在32位的机器上,指针占4个字节,在63位机器中,指针占8个字节。sizeof(p)是求p指针的大小,所以是4;对于sizeof(para),尽管para在函数声明中写作char para[100],但在函数内部,para已经被转换为指向char类型的指针。指针的大小是4字节,因此sizeof(para)也得到了4。选A。
1.4、以下程序执行后的输出结果为( )
#include <stdio.h>
void func(char* p) { p = p + 1; }
int main()
{
char s[] = { '1', '2', '3', '4' };
func(s);
printf("%c", *s);
return 0;
}A:2
B:编译错误
C:1
D:无法确定
题解:本题涉及到函数栈帧创建和销毁的理解,对func函数传递一个schar类型数组,用p接收数组的首地址,然后p指针往后跳一个字节,当这个函数执行完后,函数中的指针p也随之销毁,而且void没有返回值。最后输出s,解引用首地址,得到首地址的值为1。选C。
1.5、已知数组D的定义是int D[4][8]; 现在需要把这个数组作为实参传递给一个函数进行处理。下列可以作为对应的形参变量说明的是【多选】( )
A:int D[4][]
B:int *s[8]
C:int(*s)[8]
D: int D[][8]
题解:
- 选项 A: int D[4][] 是不正确的,因为在形参中,数组的第一个维度必须给定大小。
- 选项 B: int *s[8] 是一个包含 8 个指向 int 类型的指针的数组,它并不符合传递二维数组的要求。
- 选项 C: int(*s)[8] 是一个指向包含 8 个 int 类型元素的数组的指针。这种方式可以正确地接受二维数组D[4][8]作为实参。
- 选项 D: int D[][8] 是另一种表示二维数组的方式,其中省略了第一个维度的大小,保留了第二个维度的大小。这种方式也可以正确地接受二维数组D[4][8]作为实参。
因此,选项 C 和选项 D 都可以作为对应的形参变量说明来接受数组D[4][8]作为实参。
二、编程题
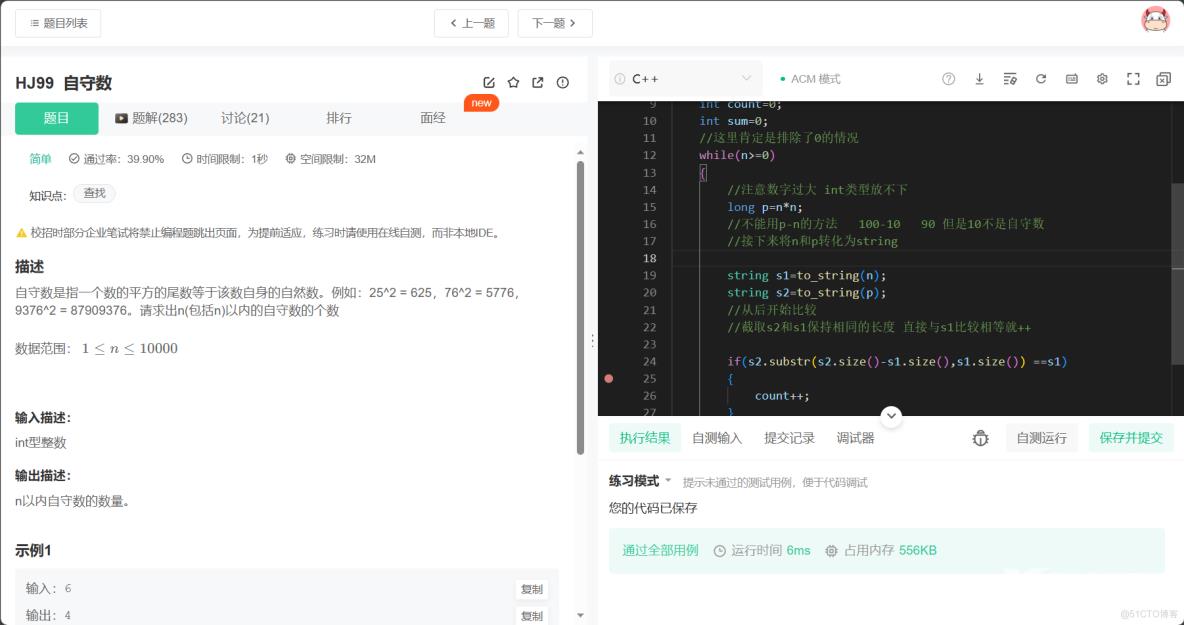
2.1、HJ99 自守数
题目描述:
自守数是指一个数的平方的尾数等于该数自身的自然数。例如:25^2 = 625,76^2 = 5776,9376^2 = 87909376。请求出n(包括n)以内的自守数的个数
数据范围:
输入描述:
int型整数
输出描述:
n以内自守数的数量。

题解思路:
这个题目是要求自守数的个数,所以设置一个count来记录符合的个数。其次就是在平方的时候要注意int类型的数据限制,要用long类型来存。再者就是我原本用的是n*n-n来确定最后一个是否为0来决定是不是自守数,跑出来发现这种写法漏了很多,比如n=10,n*n=100,90最后一个确实是0,但是10不是自守数,最后我实现的方法是将n*n和n全部转化为string类型数据,再将s2中从第s2.size()-s1.size()位置后s1.size()长度,与s1进行比较,相等count++。最后输出结果
实现代码:
#include <iostream>
#include<string>
using namespace std;
int main() {
int n;
cin>>n;
//0肯定是自守数
int count=0;
int sum=0;
//这里肯定是排除了0的情况
while(n>=0)
{
//注意数字过大 int类型放不下
long p=n*n;
//不能用p-n的方法 100-10 90 但是10不是自守数
//接下来将n和p转化为string
string s1=to_string(n);
string s2=to_string(p);
//从后开始比较
//截取s2和s1保持相同的长度 直接与s1比较相等就++
if(s2.substr(s2.size()-s1.size(),s1.size()) ==s1)
{
count++;
}
n--;
}
cout<<count<<endl;
}
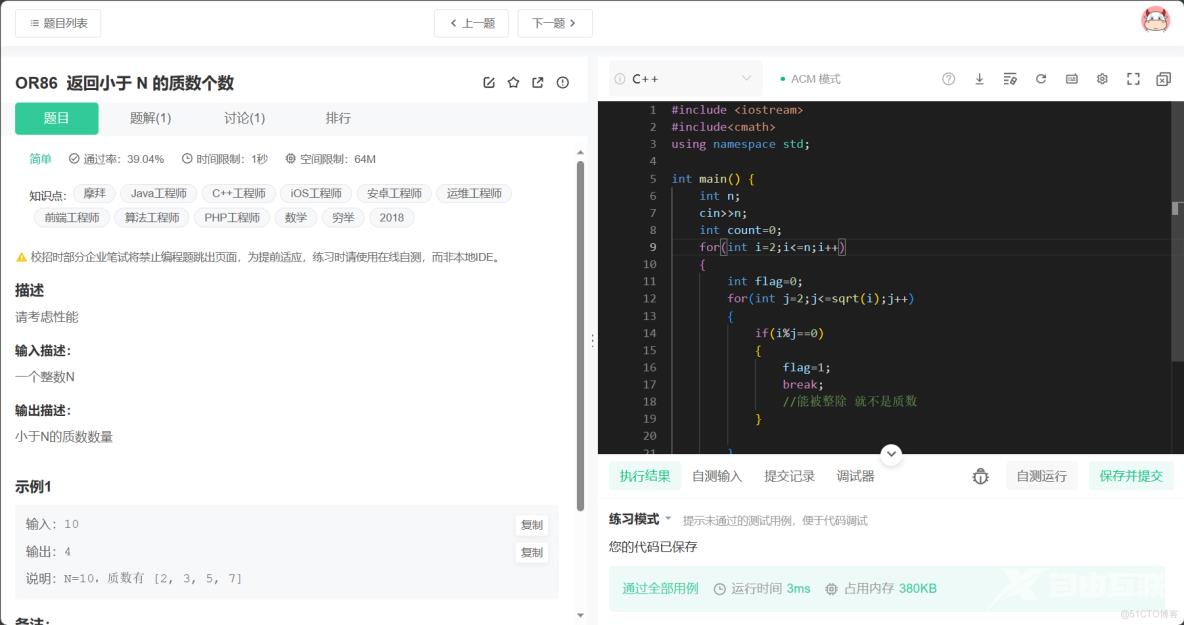
2.2、返回小于 N 的质数个数
描述
请考虑性能
输入描述:
一个整数N
输出描述:
小于N的质数数量
题解思路:
本题难点在注意性能,在输入输出的时候scanf和printf都要比cin和cout快,其次是在取余判断是否为质数时,我们用的放大的思想去找因子,因为7一个数的因子不可能超过其平方根,如果有一个因子超过其平方根,那么相反的就是另外一个因子小于其平方根。这里可以简化循环判断时间,减少不必要的判断提高性能。
实现代码:
#include <iostream>
#include<cmath>
using namespace std;
int main() {
int n;
cin>>n;
int count=0;
for(int i=2;i<=n;i++)
{
int flag=0;
for(int j=2;j<=sqrt(i);j++)
{
if(i%j==0)
{
flag=1;
break;
//能被整除 就不是质数
}
}
if(flag==0)
{
count++;
}
}
cout<<count<<endl;
}