二叉树
110. 平衡二叉树
题意:给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例:
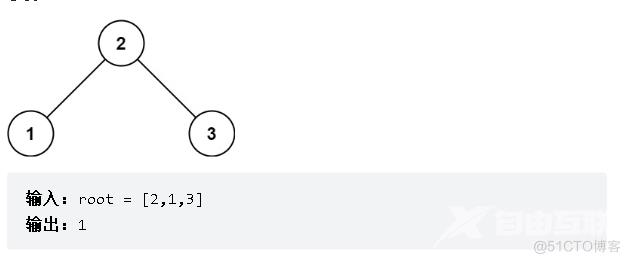
思路:本题我们可以自下而上判断二叉树是否为平衡二叉树,以上图为示例,我们先判断15是不是平衡二叉树,很明显是的,此时就引出了我们递归的终止条件,当root为空时,此时返回0;再判断20节点,发现高度差为0,符合条件,此时的高度变为1+子二叉树的最大高度,此时为2,以此往上判断;而当高度差大于-1时,这时我们就会有新的判断条件,只要有一个子树为-1,那么之后的所有子树都为-1,这样我们在返回主函数判断时,判断的依据也自然就是返回的值是否等于-1
递归代码:
int BalanceAVL(TreeNode *root)
{
if(nullptr==root)//递归终止条件
{
return 0;
}
int leftheigh=BalanceAVL(root->left);//左子树高度
if(leftheigh==-1)
{
return -1;
}
int rightheigh=BalanceAVL(root->right);//右子树高度
if(rightheigh==-1)
{
return -1;
}
int heighdeffer;//节点最大高度
if(leftheigh-rightheigh>1||leftheigh-rightheigh<-1)
{
heighdeffer=-1;
}
else
{
heighdeffer=1+max(leftheigh,rightheigh);
}
return heighdeffer;
}
bool isBalanced(TreeNode* root) {
return BalanceAVL(root)!=-1?true:false;
}513. 找树左下角的值
题意:给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。假设二叉树中至少有一个节点。
示例:
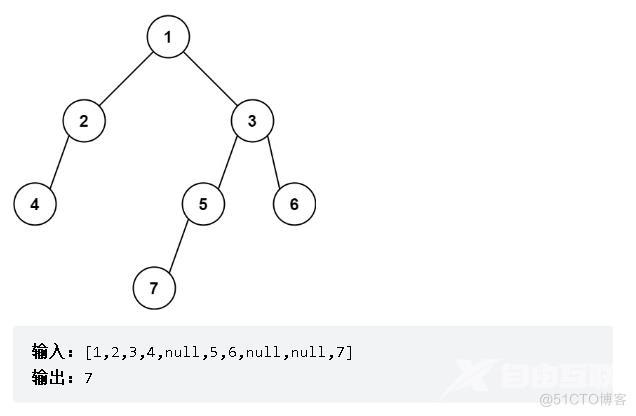
思路:本题我们需要确定一个最大深度,因为题目给出的最左下角的值是按深度确定的,准确的是最大深度的最左侧值,因此,上图中的最左下角的值是7,而并非4。所有我们需要遍历每个叶子节点,并且递归终止条件中给出另一个条件去交换最左侧节点的值
递归代码:
int maxheigh=INT_MIN;//最大深度
int leftVal;
void maxLiftVal(TreeNode* root,int tmpheigh)
{
if(nullptr==root->left&&nullptr==root->right)
{
if(maxheigh<tmpheigh)
{
maxheigh=tmpheigh;
leftVal=root->val;
}
return;
}
if(root->left)
{
maxLiftVal(root->left,tmpheigh+1);
}
if(root->right)
{
maxLiftVal(root->right,tmpheigh+1);
}
}
int findBottomLeftValue(TreeNode* root) {
maxLiftVal(root,1);
return leftVal;
}112. 路径总和
题意:给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。叶子节点 是指没有子节点的节点。
示例:
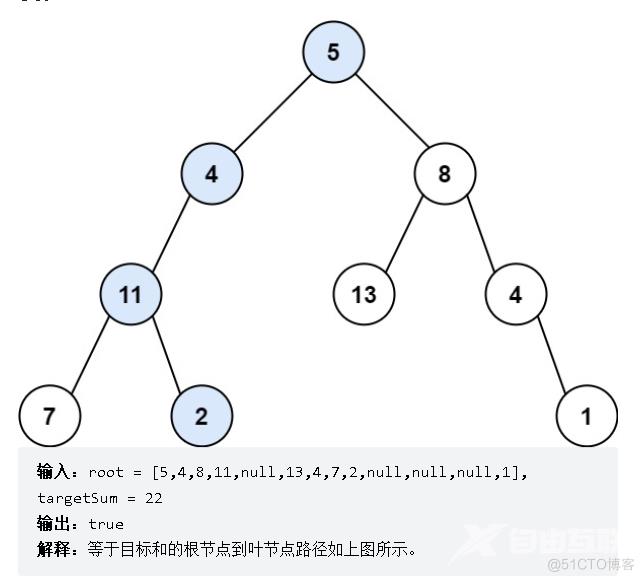
思路:本题的思路就是使用递归模拟回溯,减去目标值targetsum,当节点走到叶子节点且targetsum为0时,说明该二叉树有符合条件的路径。
首先,要将目标值统一减去根节点的值,因为每个路径都会包括根节点;其次,我们需要模拟目标值减少的操作,当走到叶子节点发现目标值不为0时,就需要将目标值加回来,然后从另一条路径再次判断。这里我也陷入了一种循环,就是我们在减完目标值后,确实需要立刻判断目标值和所处位置是否满足条件,但是我认为直接在函数中递归判断就行,但是,实际测试发现,还是需要使用if语句作为条件判断依据;这里相当于if语句判断完,整个函数就可以推出了,而继续递归判断的话,只能说明该路径满足,而递归不会停止,所以,此时代码的判断条件就变为了二叉树中,最右边路径之和是否等于目标值。
递归代码:
bool pathRBTree(TreeNode* root,int targetSum)
{
if(nullptr==root->left&&nullptr==root->right)//走到根节点开始判断,是否满足条件
{
if(targetSum==0)
{
return true;
}
return false;
}
if(root->left)
{
targetSum-=root->left->val;//这里模拟的是回溯算法
if(pathRBTree(root->left,targetSum))//减完目标值就需要直接判断是否满足条件
{
return true;
}
targetSum+=root->left->val;
}
if(root->right)
{
targetSum-=root->right->val;
if(pathRBTree(root->right,targetSum))
{
return true;
}
targetSum+=root->right->val;
}
return false;
}
bool hasPathSum(TreeNode* root, int targetSum) {
if(nullptr==root)//根节点为空,直接判断错误
{
return false;
}
return pathRBTree(root,targetSum-(root->val));//统一不计算根节点
}106. 从中序与后序遍历序列构造二叉树
题意:给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例:

思路:本题思路非常简单,就是利用后序遍历的特点,每个后序遍历数组的最后一个元素就是一棵树的根节点,然后再将中序遍历不断分割,这样一直递归下去,即可得到二叉树本来的样子
递归代码:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if(postorder.size()==0)//以后序遍历数组为目标,因为每次递归都会移除一个元素
{
return nullptr;
}
int rootval=postorder[postorder.size()-1];//锁定后序遍历最后一个元素,这就是根节点
TreeNode* root=new TreeNode(rootval);
int mid;//找到中序遍历的分割位置
for(mid=0;mid<inorder.size();mid++)
{
if(inorder[mid]==rootval)
{
break;
}
}
postorder.resize(postorder.size()-1);
vector<int> leftinorder(inorder.begin(),inorder.begin()+mid);//分割中序遍历
vector<int> rightinorder(inorder.begin()+mid+1,inorder.end());
vector<int> leftpostorder(postorder.begin(),postorder.begin()+leftinorder.size());//分割后序遍历
vector<int> rightpostorder(postorder.begin()+leftinorder.size(),postorder.end());
root->left=buildTree(leftinorder,leftpostorder);
root->right=buildTree(rightinorder,rightpostorder);
return root;
}