算法练习-day14

二叉树

110. 平衡二叉树

题意：给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例：

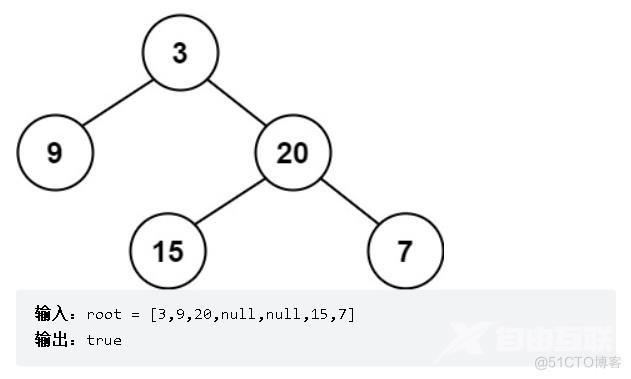
       思路：本题我们可以自下而上判断二叉树是否为平衡二叉树，以上图为示例，我们先判断15是不是平衡二叉树，很明显是的，此时就引出了我们递归的终止条件，当root为空时，此时返回0；再判断20节点，发现高度差为0，符合条件，此时的高度变为1+子二叉树的最大高度，此时为2，以此往上判断；而当高度差大于-1时，这时我们就会有新的判断条件，只要有一个子树为-1，那么之后的所有子树都为-1，这样我们在返回主函数判断时，判断的依据也自然就是返回的值是否等于-1

C++代码：

int intDepth(TreeNode* root)
    {
        if(nullptr==root)//当为空节点时，返回0(即叶子节点之后的节点没有高度)
        {
            return 0;
        }
        int leftHeigh=intDepth(root->left);
        if(leftHeigh==-1)//当有一个节点高度为-1时，就说明该二叉树已经不是平衡二叉树了，所以之后的节点都会继承-1，最后返回给根节点
        {
            return -1;
        }
        int rightHeigh=intDepth(root->right);
        if(rightHeigh==-1)
        {
            return -1;
        }
        int result=rightHeigh-leftHeigh;
        if(result<-1||result>1)//当两高度已经不满足条件时，直接返回-1
        {
            result =-1;
        }
        else//两高度差还满足条件，此时根节点高度为1+最大高度
        {
            result=max(leftHeigh,rightHeigh)+1;
        }
        return result;
    }
    bool isBalanced(TreeNode* root) {
        return intDepth(root)==-1?false:true;
    }

257. 二叉树的所有路径

题意：给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。叶子节点 是指没有子节点的节点。

示例：

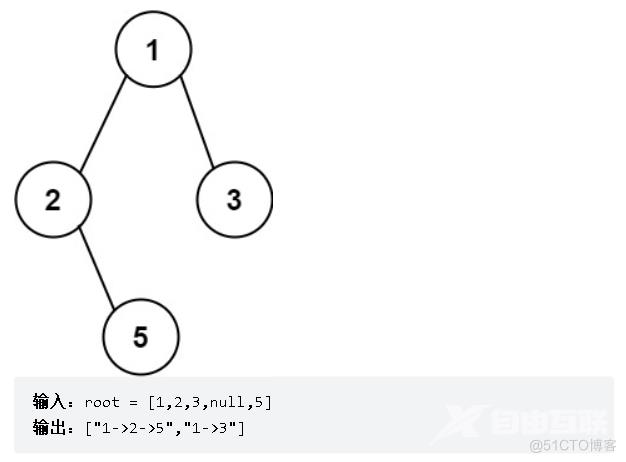
       思路：本题的思路就是使用前序遍历和回溯的方法，先将我们看到的节点加入到给定的数组中，用于记录路径的节点，然后再通过返回条件，让数组中元素以->的方式加入arr中，最后在返回到上一步，找是否有不同路径需要保存

C++代码：

vector<string> arr;
    void Allpath(TreeNode* root,vector<int>& tmp)
    {
        tmp.push_back(root->val);//前序遍历写法
        if(nullptr==root->left&&nullptr==root->right)//走到一个路径的末尾了
        {
            string s;
            for(int i=0;i<tmp.size()-1;i++)//将前n-1个节点加入，中间需要到->符号
            {
                s+=to_string(tmp[i]);
                s+="->";
            }
            s+=to_string(tmp[tmp.size()-1]);//单独添加最后一个节点
            arr.push_back(s);
        }
        if(root->left)//模拟回溯函数，先增加节点，然后删除节点
        {
            Allpath(root->left,tmp);
        }
        if(root->right)
        {
            Allpath(root->right,tmp);
        }
        tmp.pop_back();
    }
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<int> tmp;
        Allpath(root,tmp);
        return arr;
    }

404. 左叶子之和

题意：给定二叉树的根节点 root ，返回所有左叶子之和。

示例：

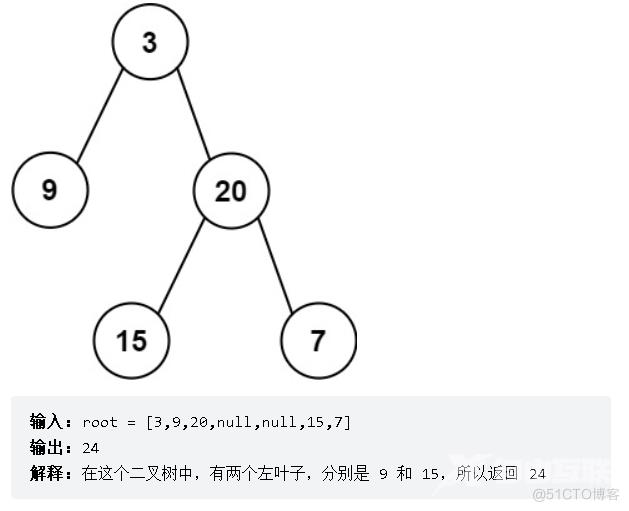
       思路：本题我们需要考虑的是，什么是左叶子？即叶子节点的上一个节点的左孩子，就是左叶子。因此，我们需要使用中序便利的方法，找到左叶子，然后再根据左叶子的判断条件进行相加即可

C++代码：

int sum=0;
    void CountLeft(TreeNode* root)
    {
        if(root->left)//中序遍历写法，我们永远需要的都是左叶子节点，包括右子树，也是左叶子节点
        {
            CountLeft(root->left);
        }
        if(root->left!=nullptr&&root->left->left==nullptr&&root->left->right==nullptr)//判断是否为左叶子
        {
            sum+=root->left->val;
        }
        if(root->right)
        {
            CountLeft(root->right);
        }
    }
    int sumOfLeftLeaves(TreeNode* root) {
        CountLeft(root);
        return sum;
    }