在一个有序数组中,采用二分法查找目标数字。
【注意】数组必须是有序的。
1.采用二分法的优势
比如一个数组
arr[]={1,2,3,4,5,6,7,8,9,10}如果采用遍历法查找某一个数,我们最多可能要进行 10 次的查找,而采用二分法却能极大的减少这个次数。
10 次看起来似乎也不算太多,但是在解决实际问题的过程中,我们可能会碰到更加复杂多样的情况,需要处理的数据可能成百上千,甚至更多,在这些情况下二分法的优势就极大的体现了出来。
采用二分法可以极大的提高我们程序的运行效率。
2.二分法的实现
首先,我们先定义一个有序数组:
int arr[] = { 1,2,3,4,5,6,7,8,9,10 };刚开始时,两端的元素分别为:
arr[0] 与 arr[9],下标为 0 和 9 。
分别定义 left 和 right 用来存储左右两端元素的下标:
int left = 0;
int right = sizeof(arr) / sizeof(arr[0]) - 1;
其中,sizeof(arr)/sizeof(arr[0]) 用来计算数组中元素的个数,而数组中元素的个数减一,则为最末端元素的下标,所以 right = sizeof(arr) / sizeof(arr[0]) - 1
定义 mid 来储存中间元素下标:
int mid = 0;关于希望查找的数字,我们可以自定义赋值,或者由 scanf 函数输入。
(1)自定义赋值
int k = 7;(2) scanf 函数输入
printf("请输入要查找的数k=");
scanf("%d", &k);接下来我们进入主体部分:
mid = (left + right) / 2;//由两端元素,获取中间元素的下标值
if (arr[mid] < k)//第一种情况,中间值小于查找值
{
left = mid + 1;//左端元素往右移,为mid+1
//右端元素不变
}
else if (arr[mid] > k)//第二种情况,中间值大于查找值
{
right = mid - 1;;//右端元素往左移,为mid+1
//左端元素不变
}
else //第三种情况,中间值等于查找值
{
printf("该数为arr[%d]\n", mid);//找到该数
break; //结束循环
}完整代码,如下:
#include <stdio.h>
int main()
{
int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
int left = 0;
int right = sizeof(arr) / sizeof(arr[0]) - 1;
int mid = 0, k;
printf("请输入要查找的数k=");
scanf("%d", &k);
while (left <= right)
{
mid = (left + right) / 2;
if (arr[mid] < k)
{
left = mid + 1;
}
else if (arr[mid] > k)
{
right = mid - 1;
}
else
{
printf("该数为arr[%d]\n", mid);
break;
}
}
if (left > right)
printf("该数不在数组中");
return 0;
}运行结果为:
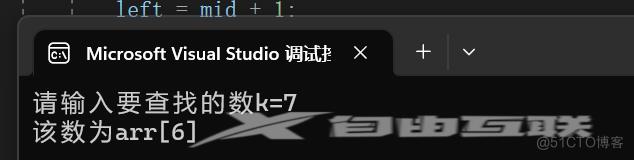
在上面的 while 循环中,循环执行条件为 left<=right , 关于这一点至关重要。
什么时候,循环执行或者结束,在执行上面程序的时候,我们需要思考,如果我们需要查找的数,不存在于数组中时,我们的程序又该如何处理。
在多次循环查找之后,如果出现了 left = right 的情况,此时 mid =left = right,此时仍然未出现 arr[mid] = k 的情况,继续执行下去,left 和 right 的值将会进行交错,即 left>right,说明数组中不存在查找的数。
所以,我们用下面代码进行选择调试:

运行结果:

至此,我们就实现了二分查找算法的实现。
