最大m子段和
一、定义
给定由n个整数(可能为负)组成的序列a1、a2、a3...,an, 以及一个正整数m,要求确定序列的m个不相交子段,使这m个子段的总和最大!
特别注意:有些题目可能不存在负数答案,给出的序列全是负数,那么不管m是多少,答案是0。此时选择的子段是0个,不足m个,但符合题意。。。也可能有些题目要求,必须选够m个子段。区别在dp数组的初始化。前者要求dp初始为0,后者要求第0行为0,其余为负无穷
二、解题思路
动态规划,借助矩阵可以直观的看到计算过程。
定义二维数组dp, dp[ i ][ j ],表示前 j 项所构成 i 子段的最大和,且必须包含着第j项,即以第j项结尾
然后是一个递推过程。
求dp[ i ][ j ],有两种情况
dp[ i ][ j ] = dp[ i ] [ j-1 ] + a[ j ]
dp[ i ][ j ] = dp[ i-1 ] [ t ] + a[ j ],(i-1<= t < j ),把第 j 项作为单独的一个子段,然后找一下i-1个子段时,最大的和,然后加上a[ j ]
然后比较上面两种情况,取大的。
下面看图,红色数字为输入的序列:
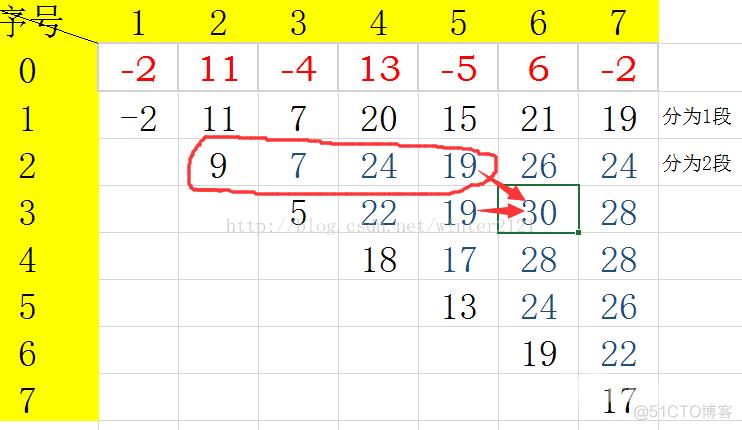
他左边的那个,和上面那一行圈起来的之中 最大的数,
再加上a[ j ] 即为dp[ 3 ][ 6 ] 的值。
优化一下:
1、沿着第m行的最后一个元素,往左上方向画一条线,线右上方的元素是没必要计算的
那么dp[ i ][ j ] ,j++的时候,j的上限为 i + n - m 即可。
还有左下角那一半矩阵,也是不用计算的,因为1个数字不可能分为2个子段
本行和上一行,所以不用开维数组也可以,省内存。
开两个一维数组,pre和dp,pre记录上一行,dp记录当前行
3、再对上一行红圈中的数字找最大值时,若用一个循环来找,容易超时。所以优化方法是:在每次计算dp之前,同时记录下j前面的最大元素。
时间复杂度大致为O(m*(n-m+1)),mn-m方
通过图片,分析情况1和2,就能发现,从左上角走到第 m 行的最后一个元素即可,找出第 m 行的最大值即为答案。
详见例题。
三、例题
51nod 1052
1052 最大M子段和
N个整数组成的序列a[1],a[2],a[3],…,a[n],将这N个数划分为互不相交的M个子段,并且这M个子段的和是最大的。如果M >= N个数中正数的个数,那么输出所有正数的和。
例如:-2 11 -4 13 -5 6 -2,分为2段,11 -4 13一段,6一段,和为26。
Input
第1行:2个数N和M,中间用空格分隔。N为整数的个数,M为划分为多少段。(2 <= N , M <= 5000)
第2 - N+1行:N个整数 (-10^9 <= a[i] <= 10^9)
Output
输出这个最大和
Input示例
7 2
-2
11
-4
13
-5
6
-2
Output示例
26
【AC代码】:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+5;
const int INF=0x3f3f3f3f;
int n,m;
ll a[N],dp[2][N]; //只保存上一行和当前行
int main()
{
while(~scanf("%d%d",&n,&m)) //n个数字,m子段和
{
for(int i=1;i<=n;i++)
scanf("%lld",a+i);
for(int i=0;i<=n;i++)
dp[0][i]=0,dp[1][i]=0; //关键!此题答案只允许正值
for(int i=1,k=1;i<=m;i++,k^=1) //分为i段,k为两行之间的切换
{
dp[k][i-1]=-INF; //i==j时,杜绝与前一元素共伍
ll maxpre=-INF; //maxpre记录上一行的最大值
for(int j=i;j<=n-m+i;j++)
{
maxpre=max(maxpre,dp[k^1][j-1]); //随时更新上一行最大值
dp[k][j]=max(dp[k][j-1],maxpre)+a[j]; //*对情况1、2的选择
}
}
ll ans=-INF;
for(int i=m;i<=n;i++) //找到第m行的最大值,即为答案
ans=max(ans,dp[m&1][i]);
printf("%lld\n",ans);
}
}数据量比51nod的这个题大,一百万。上面的代码,把n和m互换就可以过HDU1024
