前缀和与差分

持续创作，加速成长！这是我参与「掘金日新计划 · 10 月更文挑战」的第32天，点击查看活动详情

1、一维数组的前缀和

对于一个数列 a1,a2,a3,a4····an，前缀和Si就是前i项的代数和。 所以在用数组储存数列的时候我们不使用a[0]，这样我们就可以令S[0]=0。

#include <iostream>
#include <string>
using namespace std;
const int N = 10000;
int n, m;
int a[N], s[N] = {0};
int main()
{
	scanf_s("%d%d", &n, &m);
	for (int i = 1; i <= n; i++) scanf_s("%d", &a[i]);
	for (int i = 1; i <= n; i++) 
            s[i]=s[i-1]+a[i];//前缀和的初始化
            //S[1]=S[0]+a[1];不使用a[0]的好处！！！！
	//while (m--)
	//{
		int l, r;
		scanf_s("%d%d", &l, &r);
		printf("%d\n", s[r] - s[l - 1]);//区间和的计算
	//}
}

2、二维数组的前缀和

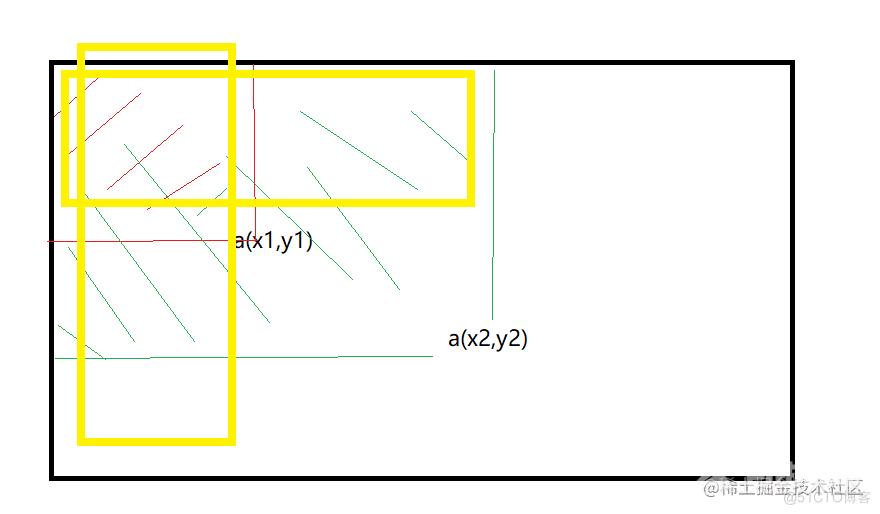
和一位数组的思想一样，二维数组的前缀和指的是从（0，0）->（i，j）子组数的和。 如图所示a(x1,y1)的前缀和是红色区域所有的代数和，a(x2,y2)的前缀的是绿色区域所有的代数和。 如此一来由前缀和组成的与原数组同形数组被称为前缀和数组。我们要做的是求原数组某个子数组的代数和，我们可以先求出这个原数组的前缀和数组，再求子数组代数和。

// int sum = S[x2][y2] + S[ x1 - 1][ y1 - 1] - S[x1 - 1][ y2] - S[x2][y1 - 1];

//子二维数组和
#include <iostream>
//#include <stdio.h>
#include <string>
using namespace std;
const int N = 10000, M = 10000;
int arr[N][M] = { 0 };
int S[N][M] = { 0 };
int n, m;
int Sum(int arr[][M],int x, int y)
{
	int sum = 0;
	for (int i = 1; i <= x; i++) {
		for (int j = 1; j <= y; j++) {
			sum += arr[i][j];		
		}
	}
	for (int i = 1; i <= x; i++) {
		for (int j = 1; j <= y; j++) {
			S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + arr[i][j];
		}
	}
	return sum;
}
int main()
{
	
	scanf_s("%d%d", &n, &m);
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			scanf_s("%d", &arr[i][j]);
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + arr[i][j];
		}
	}
	int x1=2, x2=4, y1=2, y2=4;
	int sum = S[x2][y2] + S[ x1 - 1][ y1 - 1] - S[x1 - 1][ y2] - S[x2][y1 - 1];
	printf("%d", sum);
}

3、一维数组的差分

int a[n], b[n];//原数组与差分数组 差分和前缀和是一对逆运算： 原数组经过前缀和得到前缀和数组，前缀和数组经过差分得到原数组。 这样一来如果我们相对原数组的某个区间[i,j]的元素都加上同一个数c,我们直接 b[l] += c; b[r + 1] -= c;就ok了。

//差分算法
#include <iostream>
#include <string>
using namespace std;
const int n = 10000;
int n, m;
int a[n], b[n];//原数组与差分数组
void inster(int l, int r, int c)
{
	b[l] += c;
	b[r + 1] -= c;
}
int main()
{
	scanf_s("%d", &n);
	for (int i = 1; i <= n; i++) {
		scanf_s("%d", &a[i]);
	}
	for (int i = 1; i <= n; i++) {
		inster(i, i, a[i]);
	}//构造差分数组 
	int l, r, c;
	scanf_s("%d%d%d", &l, &r, &c);//l-r之间加c
	inster(l, r, c);
	for (int i = 1; i <= n; i++)
		b[i] += b[i - 1];
	for (int i = 1; i <= n; i++) 
		printf("%d ", b[i]);
}

4、二维数组的差分

int a[N][N], b[N][N];//a[N][N]为原数组，b[N][N]为差分数组 二位数的差分作用也是一样的，目的是对原二维数组的某个子数组同时进行加上某个数。如若通过遍历二维数组来操作，就是O(n^2)的时间复杂的，但是用差分数组就是：b[x1][y1] += c; b[x2 + 1][y1] -= c; b[x1][y2 + 1] -= c; b[x2 + 1][y2 + 1] += c;即可。O(1)的时间复杂度。

//二位差分
#include<iostream>
using namespace std;
const int N = 10000;
int n, m, q;
int a[N][N], b[N][N];
void inster(int x1, int y1, int x2, int y2, int c)
{
	b[x1][y1] += c;
	b[x2 + 1][y1] -= c;
	b[x1][y2 + 1] -= c;
	b[x2 + 1][y2 + 1] += c;
}
int main()
{
	scanf_s("%d%d%d", &n, &m, &q);
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++)
		{
			scanf_s("%d", &a[i][j]);
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++)
		{
			inster(i, j, i, j, a[i][j]);
		}
	}
	int x1, y1, x2, y2, c;
	scanf_s("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
	inster(x1, y1, x2, y2, c);

	for (int i = 1; i <= n; i++) {//求前缀和
		for (int j = 1; j <= m; j++)
			b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
	}

	for (int i = 1; i <= n; i++) {//求前缀和
		for (int j = 1; j <= m; j++)
			printf("%d ", b[i][j]);
		printf("\n");
	}
}