解决思路 如果是空树,则深度为0; 否则,递归计算左子树的深度记为m,递归计算右子树的深度记为n,二叉树的深度则为m与n的较大者加1。 int Depth(BiTree T){ if(T==NULL) return 0; else { m=Dept
解决思路
如果是空树,则深度为0;
否则,递归计算左子树的深度记为m,递归计算右子树的深度记为n,二叉树的深度则为m与n的较大者加1。
int Depth(BiTree T)
{
if(T==NULL)
return 0;
else
{
m=Depth(T->lchild);
n=Depth(T->rchild);
if(m>n)
return (m+1);
else
return (n+1);
}
}代码测试
#include<stdio.h>
#include<stdlib.h>
#define OVERFLOW -2
#define OK 1
#define ERROR 0
typedef int Status;
typedef char TElemType;
typedef struct BiTNode
{
TElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
Status CreateBiTree(BiTree *T)
{
char ch;
ch=getchar();
if(ch=='#')
*T=NULL;
else
{
(*T)=(BiTNode*)malloc(sizeof(BiTNode));
if(!*T)
exit(OVERFLOW);
(*T)->data=ch;
CreateBiTree(&(*T)->lchild);
CreateBiTree(&(*T)->rchild);
}
return OK;
}
Status PreOrderTraverse(BiTree T,Status (*visit)(TElemType e))
{
if(T)
{
(*visit)(T->data);
PreOrderTraverse(T->lchild,visit);
PreOrderTraverse(T->rchild,visit);
}
else
return OK;
}
Status InOrderTraverse(BiTree T,Status (*visit)(TElemType e))
{
if(T)
{
InOrderTraverse(T->lchild,visit);
(*visit)(T->data);
InOrderTraverse(T->rchild,visit);
}
else
return OK;
}
Status PostOrderTraverse(BiTree T,Status (*visit)(TElemType e))
{
if(T)
{
PostOrderTraverse(T->lchild,visit);
PostOrderTraverse(T->rchild,visit);
(*visit)(T->data);
}
else
return OK;
}
Status visit(TElemType e)
{
printf("%c\t",e);
return OK;
}
int Depth(BiTree T)
{
int m,n;
if(T==NULL)
return 0;
else
{
m=Depth(T->lchild);
n=Depth(T->rchild);
if(m>n)
return (m+1);
else
return (n+1);
}
}
int main()
{
BiTree T;
char ch;
int n;
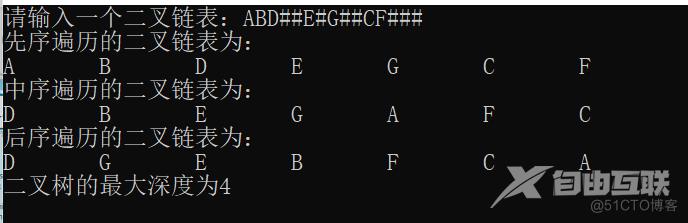
printf("请输入一个二叉链表:");
CreateBiTree(&T);
printf("先序遍历的二叉链表为:\n");
PreOrderTraverse(T,visit);
printf("\n");
printf("中序遍历的二叉链表为:\n");
InOrderTraverse(T,visit);
printf("\n");
printf("后序遍历的二叉链表为:\n");
PostOrderTraverse(T,visit);
printf("\n");
n=Depth(T);
printf("二叉树的最大深度为%d\n",n);
return 0;
}