作者丨苹果姐
编辑丨3D视觉工坊
在自动驾驶实际应用中,对相机传感器的要求之一是拥有尽可能大的视野范围,鱼眼相机由于视场角(FOV)极大(标准镜头45°左右,广角镜头可大于60°,鱼眼相机可大于180°,也就是说甚至可以看到镜头后面的场景),在自动驾驶汽车上广泛使用。所以如何直接从鱼眼相机图像中估计深度是自动驾驶实际落地的一个重点问题。
然而鱼眼相机的大FOV带来的是非常大的非线性畸变,这决定了相比一般针孔相机,鱼眼相机图像的深度估计方法将更加复杂。虽然一个思路是对畸变进行矫正后再进行深度估计,但校正必定会引起FOV的缩小,失去使用鱼眼相机的意义,所以直接从鱼眼相机原图进行深度估计是学术界研究的热点问题。目前Valeo公司在鱼眼图像深度估计的研究中处于领先地位,博主之前对该公司的一系列成果做过一个简要综述:https://zhuanlan.zhihu.com/p/495899515
该公司的github地址是:https://github.com/rvarun7777,核心代码都存放在omnidet路径下,但与论文omnidet[1]中描述的内容差距较大,仅开放了distance/detection/semantic/motion四个独立任务以及联合多任务的基线版本,其中distance任务即鱼眼深度估计任务,相比FisheyeDistanceNet[2],并没有使用可变卷积、超分辨率网络、速度监督信号、交叉一致性损失等trick,而是仅保留了和monodepth2[3]一致的重投影ssim+l1损失以及平滑损失,但重投影部分是鱼眼图像深度估计的核心,还是值得我们深入学习。以下进行相关部分的原理分析和核心代码解读:
[1]OmniDet: Surround View Cameras based Multi-task Visual Perception Network for Autonomous Driving (ICRA 2021)
[2] FisheyeDistanceNet: Self-Supervised Scale-Aware Distance Estimation using Monocular Fisheye Camera for Autonomous Driving (ICRA 2020)
[3] Digging Into Self-Supervised Monocular Depth Estimation (ICCV 2019)
首先,从大的理论上,鱼眼图像自监督深度估计和针孔图像自监督深度估计一致,都是采用sfm-learner[4]的方法:
[4] Unsupervised Learning of Depth and Ego-Motion from Video (CVPR 2017)
即利用视频连续帧图像之间的重投影对位姿和深度的约束,来实现网络对深度和位姿的学习。本文假设读者已掌握针孔图像重投影的原理,如果不甚了解请先阅读博主的以下文章:https://zhuanlan.zhihu.com/p/462656351
现在正式进入鱼眼图像自监督深度估计内容。
一、鱼眼相机成像模型
关于鱼眼相机成像模型,可以参考博主以下文章:https://zhuanlan.zhihu.com/p/456538243
整个模型可以通过下图表示:
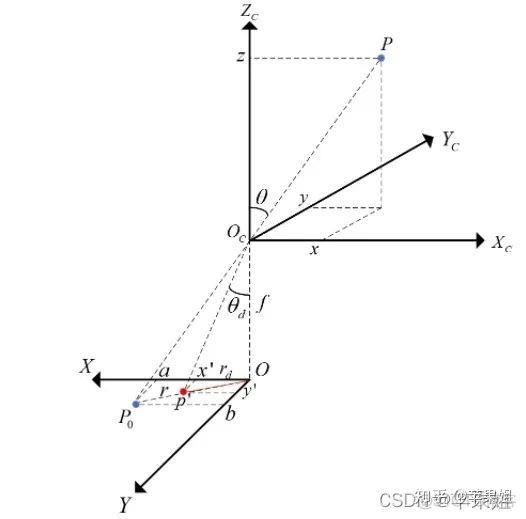
点P为空间中的一点,Oc为鱼眼相机的光心,Oc-XcYcZc为鱼眼相机坐标系。OcP和z轴的夹角为θ,也称为入射角。P经过Oc后在焦距为f的像平面上成像,由于鱼眼相机的畸变,点P在图像坐标系OXY中的投影不在直线传播的Po上,而是在经过折射的p'上。p'到图像坐标系原点O的距离为rd。鱼眼相机的畸变公式:
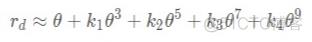
描述了rd和θ的关系,即可以将3D与2D联系起来,实现3D到2D坐标的互相转换。要注意的是因为这个折射关系与焦距f无关,所以为了简便,畸变公式描述的rd是归一化像平面上p'到O的距离。所以在实际计算中,还需要通过相机的内参,转换到焦距为f的像平面上的像素坐标系的坐标u,v。
了解了鱼眼相机成像模型,我们可以较容易地实现重投影过程。
二、重投影之2D到3D投影
首先进行的是target帧图像2D坐标到3D坐标的投影,即已知像素坐标[u, v],求3D坐标[X, Y, Z]。这里需要的输入参数为内参矩阵K、畸变系数列表D、distance网络的输出深度值distance(d)。这里值得指出的是,FisheyeDistanceNet[2]输出的并不是目标点到相机平面的垂直距离depth,而是目标点到相机光心的距离distance([X, Y, Z]的二范数),二者在上图中的关系是:depth = distance * cos(θ)。论文中未详细解释这样做的原因,可能是因为distance更加直观地符合自动驾驶应用场景。但博主考虑到由于distance是与位置相关的,为了让网络更好地学到位置,可能应该考虑加入位置编码信息,这点值得深入探索。
在2D到3D投影过程中,我们容易得到的是rd,而rd又在归一化像平面上,所以求rd的步骤为:
a.用np.meshgrid函数得到h*w分辨率的像素坐标系坐标[u, v]
b.像素坐标系经过内参矩阵,转换为归一化像平面坐标[x, y]
c.对[x, y]求二范数即为rd, 同时可以求得x,y在像平面的夹角φ
求得rd后,即可使用畸变公式求得θ:
d.使用np.root函数和畸变参数列表D、rd,求解得到θ矩阵。
Omnidet中这部分的代码为:
# Scale intrinsics to adjust image resize.
K, D = scale_intrinsic(args, intrinsic, coords)
x = np.linspace(0, args.input_width - 1, args.input_width)
y = np.linspace(0, args.input_height - 1, args.input_height)
mesh_x, mesh_y = np.meshgrid(x, y)
mesh_x, mesh_y = mesh_x.reshape(-1, 1), mesh_y.reshape(-1, 1)
x_cam = (mesh_x - K[1]) / K[0]
y_cam = (mesh_y - K[2]) / K[0]
r = np.sqrt(x_cam * x_cam + y_cam * y_cam)
theta_LUT = np.arctan2(y_cam, x_cam).astype(np.float32)
angle_LUT = np.zeros_like(r, dtype=np.float32)
for i, _r in tqdm(enumerate(r)):
a = np.roots([D[3], D[2], D[1], D[0], -_r])
a = np.real(a[a.imag == 0])
try:
a = np.min(a[a >= 0])
angle_LUT[i] = a
except ValueError: # raised if `a` is empty.
print(f"Field angle of incident ray is empty")
pass
在求θ(代码中的angle_LUT))过程中,由于np.roots函数返回的既有实数根又有复数根,所以需要过滤掉复数根,并且选取正的最小值(θ范围为0~FOV/2)。而且由于这个步骤耗时较长,而且是固定值,只需要计算一次,所以可以先离线计算出θ矩阵,在训练阶段直接使用。
得到θ和φ后,再根据distance网络输出的距离值d,即可得到P点在相机坐标系下的3D坐标[X, Y, Z]:
e.根据几何关系可得:
Z = d * cos(θ)
X = d * sin(θ)* cos(φ)
Y = d * sin(θ)* sin(φ)
三、重投影之3D到2D投影
求得target帧图像的3D坐标值[X, Y, Z]后,需要再通过posenet网络输出的pose信息,转换到source帧图像的3D坐标值,再投影到source帧图像的像素坐标系得到对应的像素坐标值[u, v],完成图像重构。
其中3D到2D投影的过程是第二节的逆过程:
a.根据3D坐标值[X, Y, Z],可求得r,φ, θ:
φ = arctan(Y/ X)
r = sqrt(X^2 + Y^2)
θ = arctan(r / Z)
b.根据畸变公式、畸变系数矩阵D和θ,可以求得rd
c.根据rd, r, φ, 可以求得归一化像平面坐标[x, y]:
x = rd * cos(φ)
y = rd * sin(φ)
d.根据内参矩阵K,可以求得焦平面像素坐标系坐标[u, v]
Omnidet中这部分的代码为:
x_cam, y_cam, z = [world_coords[:, i, :].unsqueeze(1) for i in range(3)]
# angle in the image plane
theta = torch.atan2(y_cam, x_cam)
# radius from angle of incidence
r = torch.sqrt(x_cam * x_cam + y_cam * y_cam)
# Calculate angle using z
a = np.pi / 2 - torch.atan2(z, r)
distortion_coeffs = distortion_coeffs.unsqueeze(1).unsqueeze(1)
r_mapping = sum([distortion_coeffs[:, :, :, i] * torch.pow(a, i + 1) for i in range(4)])
intrinsics = intrinsics.unsqueeze(1).unsqueeze(1)
x = r_mapping * torch.cos(theta) * intrinsics[:, :, :, 0] + intrinsics[:, :, :, 2]
y = r_mapping * torch.sin(theta) * intrinsics[:, :, :, 1] + intrinsics[:, :, :, 3]
四、图像重构和求损失函数
得到target帧图像在source帧图像中对应的像素坐标后,即可通过F.grid_sample函数完成图像重构,进而计算l1损失、SSIM损失、平滑损失等,因为与monodepth2[3]类似,本文不再赘述。
五、激光点云真值投影与模型评测
同样由于distancenet输出的是点P到光心的距离D,所以在模型评测时需要根据事先保存的θ矩阵先转换成深度值d,再与激光点云投影得到的gt深度图进行对比评测:
d = D * cos(θ)
其中点云投影过程与第三节过程相似,只是在生成gt深度图的时候有自己特殊的处理:
a. 已知激光点云坐标[X, Y, Z], 通过外参矩阵T转换到相机坐标系坐标[x, y, z]
b. 执行第三节的a-d步骤,但保留z坐标,得到像素坐标系坐标[u, v, z]
c.按照h*w分辨率初始化深度图gt_depth(h*w*1),过滤掉超出边界的坐标、z<0的坐标
d.由于分辨率的限制,和雷达与相机视角不同的影响,可能存在多个点映射到同一个像素坐标的情况,只保留深度值z最小的点。
e.根据d和gt_depth进行相关指标的评测
注:由于c、d步骤中的过滤操作并不影响图像重构(target帧多个点映射到source帧同一个点的情况),所以在第三节中并不需要进行过滤。
具体实现请参照monodepth2代码中generate_depth_map方法,并自行扩充到鱼眼相机投影模型。
至此,关于鱼眼图像自监督深度估计原理分析和核心代码解读告一段落,希望读者留言交流。
本文仅做学术分享,如有侵权,请联系删文。
