1. 前言
什么是树型动态规划?
概念中有 2 个子概念:
- 一个是动态规划概念。动态规划可以简单理解为通过对已经计算出来的
子问题的状态值进行修改(基于子问题的状态值找到当前子问题的最优值)而得到当前子问题的状态值。
Tips: 本文侧重于动态规划在树型结构中的应用,更多关于动态规划的基础理论和常规知识,可以翻阅相关资料。
树指树数据结构。树型动态规划算法指在树逻辑结构之上提供的动态规划思想。
动态规划最重要环节查找到子问题间发生变化的状态量以及状态转移表达式。树型动态规划的状态转移过程一般都是由子树向根结点转移,这也符合动态规划的由底向上的逻辑思想。
本文通过讲解几个经典的树型动态规划案例,揭开其神秘面纱。
2. 经典案例
2.1 没有上司的舞会
没有上司的舞会是树型动态规划最经典的案例。下文将剖析此案例的细节,从而深度理解树型动态规划的逻辑流程。
问题描述:
某公司有 n 个职员,编号为 1∼N。公司吗,必然存上、下级关系。员工之间的关系从逻辑结构而言,就是典型的树结构。
在树结构中,父结点是子结点的直接上司。如下图所示:
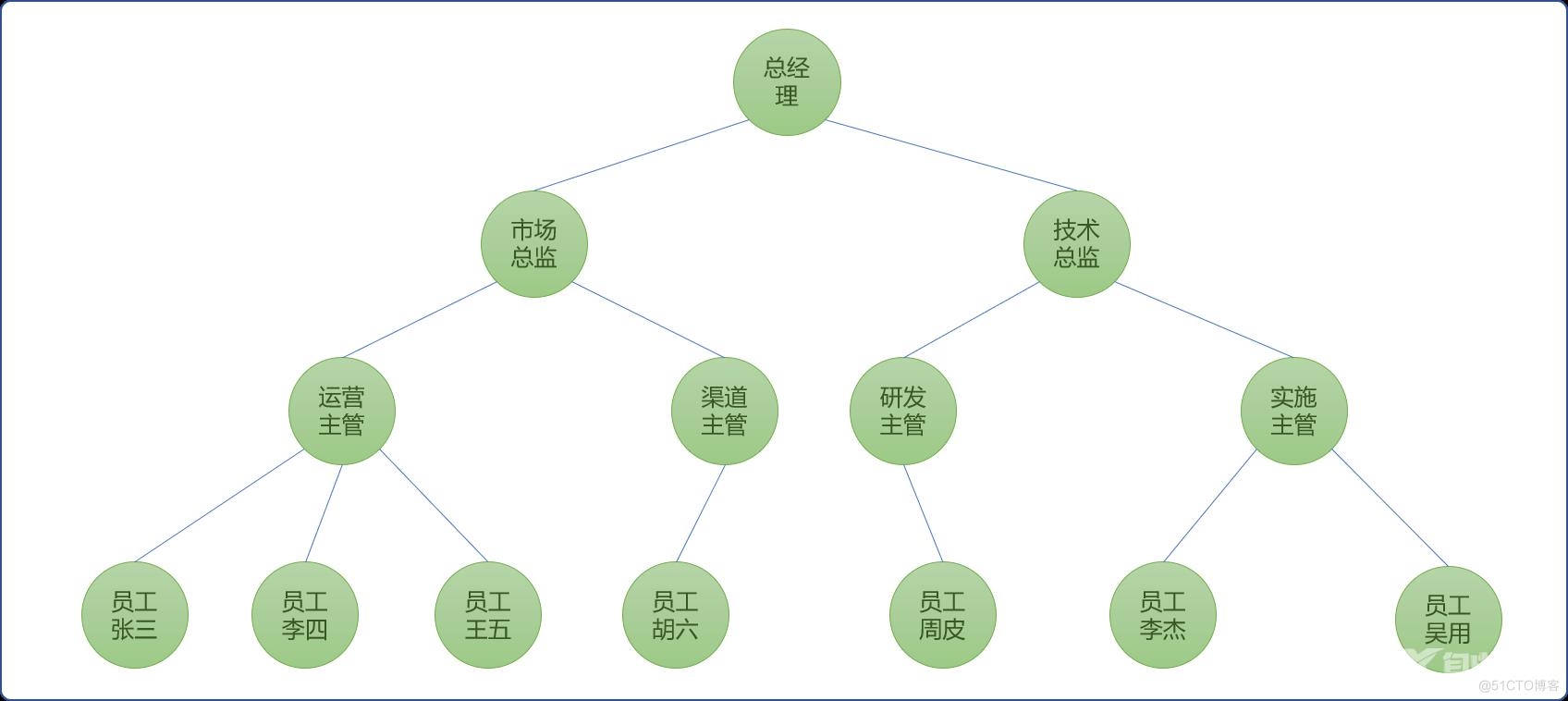
现在有个联欢舞会会,每邀请来一个职员都会给舞会增加一定的快乐指数,但是,如果某个员工的上司来参加舞会了,那么这个职员不会过来参加舞会。
题目要求,邀请哪些员工可以使整个舞会的快乐指数最大。
问题分析:
分析题目可得到如下的的一些信息:
第一: 每一个员工都有一个权重:快乐指数。如下图,节点括号内数字表示快乐指数。
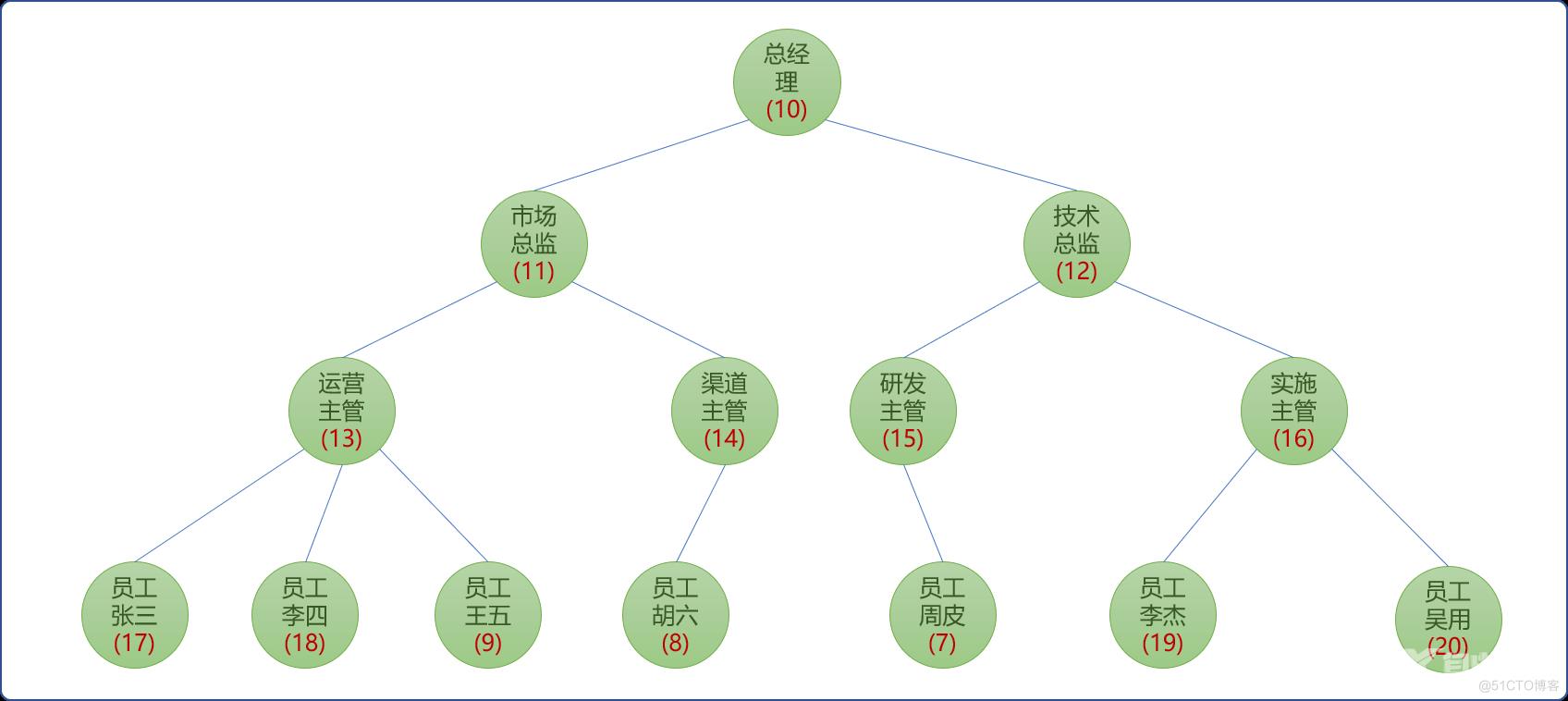
第二: 此问题是否能使用动态规划算法思想?
动态规划要求有子问题且须有最优子结构。
树结构本身就是树和子树的逻辑结构,子问题是天然存在的。- 至于有没有最优子结构,可以把问题规模先缩小。
如下图所示,现在是一个上司两个下属。
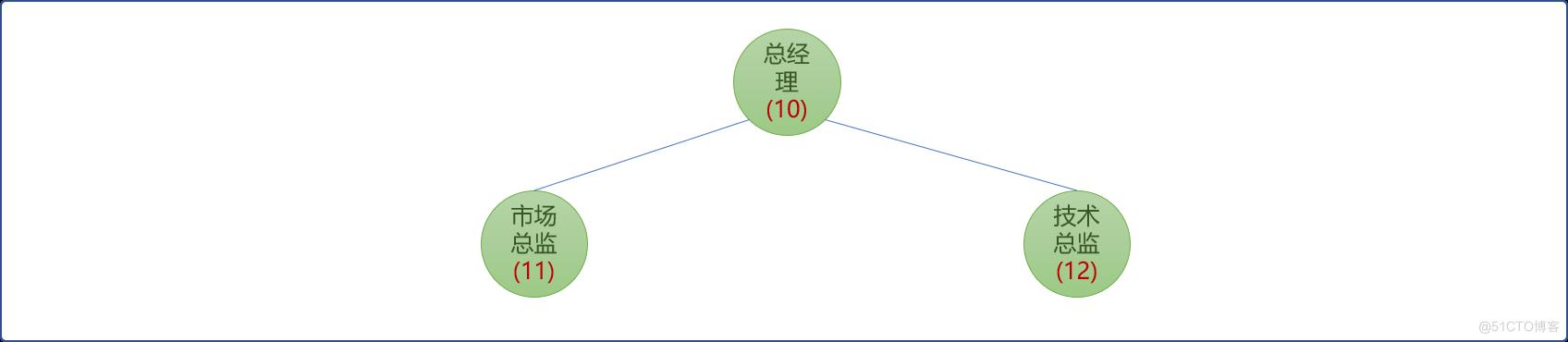
站在邀请方可有 2 种方案:
- 邀请
总经理节点,因此节点是树中其它2个节点的父节点,一旦邀请它,子结点不会参加。此时的快乐指数为10。此种方案是不是最优方案,现还不能下结论。 - 不邀请
总经理,显然市场总监的最优值是11,技术总监的最优值是12。 邀请市场总监和技术总监后快乐指数为23。
从现状而言(仅3 个节点),显然选择不邀请父结点能得到最大快乐指数:23。
通过分析可知:
当知道子结点的最优值后可以判断出当前结点的最终结论(是去得到最大值还是不去得到最大值)。所以,此问题是存在最优子结构的,并且符合动态规划的由下向上的求解思想。
基于动态规划思想,先计算最底层节点的最优快乐指数,然后一层一层向上更新父节点的快乐指数。最终得到问题的最优解。如下图所示:
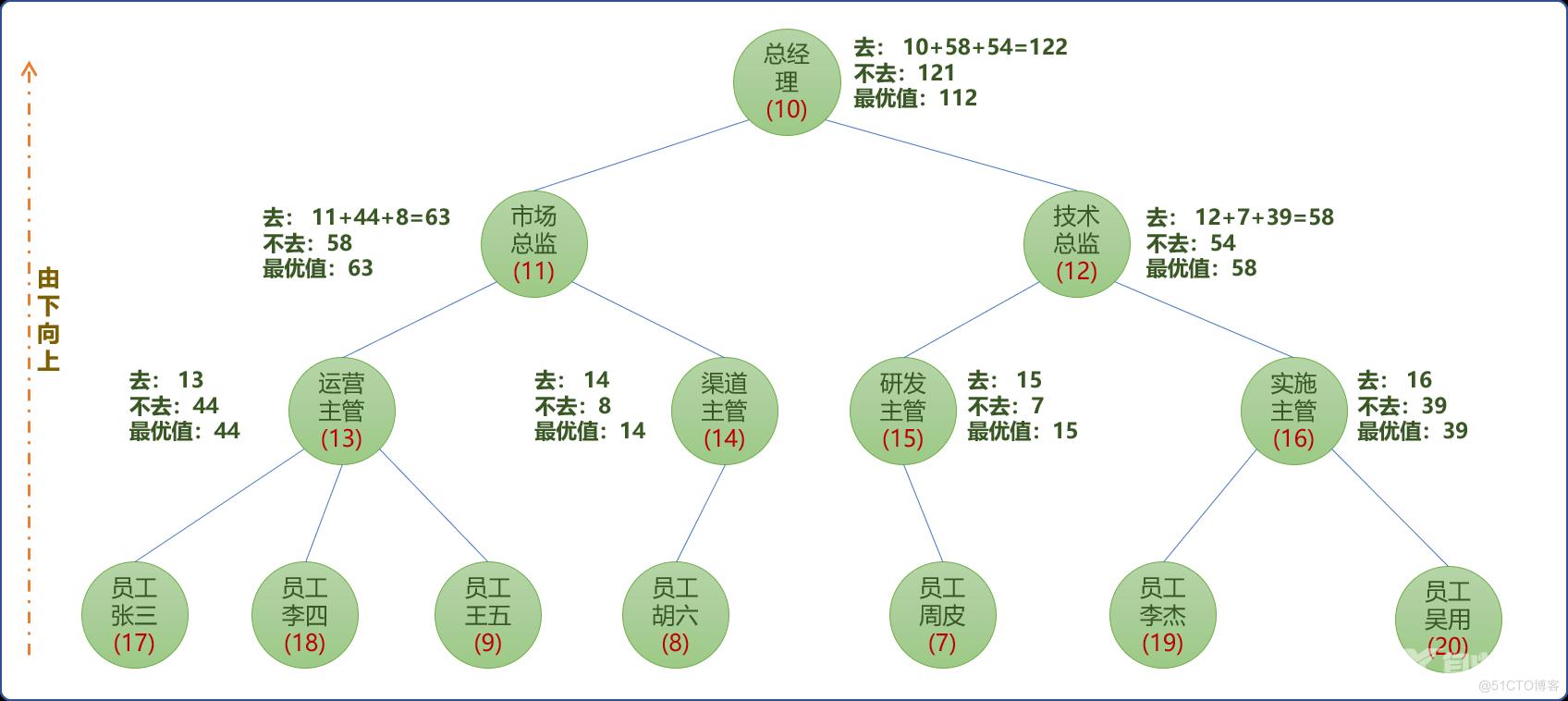
对于任何一个节点而言,都会有 2 个最优状态值。
- 如果去:提供的快乐指数就是自身指数加上子节点不去时的快乐指数值。
- 如果不去:自身快乐指数加上子节点去还是不去两者间的较大值。
可以借助一个二维数组存储每个节点的状态值。

编码实现:
编码的核心逻辑:
- 使用
DFS(深度搜索)算法由叶节点最优值向上更新至父节点的最优值。 - 更新(状态)值存储在二维状态
(dp)数组中。
设计流程:
#include <iostream>
#include <vector>
using namespace std;
/*
*节点类
*/
struct Emp {
//员工编号
int empId;
//员工姓名
string empName;
//权重:快乐指数
int happy;
Emp() {
}
Emp(int empId,string empName,int happy) {
this->empId=empId;
this->empName=empName;
this->happy=happy;
}
};
没有上司的舞会封装类:
/*
*树(舞会)类
*/
class Dance {
private:
//使用一维数组存储所有员工
Emp emps[100];
//存储员工之间的从属关系
vector<int> relationship[100];
//员工数量
int empCount;
//员工编号,内部维护
int num;
//二维状态数组,行号为员工编号
int happys[100][2];
public:
Dance() {
}
Dance(int empCount) {
this->num=0;
//员工数量
this->empCount=empCount;
}
/*
* 添加新员工
* 返回员工的编号
*/
int addEmp(string empName,int happy) {
Emp emp(this->num,empName,happy);
this->emps[this->num]=emp;
return this->num++;;
}
/*
*添加员工之间从属关系
*/
void addRelation(int from,int to) {
this->relationship[from].push_back(to);
}
/*
*规定编号为 0 的员工为根节点
*/
int getRoot() {
return 0;
}
/*
* 深度搜索实现
*树型动态规划
*/
void treeDp(int empId) {
//不去
happys[empId][0]=0;
//去
happys[empId][1]=this->emps[empId].happy;
for(int subEmpId: this->relationship[empId]) {
//基于子节点深度搜索
treeDp(subEmpId) ;
//搜索完毕 ,更新状态值,如果不去,查找子节点去与不去的最大值
happys[empId][0] += max(happys[subEmpId][0],happys[subEmpId][1]);
//去,添加子节点不去时的状态值
happys[empId][1]+=happys[subEmpId][0];
}
}
/*
*输出状态值
*/
void maxHappy() {
cout<<"各节点的快乐指数状态值:"<<endl;
for(int i=0; i<this->num; i++) {
for(int j=0; j<2; j++) {
cout<<this->happys[i][j]<<"\t";
}
cout<<endl;
}
cout<<"最大快乐指数:"<< max(this->happys[0][0],this->happys[0][1] )<<endl;
}
};
测试:
int main() {
Dance dance(14);
int root= dance.addEmp("总经理",10) ;
int sczj= dance.addEmp("市场总监",11) ;
dance.addRelation(root,sczj);
int jszj= dance.addEmp("技术总监",12) ;
dance.addRelation(root,jszj);
int yyzg= dance.addEmp("运营主管",13) ;
dance.addRelation(sczj,yyzg);
int qdzg= dance.addEmp("渠道主管",14) ;
dance.addRelation(sczj,qdzg);
int yfzg= dance.addEmp("研发主管",15) ;
dance.addRelation(jszj,yfzg);
int sszg= dance.addEmp("实施主管",16) ;
dance.addRelation(jszj,sszg);
int yg= dance.addEmp("员工张三",17) ;
dance.addRelation(yyzg,yg);
yg= dance.addEmp("员工李四",18) ;
dance.addRelation(yyzg,yg);
yg= dance.addEmp("员工王五",9) ;
dance.addRelation(yyzg,yg);
yg= dance.addEmp("员工胡六",8) ;
dance.addRelation(qdzg,yg);
yg= dance.addEmp("员工周皮",7) ;
dance.addRelation(yfzg,yg);
yg= dance.addEmp("员工李杰",19) ;
dance.addRelation(sszg,yg);
yg= dance.addEmp("员工吴用",20) ;
dance.addRelation(sszg,yg);
dance.treeDp(root);
dance.maxHappy();
return 0;
}
输出结果:
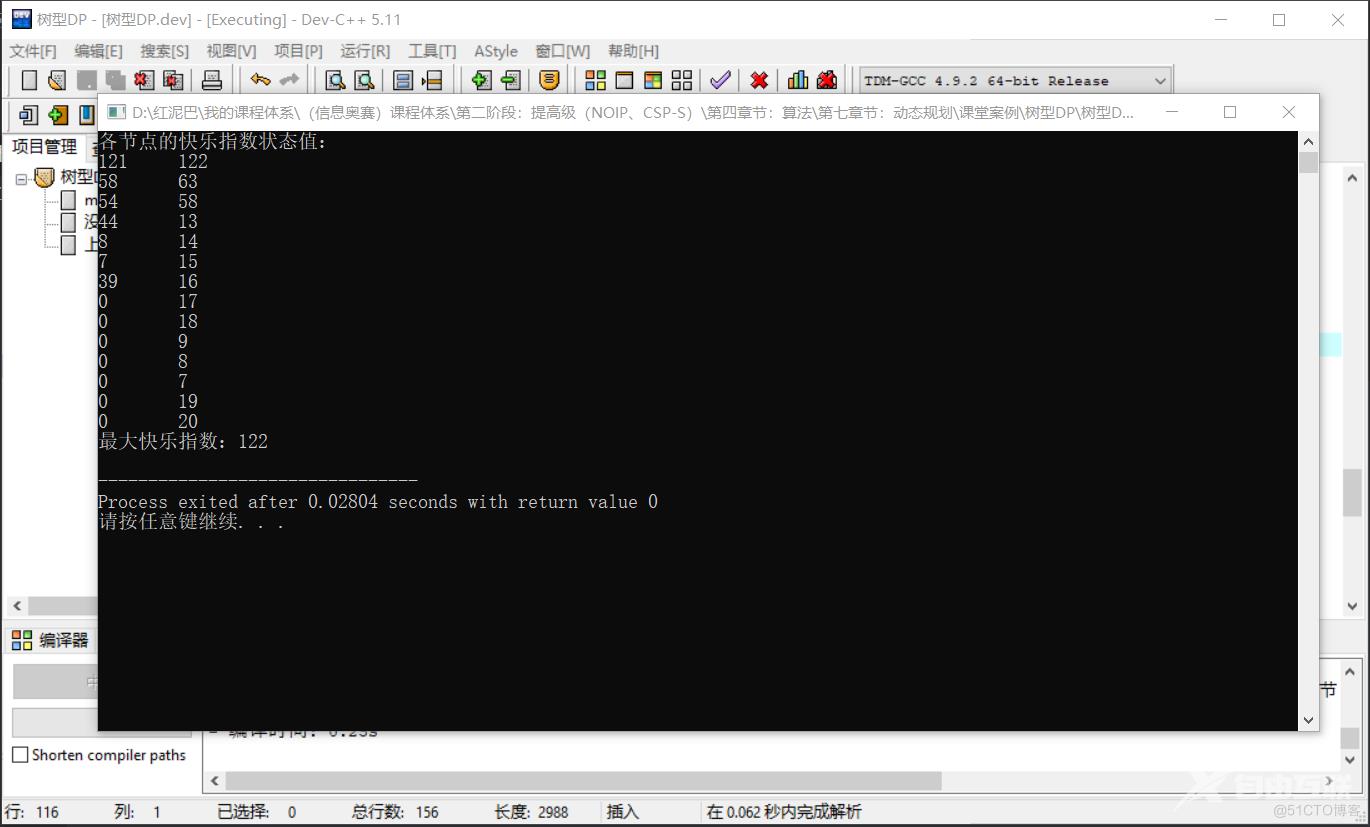
2.2 没有上司的舞会的升级版
问题描述:
在上述没有上司的舞会的案例中,添加如下的限制。由于场地有大小限制,场地最多只能容纳 m(1≤m≤n) 个人。请求出快乐值最大是多少。
问题分析:
相比较上一个问题,对于每一个员工,都有去或不去的选择。上文使用二维数组存储当编号为 i的员工去或不去时的快乐指数状态值。此问题多了一个人数限制,对于每一个员工(节点)而言,除了考虑去或不去,还需要考虑他以及他的下属一共有多少人参加舞会。
所以,需要添加一个新的维度,团队中参加舞会的人数。如下图所示:
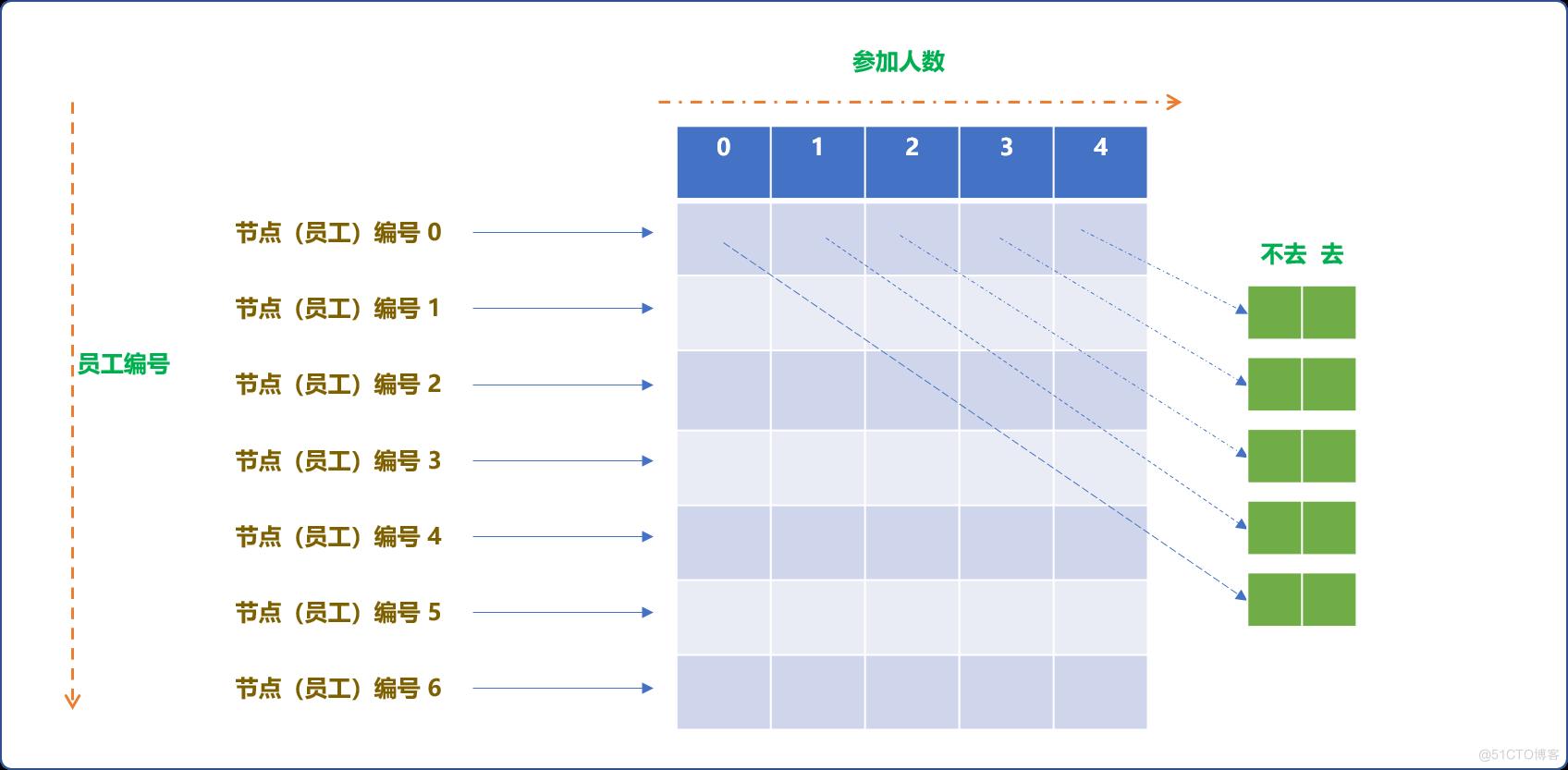
如果员工编号使用 i表示,人数使用 k,去或不去使用 j表示,则状态数组happys[1][1][0]表示编号为1的员工不去时,且人数限制为 1的最优快乐指数。
知道状态信息后,需要找出状态转移方程式。
//编号为 i 的员工不去。p 取值范围为 0~k
f[i][k][0] = max(f[i][k][0], f[i][k - l][0] + max(f[子节点编号][p][0], f[子节点编号][p][1]));
//编号为 i 的员工去。
f[i][k][1] = max(f[i][k][1], f[i][k - l][1] + f[子节点编号][p][0]);
编号实现:
在上面代码基础之上,修改 2 处位置,一个是状态数组。一个是深度搜索算法。
//省略……
/*
*节点类 省略……
*/
/*
*树(舞会)类
*/
class Dance {
private:
//省略……
//三维状态数组,行号为员工编号
int happys[100][100][2];
public:
//省略……
/*
* 深度搜索实现
* 树型动态规划
* empId: 当前员工编号
* count: 限制人数
*/
void dfs(int empId,int count) {
//对于当前节点:去但是人数限制为 0
happys[empId][0][1] = 0;
for (int k =count; k; --k)
//对于当前节点:去,人数限制不同的时候的状态值
happys[empId][k][1] = happys[empId][k - 1][1] +this->emps[empId].happy;
//查询子节点信息
for(int subEmpId: this->relationship[empId]) {
//基于子节点深度搜索
dfs(subEmpId,count) ;
for (int k = count; k >= 0; --k)
for (int l = 0; l <= k; l++) {
//不去
happys[empId][k][0] = max(happys[empId][k][0], happys[empId][k - l][0] + max(happys[subEmpId][l][0], happys[subEmpId][l][1]));
happys[empId][k][1] = max(happys[empId][k][1], happys[empId][k - l][1] + happys[subEmpId][l][0]);
}
}
}
//输出最大快乐指数
void maxHappy(int count) {
cout<<"最大快乐指数:"<< max(this->happys[0][count][0],this->happys[0][count][1] )<<endl;
}
};
int main() {
Dance dance(14);
//省略……
dance.dfs(root,3);
dance.maxHappy(3);
return 0;
}
输出结果:
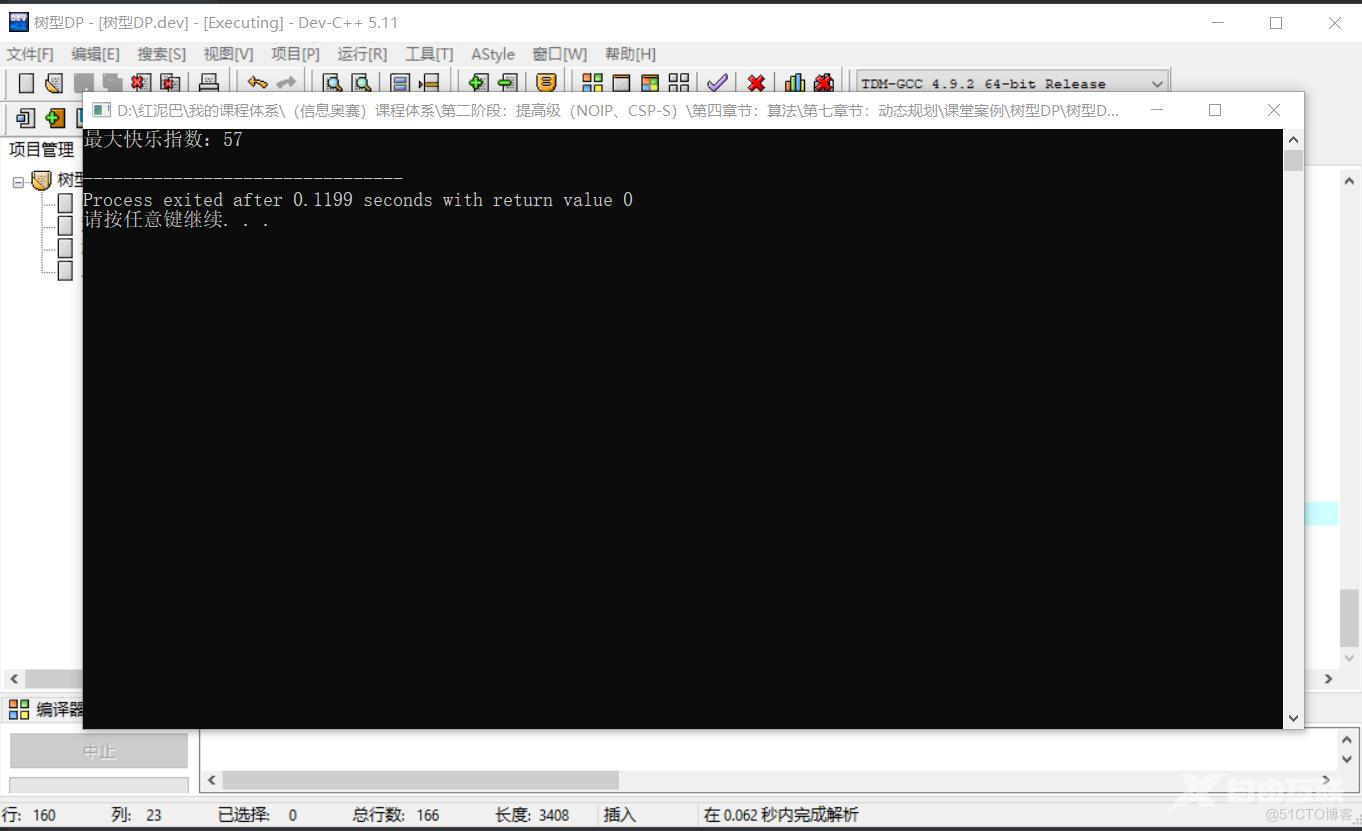
2.3 城堡守卫者
问题描述:
一座城堡的所有的道路形成一个n个节点的树,如果在一个节点上放上一个士兵,那么和这个节点相连的边就会被看守住,问把所有边看守住最少需要放多少士兵。
问题分析:
此题目和上述没有上司的舞会的题意差不多。同样可以使用二维数组存储第一个节点的状态值。这里状态值指以当前节点为根节点时子树所需要的最小士兵值。
soldiers[100][2];
//soldiers[1][0] 表示编号为 1 的节点处不放置士兵时树的士兵总数
//soldiers[1][1] 表示编号为 1 的节点处放置士兵时树的士兵总数
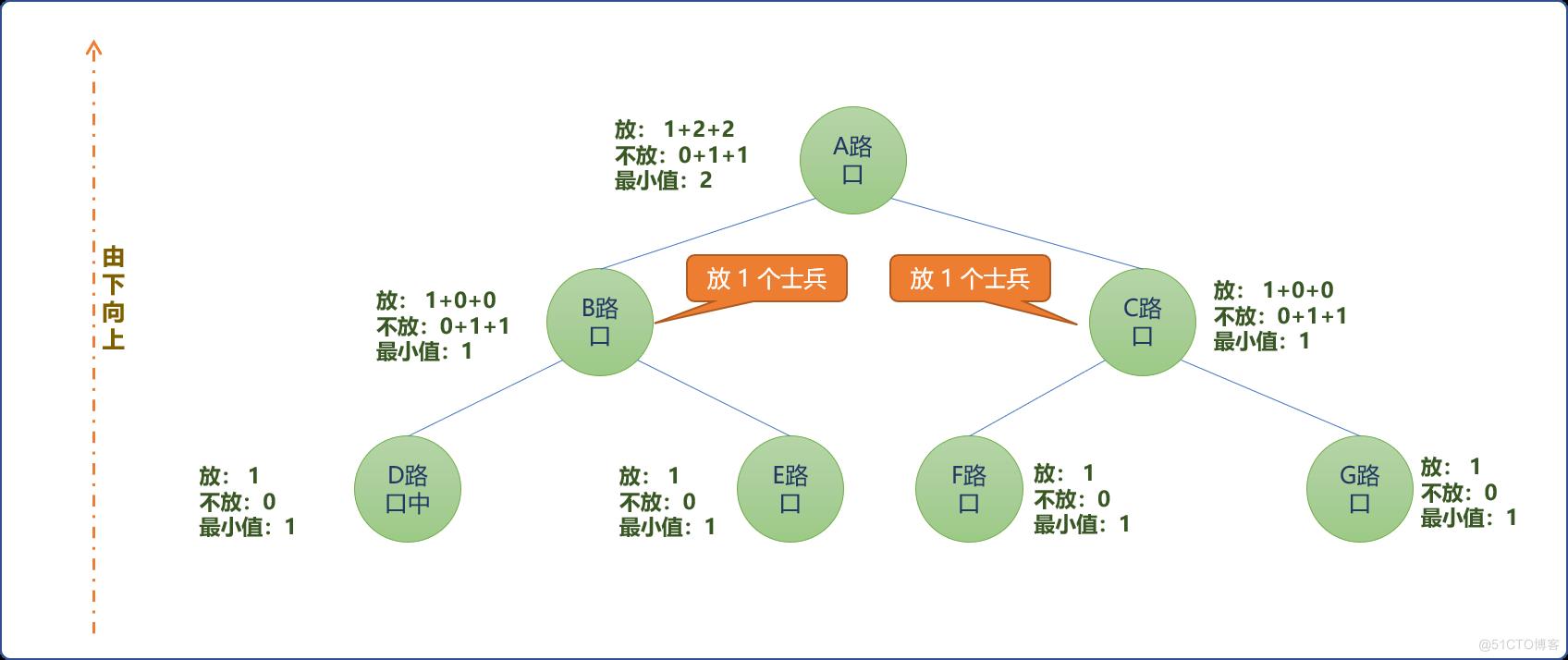
如下图,当只有一个节点时的节点状态值:
- 对于此节点而言,有
2种状态,放一个士兵或不放一个士兵。当只有一个节点时,理论上可以放或不放一个士兵,但从现实而言,至少需要放一个士兵。意味着min(soldiers[0][1,soldiers[0][0])>0(最小值不能为零),如果结果为0至少需要放1个士兵。

- 节点有子节点时。则状态值如下图所示。
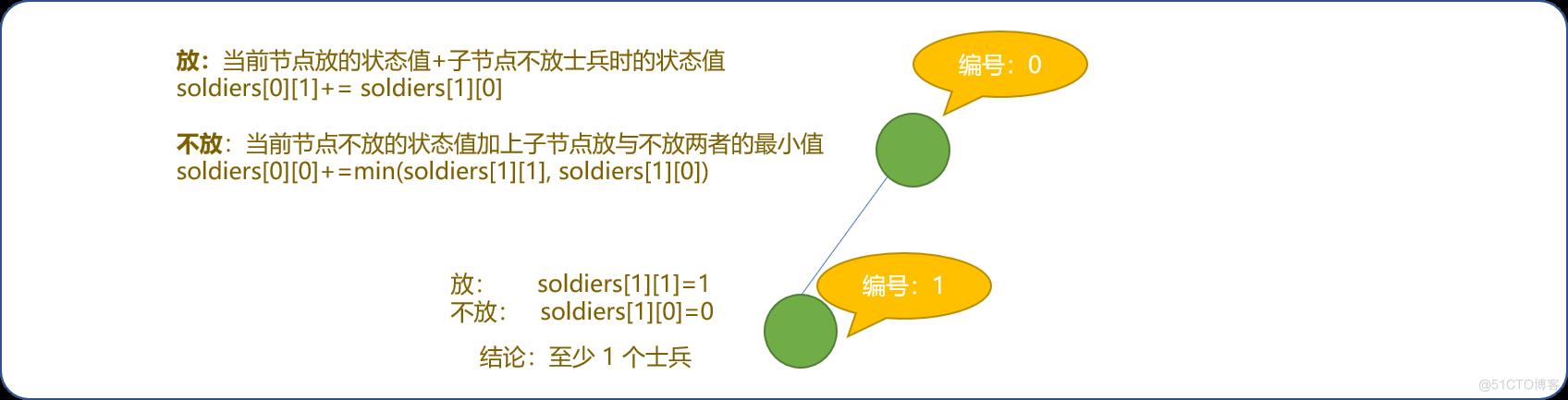
- 如下图所示,根据树型动态规划思想,到根结点时,最优状态值为
2, 只需要在B路口和C路口各放一个士兵,便能守住整棵树。
编码实现:
代码与上面案例的代码很类似,为了做些区分。此案例中,节点之间的关系使用邻接表的方式。直接上所有代码,细节处自行了解。
#include <iostream>
#include <vector>
using namespace std;
/*
*节点类
*/
struct Crossing {
//路口编号
int cid;
//路口名
string cname;
//使用邻接表存储与之相信的节点的编号
vector<int> neighbours;
Crossing() {}
Crossing(int cid,string cname) {
this->cid=cid;
this->cname=cname;
}
};
/*
* 城堡树
*/
class City {
private:
//所有路口
Crossing crossings[100];
//路口数量
int crossingCount;
//数量
int count;
//编号
int num;
//二维状态数组,行号为路口编号
int soldiers[100][2];
public:
City() {}
City(int count) {
this->num=0;
//路口数量
this->crossingCount=count;
}
/*
* 添加路口
*/
int addCrossing(string cname) {
//新路口
Crossing crossing(this->num,cname);
//添加
this->crossings[this->num]=crossing;
return this->num++;;
}
/*
*添加路口间父子关系
*/
void addRelation(int from,int to) {
//邻接表
this->crossings[from].neighbours.push_back(to);
}
/*
*规定编号为 0 的员工为根节点
*/
int getRoot() {
return 0;
}
/*
* 深度搜索实现
* 树型动态规划
*/
void dfs(int cid) {
//不放
soldiers[cid][0]=0;
//放
soldiers[cid][1]=1;
//深度搜索子节点
for(int i=0; i< this->crossings[cid].neighbours.size(); i++ ) {
int subId= this->crossings[cid].neighbours[i];
//基于子节点深度搜索
dfs(subId) ;
//放
soldiers[cid][1]+= soldiers[subId][0];
//不放
soldiers[cid][0]+= min(soldiers[subId][1],soldiers[subId][0]) ==0?1:min(soldiers[subId][1],soldiers[subId][0]);
}
}
/*
*输出
*/
void outInfo() {
cout<<"各路口的士兵数:"<<endl;
for(int i=0; i<this->num; i++) {
for(int j=0; j<2; j++) {
cout<<this->soldiers[i][j]<<"\t";
}
cout<<endl;
}
cout<<"最小士兵人数:"<< min(this->soldiers[0][0],this->soldiers[0][1] )<<endl;
}
};
//测试
int main() {
City city(7);
int root= city.addCrossing("A路口") ; //0
int bRoad= city.addCrossing("B路口") ;
city.addRelation(root,bRoad);
int cRoad= city.addCrossing("C路口") ;
city.addRelation(root,cRoad);
int dRoad= city.addCrossing("D路口") ;
city.addRelation(bRoad,dRoad);
int eRoad= city.addCrossing("E路口") ;
city.addRelation(bRoad,eRoad);
int fRoad= city.addCrossing("F路口") ;
city.addRelation(cRoad,fRoad);
int gRoad= city.addCrossing("G路口") ;
city.addRelation(cRoad,gRoad);
city.dfs(root);
city.outInfo();
return 0;
}
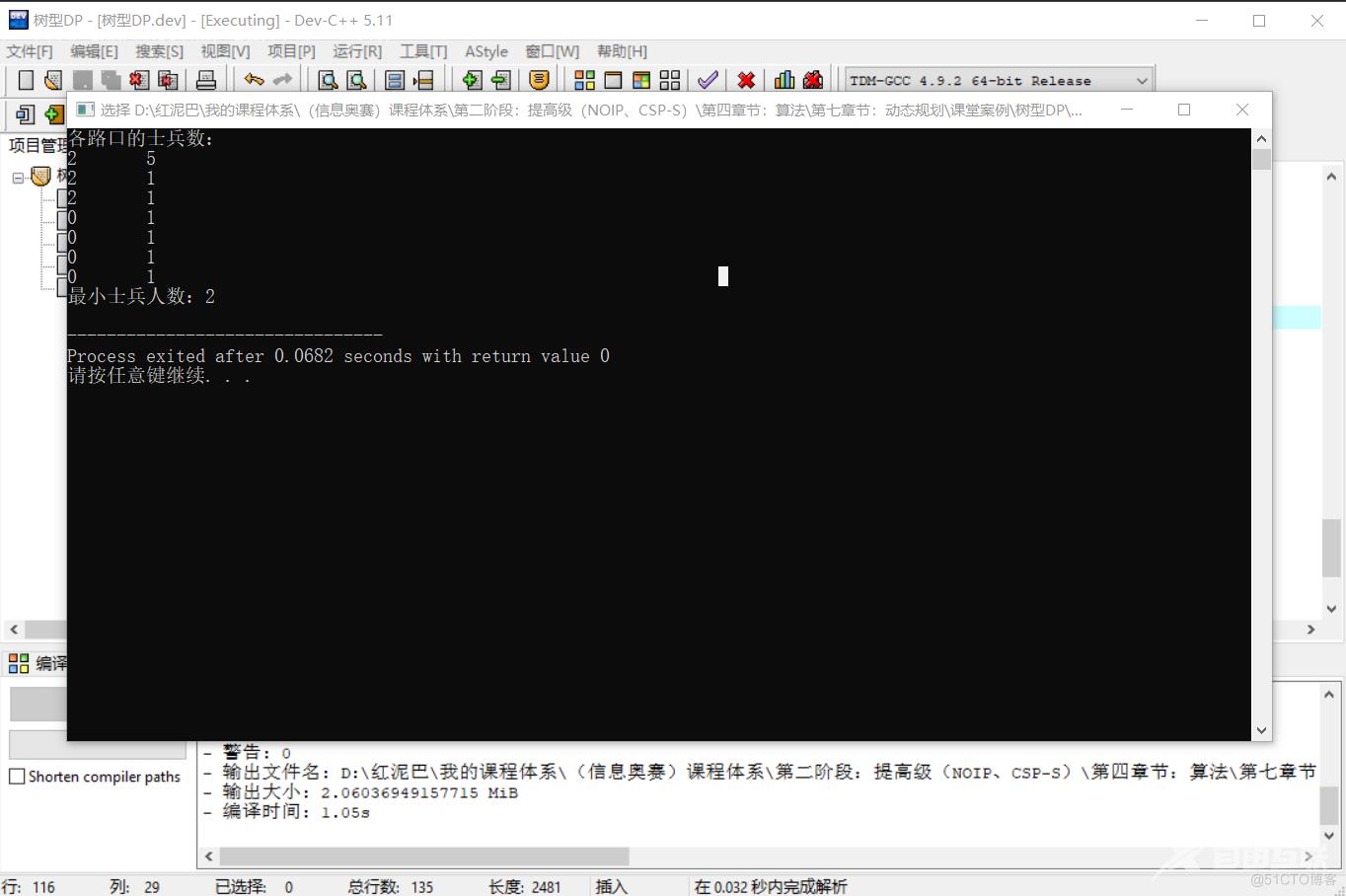
输出结果:
3. 总结
本文讲解树型动态规划,是动态规划思想用于基于树结构的问题求解方案。
动态规划是一个很重要的算法思想,入门较易,但,因其可适用的场景较多,导致其变化性很大。虽如此,但万变不离其宗,找到子问题的状态值以及状态转换表达式,问题也将迎刃而解。
