【内附源码和文档】人工智能实验盲目搜索

人工智能实验盲目搜索

一、 无信息搜索（盲目搜索）

1.算法原理
1.1 搜索问题的形式化定义
解决搜索问题时，首先需要对搜索问题进行形式化表述。搜索问题从以下几个方面表述：

状态空间：对问题的形式化，表示需要进行搜索的空间
动作：对真正动作的形式化，表示从一个状态到达另一个状态
初始状态：表示当前的状态
目标：表示需要达到的目标的状态
启发方法：用于指挥搜索的前进方向的方法
问题的解：一个从初始状态到达目标状态的动作序列
搜索问题可以用状态空间树表示，每个节点对应着状态空间中的一种状态。节点的父节点表示产生该状态的上一个状态，父节点生成子节点时需要记录生成节点所采取的行动与代价。

搜索算法的性能需要考虑一个方面：

完备性：当问题有解时是否一定能找到解
最优性：搜索策略是否一定能找到最优解
时间复杂度：找到解所需要的时间，又称为搜索代价
空间复杂度：执行搜索过程中需要多少内存空间
1.2 无信息搜索的具体算法
1.2.1 宽度优先搜索
宽度优先搜索用一个先进先出的队列实现，节点的拓展顺序与目标节点的位置无关。从状态空间树上看，宽度优先搜索的拓展顺序是按树的层次顺序来进行的。这样一来，短的路径会在任何比它长的路径之前被遍历，因此宽度优先搜索具有完备性和最优性。

定义为问题中一个状态最大的后继状态个数，为最短解的动作个数，则有：

时间复杂度：
空间复杂度：
1.2.2 深度优先搜索
把当前要扩展的状态的后继状态放在边界的最前面，边界上总是扩展最深的那个节点。在状态空间无限或在状态空间有限，但是存在无限的路径（例如存在回路） 的情况下不具有完备性。在状态空间有限，且对重复路径进行剪枝的情况下才有。不具有最优性。

定义m是遍历过程中最长路径的长度，则有：

时间复杂度：

空间复杂度：

1.2.3 一致代价搜索
边界中，按路径的成本升序排列，总是扩展成本最低的那条路径。当每种动作的成本是一样的时候，和宽度优先是一样的。假设每个动作的成本都大于某个大于0的常量，所有成本较低的路径都会在成本高的路径之前被扩展。给定成本，该成本的路径数量是有限的；成本小于最优路径的路径数量是有限的，最终，我们可以找到最短的路径，因此具备完备性和最优性。

对于一致代价搜索，当最优解的成本为C* ，上述最低代价为 ，则有：

时间复杂度：
空间复杂度：
1.2.4 深度受限搜索
深度受限搜索是深度优先搜索，但是预先限制了搜索的深度L，因此无限长度的路径不会导致深度优先搜索无法停止的问题。 但只有当解路径的长度 ≤ L 时，才能找到解，故不具有完备性和最优性。

时间复杂度：
空间复杂度：
1.2.5 迭代加深搜索
一开始设置深度限制为L = 0，迭代地增加深度限制，对于每个深度限制都进行深度受限搜索 。如果找到解，或者深度受限搜索没有节点可以扩展的时候可以停止当前迭代，并提高深度限制L 。如果没有节点可以被剪掉（深度限制不能再提高）仍然 没有找到解，那么说明已经搜索所有路径，因此这个搜索不存在解。具有完备性，且在每个动作的成本一致时具有最优性。

1.2.6 双向搜索
同时进行从初始状态向前的搜索和从目标节点向后搜索，在两个搜索在中间相遇时停止搜索。假设两个搜索都使用宽度优先搜索，则具有完备性，在每条边/每个动作的成本一致的情况下具有最优性。

2. 流程图和伪代码

为了便于比较算法差异，我实现了宽度优先搜索和双向搜索两种算法。

2.1 宽度优先搜索

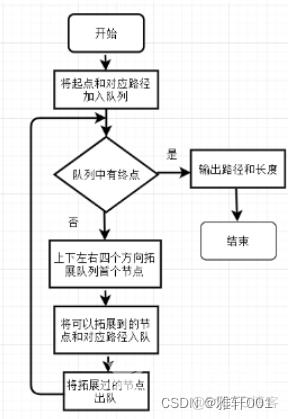
判断队列是否有终点和输出路径较为简单，下面只讨论算法终点部分。

每次取出队列首个节点，记其坐标为(x,y)，向上下左右四个方向拓展新的四个节点。拓展节点的方式如下：

input: queue
/* 输入当前节点队列 */
output: queue
/* 输出更新后的队列 */
def expand(queue)
	(x,y) = queue.front();	/* 取出队首的节点 */
	/* 向上下左右四个方向拓展新的节点 */
	expand_node(x+1,y);
	expand_node(x-1,y);
	expand_node(x,y+1);
	expand_node(x,y-1);
	/* 将当前节点出队 */
	queue.pop();

判断具体的节点是否要加入队列时，判断节点位置是否是通路’0’或终点’E’即可。考虑到迷宫四周一圈都是墙壁’1’，所以不需要考虑出界的问题。

input: queue, x, y
/* 输入当前节点队列，要加入的新节点的坐标 */
output: queue
/* 输出更新后的队列 */
def expand_node(queue, x, y)
	if (x,y) 处为通路或终点
	then
		queue.push((x,y))
		将(x,y)处变为墙壁

完整的源码和详细的文档，上传到了 【WRITE-BUG数字空间】，需要的请自取：
https://www.writebug.com/code/0c802727-c792-11ed-ac02-6479f0e5e323/#