【数据结构】栈

栈的定义和特点

栈是一个特殊的线性表，是限定仅在一端（通常是表尾）进行插入和删除操作的线性表。

又称为后进先出的线性表，简称LIFO结构。

栈是仅在表尾进行插入、删除操作的线性表。

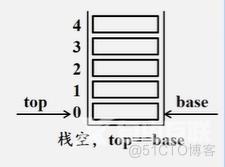
表尾称为栈顶top，表头称为栈底base

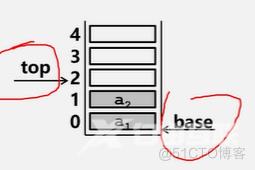
插入元素到栈顶（即表尾）的操作，称为入栈。

从栈顶（即表尾）删除最后一个元素的操作，称为出栈

“入”=压入push（x)  "出"=弹出pop（y)

重要结论

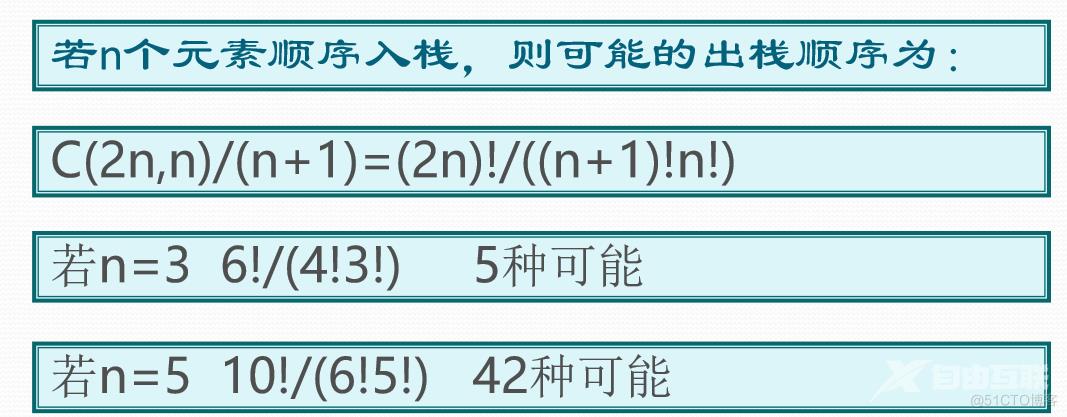
栈的抽象数据类型的类型定义

ADT Stack {

数据对象：D＝{ ai | ai ∈ElemSet, i=1,2,...,n, n≥0 } 数据关系：R1＝{ <ai-1, ai >| ai-1, ai∈D, i=2,...,n } 约定an 端为栈顶，a1 端为栈底。

基本操作： 

InitStack(&S)     操作结果：构造一个空栈S

DestroyStack(&S)     初始条件：栈 S 已存在。 操作结果：栈 S 被销毁。 

ClearStack(&S)     初始条件：栈 S 已存在。     操作结果：将 S 清为空栈。

StackEmpty(s)     初始条件：栈 S 已存在。       操作结果：若栈 S 为空栈，返回 TRUE，否则返回 FALSE。

StackLength(S)     初始条件：栈 S 已存在。      操作结果：返回 S 的元素个数，即栈的长度。 

GetTop(S, &e)     初始条件：栈 S 已存在且非空。操作结果：用 e 返回 S 的栈顶元素。

Push(&S, e)     初始条件：栈 S 已存在。              操作结果：插入元素 e 为新的栈顶元素。

Pop(&S, &e)     初始条件：栈 S 已存在且非空。    操作结果：删除栈顶元素，并用 e 返回其值。

StackTravers(S, visit())     初始条件：栈 S 已存在且非空。     操作结果：从栈底开始遍历栈。 } ADT Stack 

栈的表示和实现

由于栈本身就是线性表，于是栈也有顺序存储和链式存储两种实现方式。

栈的顺序存储——顺序栈

栈的链式存储——链栈

顺序栈的表示和实现

存储方式：同一般线性表的顺序存储结构完全相同

利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素。栈底一般在低地址端。

附设top指针，指示栈顶元素在顺序栈中的位置。

另设base指针，指示栈底元素在顺序栈中的位置。

但是，为了方便操作，通常top指示真正的栈顶元素之上的下标地址。

另外，用stacksize表示栈可使用的最大容量。

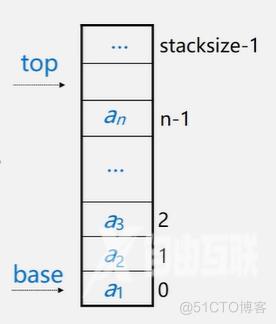
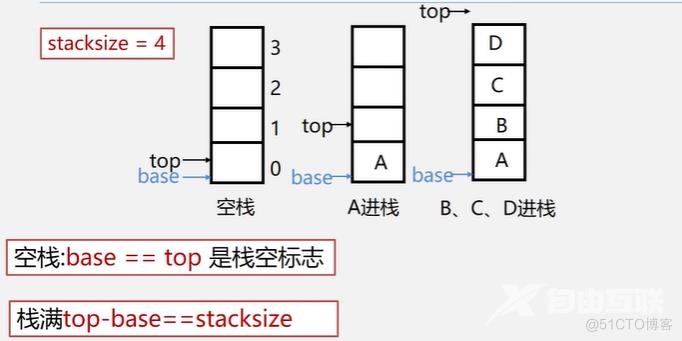
栈满时的处理方法：

1.报错，返回操作系统

2.分配更大的空间，作为栈的存储空间，将原栈的内容移入新栈。

使用数组作为顺序栈存储方式的特点：

简单、方便、但易产生溢出，数组大小固定

上溢（OVERFLOW）:栈已经满，又要压入元素

下溢（UNDERFLOW）：栈已经空，还要弹出元素

注：上溢是一种错误，使问题的处理无法进行；而下溢一般认为是一种结束条件，即问题处理结束。

#define MAXSIZE 1000
typedef struct
{
ElemType *base;//栈底指针
ElemType *top;//栈顶指针
int stacksize;//栈可用最大容量
}SqStack;

顺序栈的初始化

Status InitStack( SqStack &S) 
{
s.base=(SElemType*)malloc(MAXSIZE*sizeof(SElemType));     
if(!s.base) exit(OVERFLOW);     
s.top=s.base;    
s.stacksize=MAXSIZE;     
return OK;
}

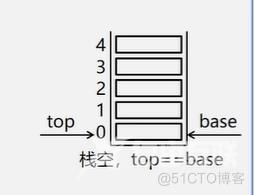
顺序栈判断栈是否为空

Status StackEmpty(SqStack S)
{
if(S.top==S.base)
return TRUE;
else
return FALSE;
}

求顺序栈的长度

int StackLength(SqStack S)
{
return S.top-S.base;
}

清空顺序栈

Status ClearStack(SqStack S)
{
if(S.base)
S.top=S.base;
return OK;
}

销毁顺序栈

Status DestroyStack(SqStack &S)
{
  if(S.base)
  {
    delete S.base;
    S.stacksize=0;
    S.base=S.top=NULL;
  }
  return OK;
}

取栈顶元素

Status GetTop(SqStack s,SElemType &e)
{
  if(s.top==s.base)
    return ERROR;
  e=*(s.top-1);
  return OK;
}

⭐顺序栈的入栈

1.判断是否栈满，若满则出错（上溢）

2.元素e压入栈顶

3.栈顶指针加1

Status  Push(SqStack  &s , SElemType e){
    if(s.top-s.base>=s.stacksize)  {
        s.base=(SElemType*) realloc (s->base,(s.stacksize+STACKINCREMENT)*sizeof(SElemType));
        if(!s.base) exit(OVERFLOW);
        s.top=s.base+s.stacksize;
        s.stacksize+=STACKINCREMENT;
    }
    *s.top++ = e;//*S.top=e; S.top++;
    return OK;
}

⭐顺序栈的出栈

1.判断是否栈空，若空则出错（下溢）

2.获取栈顶元素e

3.栈顶指针减1

Status  Pop(SqStack  &s,SElemType &e)
{     
  if(s.top==s.base) //等价if(StackEmpty(S)) 
    	return ERROR; 
 e = *--s.top ;//--S.top; e=*S.top   
 return OK;
}

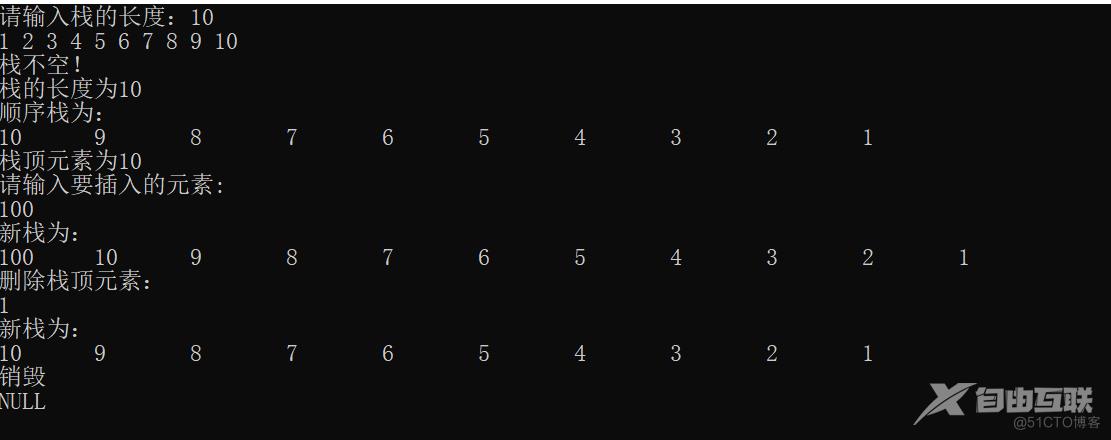
顺序栈代码实现

#include<stdio.h>
#include<stdlib.h>
#define STACK_INIT_SIZE 100
#define STACKINCREMENT 10
#define OK 1
#define OVERFLOW -2
#define ERROR 0
typedef int SElemType;
typedef int Status;

typedef struct{
   SElemType  *base;
   SElemType  *top;
   int stacksize;
}SqStack;

Status InitStack(SqStack *s)
{
  s->base=(SElemType*)malloc(STACK_INIT_SIZE*sizeof(SElemType));
  if(!s->base)
   exit(OVERFLOW);
  s->top=s->base;
  s->stacksize=STACK_INIT_SIZE;
  return OK;
}


Status GetTop(SqStack s,SElemType* e)
{
  if(s.top==s.base)
   return ERROR;
  *e=*(s.top-1);
  return OK;
}

Status Push(SqStack *s,SElemType e)
{
  if(s->top-s->base>=s->stacksize)
  {
    s->base=(SElemType*) realloc (s->base,(s->stacksize+STACKINCREMENT)*sizeof(SElemType));
    if(!s->base) exit(OVERFLOW);
    s->top=s->base+s->stacksize;
    s->stacksize+=STACKINCREMENT;
  }
  *s->top++=e;
  return OK;
}

Status Pop(SqStack *s,SElemType *e)
{
  if(s->top==s->base)
   return ERROR;
  *e=* -- s->top;
  return OK;
}

Status StackEmpty(SqStack s)
{
  return s.top==s.base;
}

Status StackLength(SqStack *S)
{
	if(S->top==S->base)
		return 0;
	else
	return (Status)(S->top-S->base);
}
Status DestroyStack(SqStack *S)
{
	free(S->base);
	S->base=S->top=NULL;
	S->stacksize=0;
	return OK;
}
Status ClearStack(SqStack S)
{
	if(S.base)
	S.top=S.base;
	return OK;
}
Status StackTraverse(SqStack *S)
{
	SElemType *p;
	if(S->top==S->base)
	{
		printf("NULL\n");
		return 0;
	}
	p=S->top;
	while(p>S->base)
	{
		p--;
		printf("%d\t",*p);
	}
	printf("\n");
	return OK;
}
int main()
{
	SqStack S;
	InitStack(&S);
	SElemType e;
	int x,i;
	printf("请输入栈的长度：");
	scanf("%d",&x);
	for(i=1;i<=x;i++)
	{
		scanf("%d",&e);
		Push(&S,e);
	}
	if(StackEmpty(S))
	{
		printf("栈空！\n");
	}
	else
	{
		printf("栈不空！\n");
	}
	printf("栈的长度为%d\n",StackLength(&S));
	printf("顺序栈为：\n");
	StackTraverse(&S);
	GetTop(S,&e);
	printf("栈顶元素为%d\n",e);
	printf("请输入要插入的元素:\n");
	scanf("%d",&e);
	Push(&S,e);
	printf("新栈为：\n");
	StackTraverse(&S);
	printf("删除栈顶元素：\n");
	e=Pop(&S,&e);
	printf("%d\n",e);
	printf("新栈为：\n");
	StackTraverse(&S);
	printf("销毁\n");
	DestroyStack(&S);
	StackTraverse(&S);
	return 0;
}

链栈的表示和实现

链栈是运算受限的单链表，只能链表头部进行操作

链栈可以有头结点，也可以不设头结点。

带有头结点时，空栈时head->next=NULL 不带头结点，空栈时head=NULL 链栈的栈顶元素以头指针唯一标识，即链栈的头指针即为栈顶指针。 链栈不设置栈底指针。 

typedef struct StackNode
{
  ElemType data;
  struct StackNode *next;
}StackNode,*LinkStack;
LinkStack S;

链表的头指针就是栈顶

不需要头结点

基本不存在栈满的情况

空栈相当于头指针指向空，链栈的空其实就是top=NULL的时候

插入和删除仅在栈顶处执行

链栈的结构代码

typedef struct SNode
{
	SElemType  data;
	struct SNode  *next;
}SNode, *LinkStack;

链栈初始化

void InitStack(LinkStack &S)
{
  S=NULL;
  return OK;
}

判断链栈是否为空

Status StackEmpty(LinkStack S)
{
  if(S==NULL)
    	return TRUE;
  else
  		return FALSE;
}

链栈的入栈

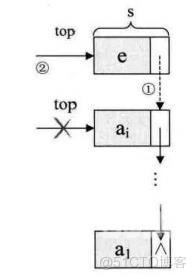
Status Push(LinkStack &S,ElemType e)
{
  LinkStack s;
  s=(LinkStack)malloc(sizeof(Node));
  s->data=e;//将新结点数据域置为e
  s->next=S->top;//把当前的栈顶元素赋给新结点的直接后继，如图中①
  S->top=s;//将新的结点e赋值给栈顶指针，如图中②
  return OK;
}

链栈的出栈

至于链栈的出栈操作，也是简单的三句操作。假设变量p用来存储要删除的栈顶结点，将栈顶指针下移一位，最后释放p即可。

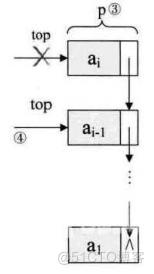
//若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK，否则返回ERROR；
Status Pop(LinkStack *S,ElemType *e)
{
  LinkStack p;
  if(StackEmpty(*S))
    return ERROR;
  *e=S->top->data;
  p=S->top;//将栈顶结点赋值给p，如图中③
  S->top=S->top->next;//使得栈顶指针下移一位，指向后一结点，如图中④
  free(p);
  return OK;
}

链栈的出栈和入栈时间复杂度皆为O（1）

取栈顶元素

ElemType GetTop(LinkStack S)
{
  if(S!=NULL)
    return S->data;
}

对比下顺序栈与链栈，它们在时间复杂度上是一样的，均为 O(1) 。对于空间性能，顺序栈需要事先确定一个固定的长度，可能会存在内存空间浪费的问题，但它的 优势是存取时定位很方便，而链栈则要求每个元素都有指针域，这同时也增加了一些 内存开销，但对于栈的长度无限制。所以它们的区别和线性表中讨论的一样， 如果栈的使用过程中元素变化不可预料，有时很小，有时非常大，那么最好是用链栈，反之，如果它的变化在可控范围内，建议使用顺序栈会更好一些。

链栈代码实现

#include<stdio.h>
#include<stdlib.h>
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status;
typedef int SElemType;
//定义链栈
typedef struct SNode
{
	SElemType data;
	struct SNode *next;
}SNode,*SNodeptr;
typedef struct LinkStack
{
	SNodeptr top;
	int count;
}LinkStack;
int InitStack(LinkStack *S)
{
	S->top=(SNodeptr)malloc(sizeof(SNode));
	if(S->top=NULL)
		return 0;
	else
	{
		S->top=NULL;
		S->count=0;
		return 1;
	}
	return OK;
}
Status StackEmpty(LinkStack S)
{
	if(S.top=NULL)
		return TRUE;
	else
		return FALSE;
}
Status Push(LinkStack *S,SElemType e)
{
  SNodeptr s;
  s=(SNodeptr)malloc(sizeof(SNode));
  s->data=e;//将新结点数据域置为e
  s->next=S->top;//把当前的栈顶元素赋给新结点的直接后继
  S->top=s;//将新的结点e赋值给栈顶指针
  return OK;
}
//若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK，否则返回ERROR；
Status Pop(LinkStack *S,SElemType *e)
{
  SNodeptr p;
  if(StackEmpty(*S))
    return ERROR;
  *e=S->top->data;
  p=S->top;//将栈顶结点赋值给p
  S->top=S->top->next;//使得栈顶指针下移一位，指向后一结点
  free(p);
  return OK;
}
SElemType GetTop(LinkStack S)
{
	SNodeptr p;
	p=S.top;
	if(StackEmpty(S))
		return ERROR;
	else
		return p->data;
}
Status StackLength(LinkStack S)
{
	int n=0;
	SNodeptr p;
	p=S.top;
	while(p)
	{
		n++;
		p=p->next;
	}
	return n;
}
Status ClearStack(LinkStack *S)
{
	SNodeptr p,q;
	p=S->top;
	while(p)
	{
		q=p;
		p=p->next;
		free(q);
	}
	S->count=0;
	return OK;
}
Status DestroyStack(LinkStack *S)
{
	SNodeptr p=S->top,q;
	while(p)
	{
		q=p->next;
		free(p);
		p=q;
	}
	return OK;
}
void Print(LinkStack S)
{
	SNodeptr p=S.top;
	while(p)
	{
		printf("%d\t",p->data);
		p=p->next;
	} 
}
int main()
{
	LinkStack S;
	InitStack(&S);
	int x,i;
	SElemType e;
	printf("请输入栈的长度：");
	scanf("%d",&x);
	for(i=1;i<=x;i++)
	{
		scanf("%d",&e);
		Push(&S,e);
	}
	Print(S);
	e=StackLength(S);
	printf("\n该链栈的长度为%d\n",e);
	e=GetTop(S);
	printf("\n该链栈的栈顶元素为%d\n",e);
	printf("\n删除栈顶元素\n");
	Pop(&S,&e);
	printf("删除后的栈为：\n");
	Print(S);
	return 0;
}