对于单链表有环问题,上一期,我们已经详细讲解了!!而快慢指针功不可没!!
对于本期 我们再次回顾,链表有环问题时,不难心中存在一个疑问,一定能追得上吗? 会不会错过??
那么为什么??为何能追上,什么情况下会追不上!!这就是我们今天讨论的重点!!
假设单链表有环,快指针每次走两步,而慢指针每次走一步!!那么,快慢指针总会全都入环,并且一定是快指针先入环。当慢指针入环的时候,两个指针相差的距离,最坏的情况是环的长度 - 1
而每次,快指针总是比慢指针多走一步!!这样会之间的距离就会缩小一步!!并且不会出现套圈的现象!!而且在慢指针走完一圈之内快指针一定会同慢指针相遇
由于方便理解与论述,请看下面的图示 :>

以上仅仅是一种情况,那么问题又来了!!如果,每一次 slow 走一步,而 fast 会走 X (X >= 3) 步呢??
会相遇吗?又是否会错过??
还是同样,为方便理解以及更加形象化,请看下面的图解 :>
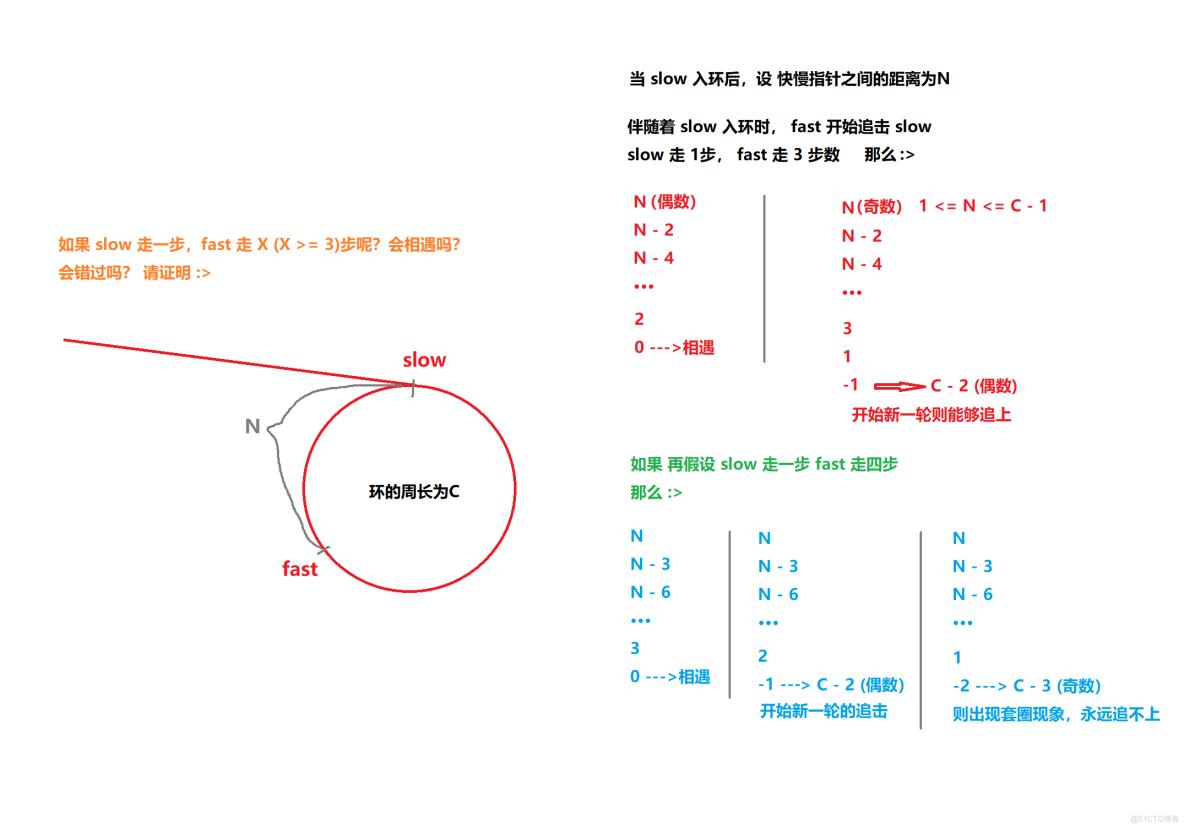
由以上过程的讨论,我们不难看出,对于 N 的奇偶性需额外注意的!!
另外步数相差 偶数倍 与 还是相差 奇数倍 也还是有区分的!!
下面,我们再证明一道 ::>
让一个指针从链表的起始位置开始遍历链表,同时让一个指针从判环时相遇的位置开始绕环运行,两个指针都是每次均走一步,最终会在第一次入环的位置相遇。请证明!
本道证明题,是不是特别有熟悉感! 其实,它是上一期最后一道题的拓展!!
原题如下 ::>
给定一个链表的头结点 head,返回链表开始入环的第一个结点。如果链表无环则返回 NULL。
而代码实现则如下 :>

为了更加容易理解证明过程,还是图像形象化比较好,如下所示 :>
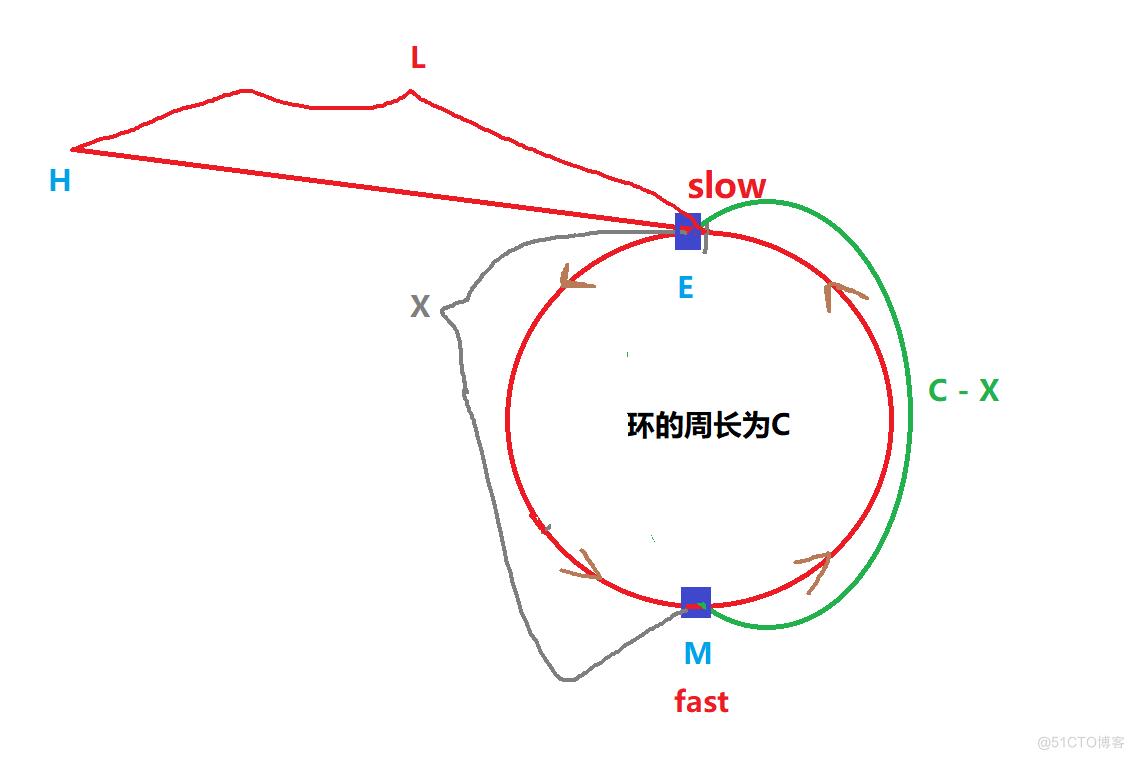
如图所示,假设,H为起始点,E为入环点,
M为相遇点,也是 fast开始追击 slow 的起始点(或者说,slow 刚刚入环的时候,fast 所在的位置)
设 长度ME 为 L ,EM之间的距离为X , ME 间距为 C - X
判环过程中,快指针与慢指针相遇时,有 ::>
slow = L + X
fast = L + X + nC ,(n ,1, 2, 3, 4, 5, 6 ···)
现请注意 :>
1.慢指针入环时,快指针已经在环中运动了n圈。n 至少为 1
因为 :slow 入环时, fast 位于 M 点处,之后追击 slow 又在M点处两者相遇
2.slow 入环,fast 会在slow 完成一圈之内,追上 slow
因为:fast 与 slow 之间的最大距离为环的长度 C, 由于fast 比 slow 要快走一步,每一次会使得之间的距离缩短一个单位,因此 slow 入环之后,fast 在一圈之内一定会追上 slow
由于满足 fast 的行进速度是slow的两倍(噢!!这让我想起了高中物理的速度是矢量,是有方向的,前面的表述口误了,哈哈
