AVL树
AVL树的定义和性质
在输入值不够随机,或者经过某些插入或删除操作时,二叉搜索树会失去平衡,降低搜索效率,极端情况下,当插入数据接近有序时,二叉搜索树会退化为链表,导致搜索效率近似下降为O(N)。为了尽量保证二叉搜索树的平衡,两位俄罗斯的数学家 G.M.Adelson-Velskii 和 E.M.Landis 在1962年发明了AVL树。
AVL树是一种平衡搜索二叉树,其具有以下性质:
- 它的左右子树都是AVL树;
- 它的左右子树的高度差的绝对值不超过 1.
AVL树是一个加上了平衡条件的二叉搜索树,其平衡条件的建立是为了确保整棵树的深度为log(N),以使搜索效率近似保持在log(N)。直观上的平衡其实是每个节点的左右子树的高度相等,但是这种条件十分苛刻,很难插入新元素且保持这样的平衡,于是AVL树退而求其次,使左右子树的高度最多相差为 1,保证这个较弱的条件,仍然能够保证对数深度的平衡状态。
保证AVL树的左右子树的高度相差最多为 1 有很多种方法,一种常见的方式是引入平衡因子(balance factor),一般将平衡因子定义为一棵树的右子树高度减去左子树的高度的值。
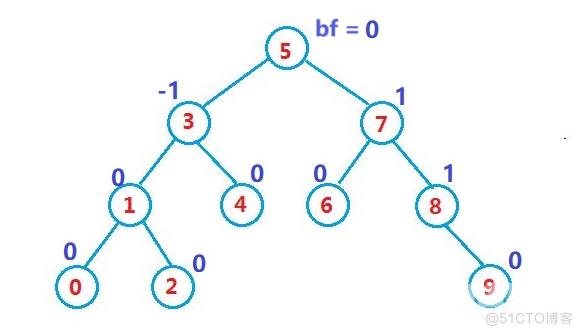
AVL树的定义:
//此处的AVL树是一个Key-Value模型
template<typename Key, typename Value>
struct AVL_tree_node
{
private:
typedef AVL_tree_node<Key, Value> AVLT_node;
public:
std::pair<Key, Value> _kv; //节点数据
AVLT_node* _left;
AVLT_node* _right;
AVLT_node* _parent; //以三叉链形式定义AVL树
int _bf; //balance factor
AVL_tree_node(const std::pair<Key, Value>& kv)
:_kv(kv),
_left(nullptr), _right(nullptr),
_parent(nullptr),
_bf(0)
{ }
};
template<typename Key, typename Value>
class AVL_tree
{
private:
typedef AVL_tree_node<Key, Value> AVLT_node;
public:
AVL_tree()
:_root(nullptr)
{ }
/*…………*/
~AVL_tree()
{
_destroy(_root);
}
private:
void _destroy(AVLT_node* root)
{
if (root == nullptr) {
return;
}
_destroy(root->_left);
_destroy(root->_right);
delete root;
root = nullptr;
}
private:
AVLT_node* _root;
};AVL树的插入
AVL树的插入操作与普通搜索树相似,在插入新元素后,可能不再满足AVL树的条件,此时要对树进行调整,使其重新保持平衡。
新元素的插入只会影响新节点的祖先的平衡(平衡因子)。插入新元素后,根据平衡因子(bf)的定义,对于每一棵子树,各个节点的平衡因子变化情况可能有下面几种情况(parent节点为cur所在节点的父节点):
- 如果新增节点在parent左侧,则parent的平衡因子减 1;
- 如果新增节点在parent右侧,则parent的平衡因子加 1;
- 如果更新后parent的平衡因子为 0,则说明parent所在子树的高度不变,不会再向上影响其他祖先;
- 如果更新后parent的平衡因子从 0 变为 1 或 -1,则说明parent所在子树的高度发生变化且在平衡范围内,此时需要向上继续调整祖先的平衡因子;
- 如果更新后parent的平衡因子为 2 或 -2,说明parent所在子树不再平衡,需要对parent所在的子树进行调整使其重新保持平衡。
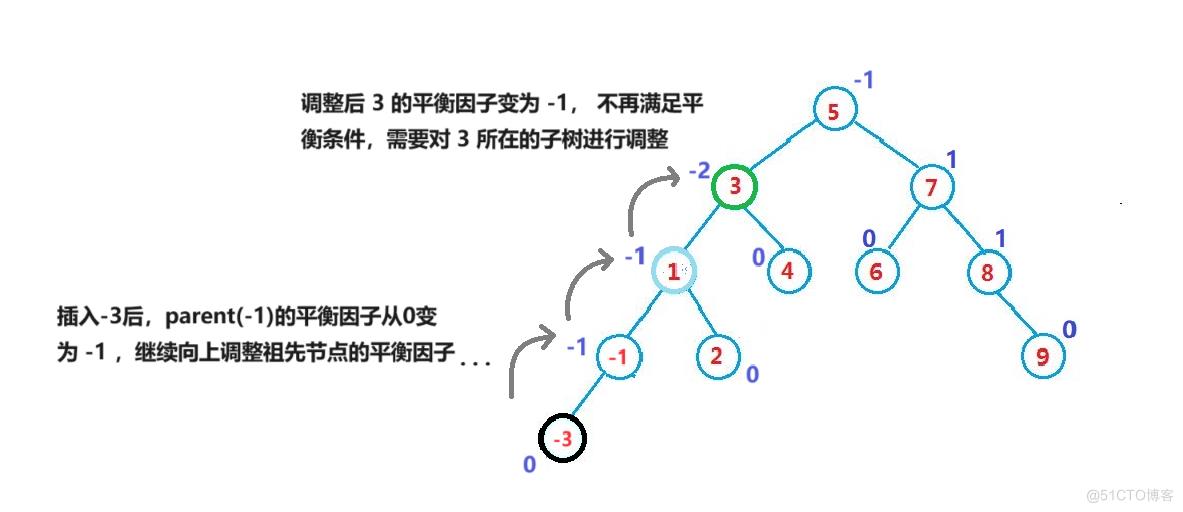
当搜索树不再平衡时,可以通过旋转(rotation)调整解决。
bool insert(const std::pair<Key, Value>& kv)
{
//插入新节点
//检测和调整平衡
//插入新节点时与二叉搜索树一致
AVLT_node* newNode = new AVLT_node(kv);
if (_root == nullptr)
{
_root = newNode;
return true;
}
Key key = kv.first;
AVLT_node* cur = _root;
AVLT_node* parent = nullptr;
while (cur)
{
if (key < cur->_kv.first)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_kv.first)
{
parent = cur;
cur = cur->_right;
}
else {
return false;
}
}
if (key < parent->_kv.first) {
parent->_left = newNode;
}
else {
parent->_right = newNode;
}
newNode->_parent = parent;
cur = newNode;
/*判断和调整平衡*/
}
return true;
}二叉搜索树的旋转
AVL树旋转时遵循的原则为:保证旋转后是依旧是搜索树且降低树的高度。当左子树高时向右旋转,当右子树高时向左旋转。
单旋转
当新节点插入到较高右子树的右侧,或者插入到较高左子树的左侧,这种情况被称为外侧插入(outside insert),可以通过单旋转调整解决。
左单旋
新节点插入到较高右子树的右侧时,此时右子树高于左子树,需要进行左单旋转。
将最深问题节点(parent)的右子树定义为 cur,此时parent的bf值为 2,cur 的 bf 值为 1,则左单旋的关键操作在于将 cur 的左子树作为 parent 的右子树,并将 parent 作为cur的左子树。cur 左侧的所有节点一定小于 parent 的节点值,并且 parent 的节点值一定大于 cur 的节点值,所以原树经过左单旋转操作后依然是搜索树,并且从结果上看,像是将 parent 节点向下压,使其与 cur 的子树等高,使新的父节点(cur)平衡。可以证明,经过旋转后三个关键节点(parent, cur, curRight)的平衡因子都为 0。
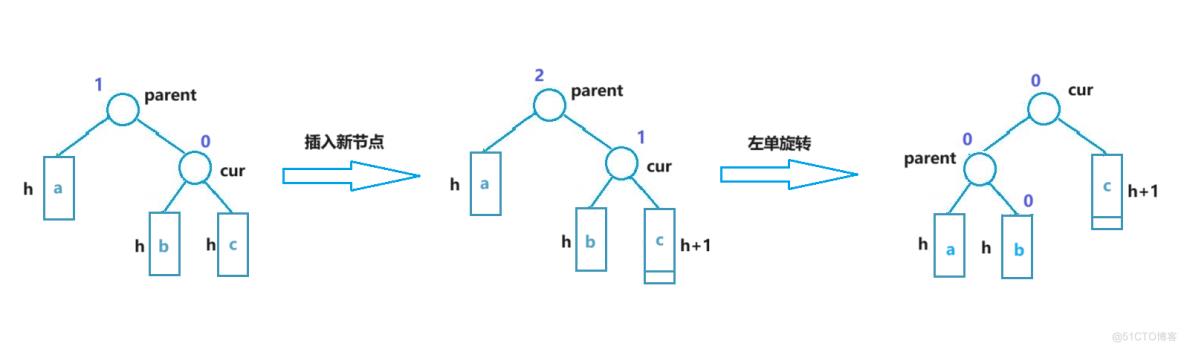
void RotateToLeft(AVLT_node* parent)
{
AVLT_node* cur = parent->_right;
AVLT_node* curLeftNode = cur->_left;
AVLT_node* ppNode = parent->_parent;
parent->_right = curLeftNode; //将cur的左节点作为parent的右节点
cur->_left = parent; //将parent作为cur的左节点
cur->_bf = parent->_bf = 0; //更新bf
//更新父节点
parent->_parent = cur;
if (curLeftNode) {
curLeftNode->_parent = parent;
}
//重新链到AVL树
//parent为_root节点
if (ppNode == nullptr)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (parent == ppNode->_left) {
ppNode->_left = cur;
}
else {
ppNode->_right = cur;
}
cur->_parent = ppNode;
}
}右单旋
当新节点插入到较高左子树的左侧时,此时左子树高于右子树,需要进行右单旋转。右单旋转的具体操作与左单旋转相似,与左单旋转是对称操作。
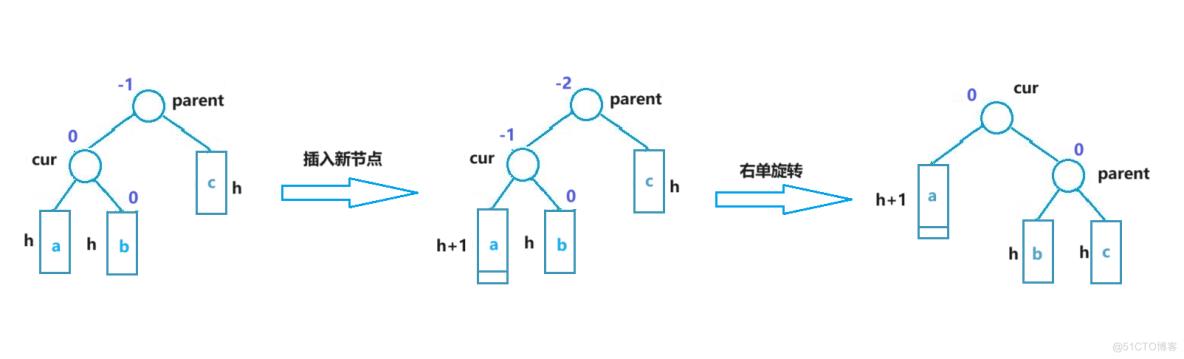
void RotateToRight(AVLT_node* parent)
{
AVLT_node* cur = parent->_left;
AVLT_node* curRight = cur->_right;
AVLT_node* ppNode = parent->_parent;
parent->_left = curRight; //将cur的右节点作为parent的左节点
cur->_right = parent; //将parent作为cur的右节点
cur->_bf = parent->_bf = 0;//更新cur和parent的平衡因子
//更新父节点
parent->_parent = cur;
if (curRight) {
curRight->_parent = parent;
}
//重新整理AVL树
if (ppNode == nullptr)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (parent == ppNode->_left) {
ppNode->_left = cur;
}
else {
ppNode->_right = cur;
}
cur->_parent = ppNode;
}
}从上述对左单旋和右单旋的选择来看,平衡因子本质是用来检测和判断树的平衡情况的。
双旋转
当新节点插入到较高左子树的右侧或者较高右子树的左侧时,这种情况被称为内旋转(inside insert)。此时进行单旋转后搜索树依旧不平衡,无法解决问题,要进行双旋转。
左双旋
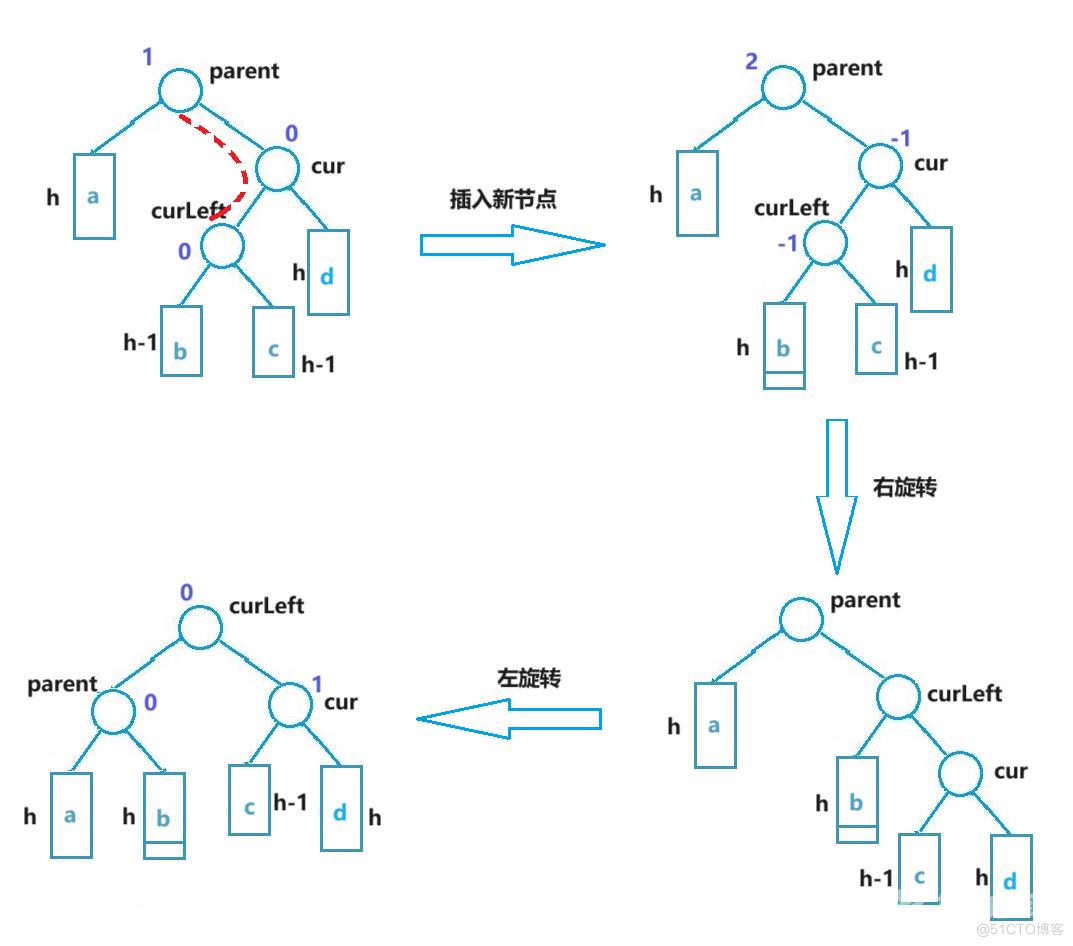
当新节点插入到较高右子树的左侧时,需要进行左双旋。将不平衡子树的根节点作为parent,parent的右子树作为cur,cur的左子树作为curLeft,则左双旋分两步进行:第一步,以cur为根进行右单旋;第二步,以parent为根进行左单旋。完成上述两步操作后,即可使树平衡。
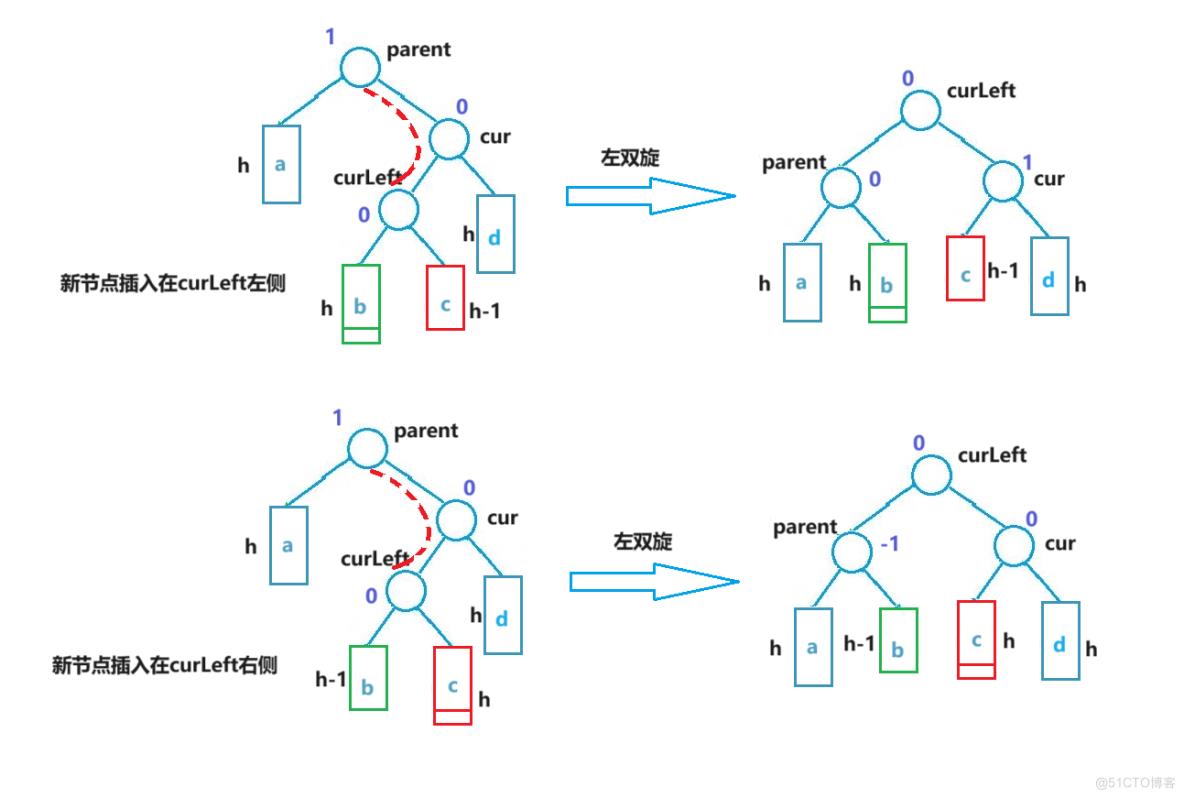
在进行双旋时,如果直接复用上文的左单旋和右单旋接口,则三个关键节点(parent, cur, curLeft)的平衡因子都会被置为 0,这是不正确的,旋转后,三个节点的平衡因子并不一定全部为 0,在进行单旋接口的复用后,需要对三个关键节点的平衡因子进行调整。对平衡因子的调整分两种情况,新节点插入的位置在curLeft左侧、和新节点插入位置在curLeft右侧,从左双旋后的结果来看,左双旋其实是将curLeft的右子树作为cur的左子树,将curLeft的左子树作为parent的右子树,结合新节点插入后curLeft的左右子树的高度变化,可以对三个节点的平衡因子进行判断。
void RotateRightLeft(AVLT_node* parent)
{
AVLT_node* cur = parent->_right;
AVLT_node* curLeft = cur->_left;
int curLeftBf = curLeft->_bf; //根据curLeftBf的旧bf值调整各个节点的bf值
//复用接口时,会将三个转折处的节点的bf一律修改为 0
//这是不完全正确的,需要分情况对三个关键节点的bf值进行修正
RotateToRight(parent->_right);
RotateToLeft(parent);
if (curLeftBf == 0)
{
parent->_bf = 0;
cur->_bf = 0;
curLeft = 0;
} //新节点插入到curLeft的左边
else if (curLeftBf == -1)
{
cur->_bf = 1;
parent->_bf = 0;
curLeft->_bf = 0;
} //新节点插入到curLeft的右边
else if (curLeftBf == 1)
{
parent->_bf = -1;
cur->_bf = 0;
curLeft->_bf = 0;
}
else {
assert(false);
}
}右双旋
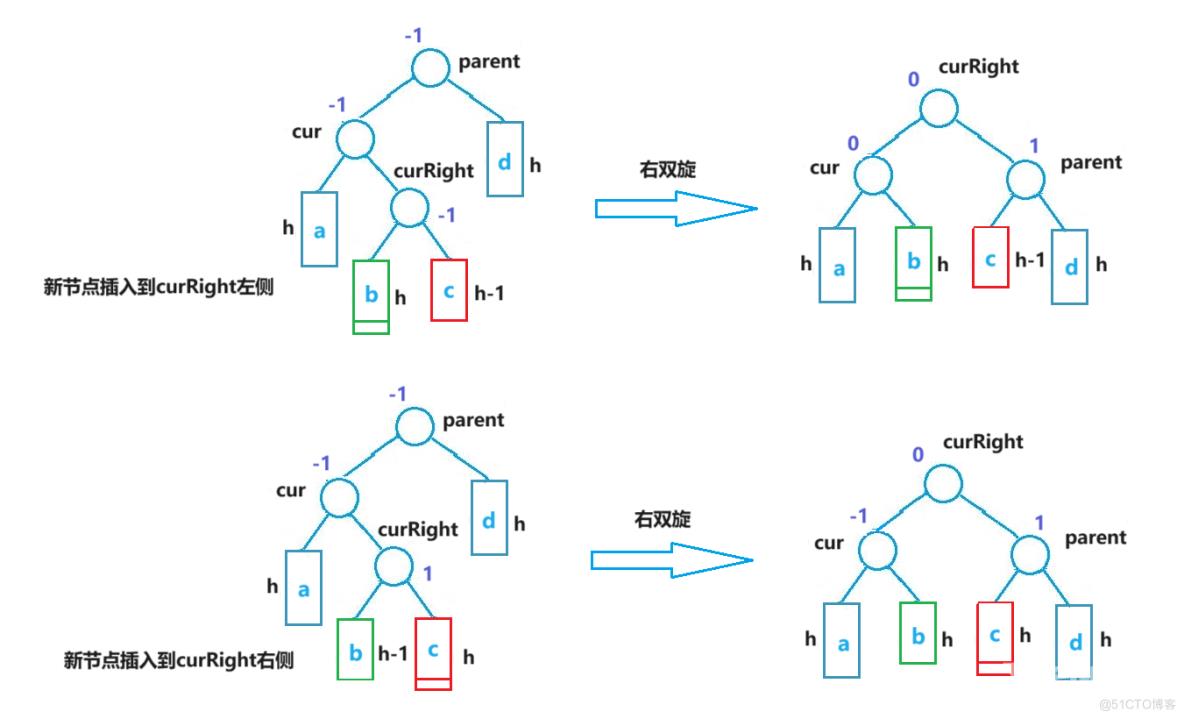
当新节点插入到较高左子树的右侧时,需要进行右双旋。右双旋是与左双旋对称的过程,此处不再对详细过程进行赘述。与左双旋类似,进行右双旋后需要对三个关键节点的平衡因子分两种情况进行调整。
void RotateLeftRight(AVLT_node* parent)
{
AVLT_node* cur = parent->_left;
AVLT_node* curRight = cur->_right;
int curRightBf = curRight->_bf;
RotateToLeft(parent->_left); //以parent的左节点为基准进行左单旋
RotateToRight(parent); //以parnet为基准进行右单旋
//分情况修正三个节点的平衡因子
if (curRightBf == 0)
{
cur->_bf = 0;
parent->_bf = 0;
curRight->_bf = 0;
}
else if (curRightBf == 1)
{
cur->_bf = -1;
parent->_bf = 0;
curRight->_bf = 0;
}
else if (curRightBf == -1)
{
cur->_bf = 0;
parent->_bf = 1;
curRight->_bf = 0;
}
else {
assert(false);
}
}