朋友们好,欢迎来到本期博文 !本期,接着讲解 堆之构建 ! 上一期,末尾之处 !对“完美特性”的证明推导,还留有一处 !下面,仍然用假设法,进行推演 !! 请看下面图解过程
朋友们好,欢迎来到本期博文 !本期,接着讲解 堆之构建 !
上一期,末尾之处 !对“完美特性”的证明推导,还留有一处 !下面,仍然用假设法,进行推演 !!
请看下面图解过程 :>
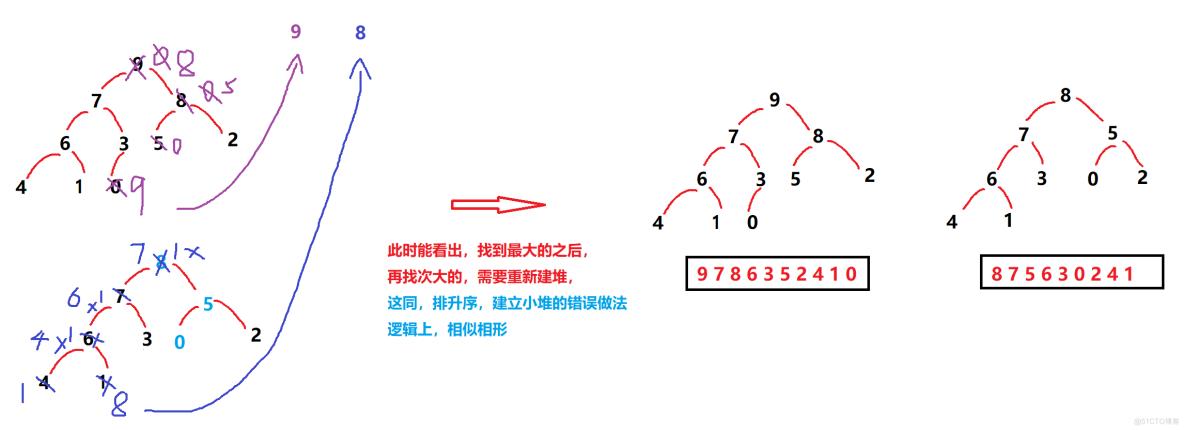
由上图,可以得知,排降序,建立大堆。其弊端在于,将程序遍历的时间复杂度提升到了 O(N * logN)
当最大的数值找到后,每寻找一次 次大的数值,需要一遍又一遍进行建堆操作 !!这样做,显然会使得效率不高,而且时间会不断累积,成本太高了 !
举个例子,在十亿数字之中,寻找出相对大小为前100位次的数,所耗费的时间成本难以估量 !!
出于社会成本的考量,现实世界中,不会采用 排降序,建立大堆 的操作 !!
明明可以用时间复杂度 O(N)遍历一次找到一个目标数值,根本无须重复建立堆区 !
而直接采用,排降序,建立小堆区 即可 !!
以上,二叉树遍历,排升序,排降序,该如何选用不同堆区,又能总结出怎样的优缺点?现已完成推导完成 !!
为了方便老友们,更好地阅读与复习本章节模块,特此 再附上 “完美特性” 的样板图:>

1.反证法,推演 ---> 排升序,建立小堆
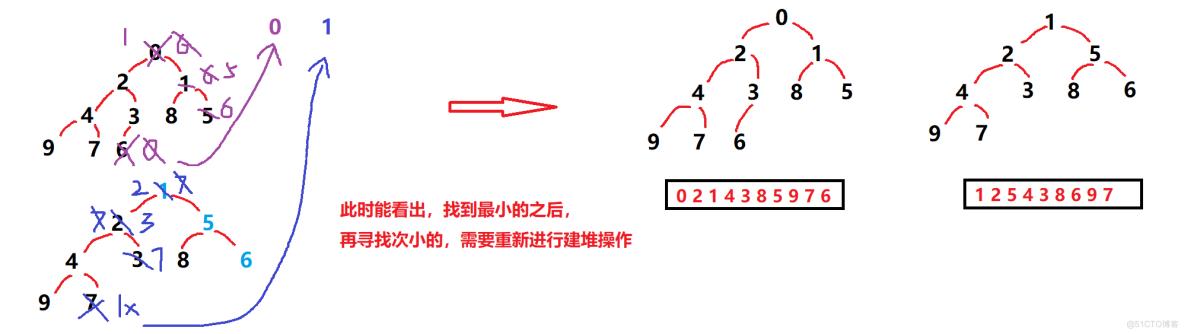
2.反证法,推演 ---> 排降序,建立大堆
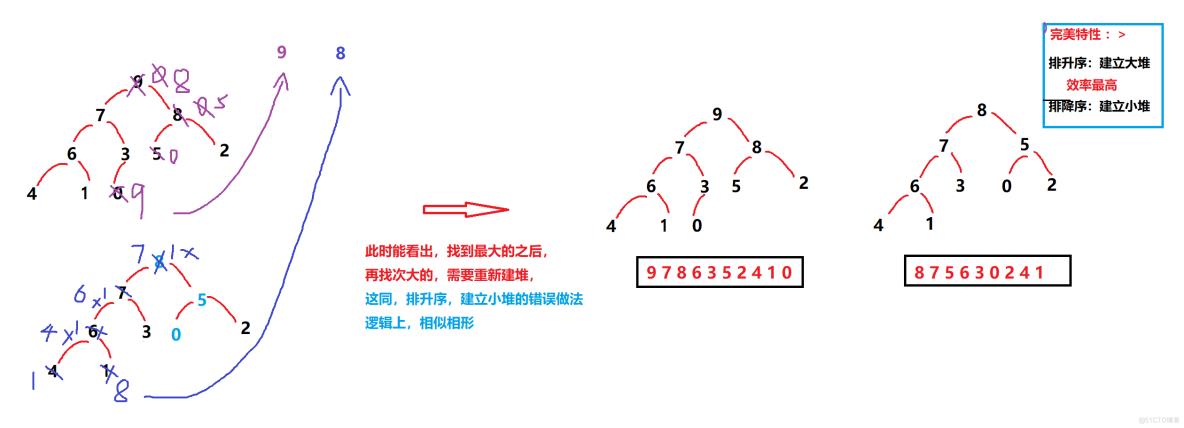
以上就是“完美特性”的补充说明了 !
好了,各位老友!!下面转战 二叉树 --->堆之构建 -->时间复杂度 O(N * logN)证明推导过程 !
其实,先说个题外话,本次时间复杂度的证明,说难不难,说简单不简单 !!
这句话的隐含意思是,本次推导过程,用到了高二数学的知识点,相必大家没忘记 数列综合运用那一块的知识吧
