在大规模场景下的地图构建时候,纯激光雷达传感器无法很好的完成地图构建工作,这时需要考虑使用不同的传感器,获取多种数据来进行传感器的融合,实现位姿的矫正,最终完成复杂大规模场景下的地图构建,这种方法也被称之为多传感器融合。
本篇文章要讲述的是发表在ICRA2020上的一篇多传感器融合实现点云地图构建的文章。
涵盖的知识面有:ESKF,IKF,IMU,Quaternion等。
论文地址:
https://arxiv.org/abs/1907.02233

视频演示


1、论文概览

R-LINS的本质是一个以机器人为中心的激光惯导状态估计器。它使用以下两种传感器来估计机器人的运动姿态:
6轴 IMU:高频,聚焦自身运动,不采集外界环境数据 3D LiDAR:低频,聚焦车体运动,采集外界环境数据 这两种传感器想必大家都不陌生。但是,这两个传感器在复杂大规模领域里,单独的依靠自己的数据是很难实现地图构建的。所以,为了能够在具有挑战性的环境下也能保持鲁棒性和计算效率,本文使用了迭代的误差状态卡尔曼滤波器(ESKF)来通过重复生成新的对应特征来递归的修正机器人的状态信息。
为了防止滤波发散和降低计算成本,本文采用了一种新的以机器人为中心的公式,该公式重新定义了一个移动的局部帧的状态估计量,而不是像标准的以世界为中心的LIO中的固定全局帧的状态估计量。
这里需要注意的是,LINS和LIO的区别如下:

本篇文章相比于LIO,降低了计算的时间消耗,是第一个使用ESKF的LIO框架。

2、雷达里程计分类

现在基于激光雷达里程计的划分主要有三大类:
纯雷达模型 松耦合的LiDAR-IMU模型 紧耦合的LiDAR-IMU模型 下面将依次介绍下对应的模型。
2.1、纯雷达模型
一般来说纯雷达的里程计模型大部分都是基于帧间匹配的,主要分为两大类:
基于迭代最近点法(ICP) 基于正态分布变换(NDT) 所以,现阶段基于迭代最近点法的纯雷达模型,比较出名的是LOAM框架,主要为LOAM和LeGO-LOAM
而基于正态分布变换的纯雷达模型,比较出名的是HDL-Localization。
这些算法都是基于单独的激光雷达传感器数据而进行的里程计推演,实现地图构建。
2.2、松耦合的LiDAR-IMU模型
纯雷达模型使用的传感器是激光雷达,可以很好的探测到外界的环境信息。但是,同样的,也会受到这些信息的干扰,再长时间的运算中会产生一定的累计误差。为了防止这种误差干扰到后续的地图构建中,需要使用另一种传感器来矫正机器人自身的位姿信息。
在实际使用中,为了矫正激光雷达传感器所得到的位姿信息,一般使用的是IMU传感器。
IMU传感器由于是自身运动估计的传感器,所以,采集的都是自身运动的姿态信息。可以很好的矫正激光雷达里程计的位姿信息。所以,通常使用激光雷达和惯导来进行数据融合,实现姿态信息的矫正,这种模型也被称之为LiDAR-Inertial Odometry(LIO) 。
这里主要介绍的是松耦合的LiDAR-IMU模型。
高斯粒子滤波就是比较常见的松耦合模型。
松耦合模型由于是对两个传感器的数据直接进行使用,得到新的姿态解算后的数据,并没有构建新的损失函数,所以,得到的结果相对来说也不是特别的精准。
但是,由于其模型简单,可以快速实现,所以,松耦合的多传感器融合模型,也有着自己的用处。
2.3、紧耦合的LiDAR-IMU模型
紧耦合饿到多传感器融合模型,是将各个传感器的数据都输入到了一个模型之中,构建约束关系,使用优化方法最小化约束,得到最终的结果。其方法可以分为:
基于优化的紧耦合模型 基于EKF的紧耦合模型 基于优化的紧耦合模型目前比较热门的是LIO算法。
基于EKF的紧耦合模型目前比较热门的是LIOM算法。
本文提出的基于迭代ESKF的R-LINS是基于EKF模型的变种的一种紧耦合模型。
由于EKF模型是将非线性模型局部线性化,所以,对于雷达观测约束这种典型的非线性模型而言,容易出现性能低下甚至发散的情况,所以,需要使用一种针对非线性模型的卡尔曼滤波模型来替换EKF。本文使用的是误差状态卡尔曼滤波模型(ESKF)来最小化非线性约束,从而实现姿态的更新,这也是R-LINS的一个创新点。

3、LiDAR-Inertial建图

本章节将着重讲解LiDAR和IMU传感器融合实现地图构建的部分。本文的系统架构如图所示:
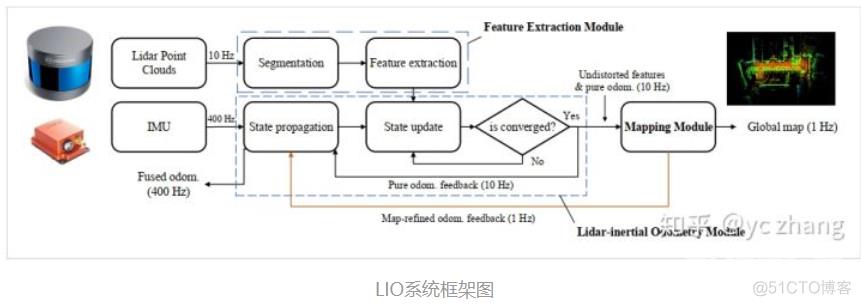
一共分为三大块:
特征提取:从原始点云中提取稳定的特征 LIO:状态传递和状态更新模块组成,使用迭代ESKF,输出纯里程数据和不失真的点云特征 地图构建:细化纯里程数据,得到全局位姿信息并输出全局地图 其中,特征提取使用的是LeGO-LOAM部分的特征提取模块,LIO模块和之前的LIO论文不一样,改变了ESKF作为约束优化的方法,地图构建使用的是LeGO-LOAM部分的地图构建模块。
由于本文的重点是LIO模块,所以,这里直接略过了特征提取和地图构建,只讲解LIO模块的内容。
这里用到了一个迭代卡尔曼滤波。迭代卡尔曼滤波器主要目的在于克服EKF线性化过程中对高阶误差的舍弃而造成的估计不准确。“迭代“主要是指在量测更新过程中添加了一步迭代,直到状态收敛。
3.1、状态定义


这里和VIO中表示使用误差向量中的局部重力不同。我们使用估计的roll和pitch,将重力从世界帧转换到局部帧,来获取重力信息。
本文使用的方法会更加合理一点,假设在极短的时间内,roll和pitch不会急剧变化,则在地图闭环后,得到的结果有着很小的漂移,就可以得到比较精准的重力信息了。
3.2、状态递推


可以推导得到:

其中,有个关系,大家需要注意:
估计值 = 测量值 - 偏差
通过上面的公式(1),我们可以得到

3.3、状态更新
我们知道,卡尔曼滤波(KF)是有着五大方程的,分别是:
预测:状态预测方程,协方差预测方程
更新:状态更新方程,协方差更新方程
卡尔曼增益方程
误差状态卡尔曼滤波(ESKF)也有着上面的五大方程组。唯一的区别在于卡尔曼滤波针对的是物体的运动状态,而误差状态卡尔曼滤波针对的是物体运动状态的误差状态。
在前面3.2部分,我们已经得到了状态预测方程(公式2)和协方差预测方程(公式3)。剩下的就是要得到状态更新方程,协方差更新方程和卡尔曼增益方程了。
本文用的是迭代卡尔曼滤波(IKF)。这里就可以将状态更新问题变成了一个优化问题

这里其实就是LOAM的点线距离和点面距离的公式了:

所以,上面的式子其实可以拆解为:
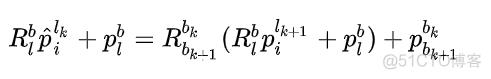
这样看的话,其实就能理解上面公式是什么意思了。
其中,ESKF的卡尔曼增益方程和状态更新方程:

这就是迭代的卡尔曼滤波和常规的卡尔曼滤波的区别之处。
当迭代终止的时候,假定终止下标为 


3.4 状态合成
我们前面算出来的是以机器人为中心的参照系下的位姿信息。所以,为了得到全局坐标信息,需要进行状态合成,合成公式为:

3.5、初始化
我们使用的传感器为IMU和激光雷达,所以有一些参数信息需要提前知晓:


4、地图构建

通过前面的部分,我们已经得到了每个时刻精准的状态估计信息。就可以使用LeGO-LOAM进行地图构建,得到全局地图。
但是也有一些不同。本文使用地图构建模块导出的roll和pitch作为LIO模块的反馈输入,这种策略被证明可以有效地提高系统的鲁棒性。

