
3妹:2哥2哥,你有没有看到新闻, 有人中了2.2亿彩票大奖!
2哥 : 看到了,2.2亿啊, 一生一世也花不完。
3妹:为啥我就中不了呢,不开心呀不开心。
2哥 : 得了吧,你又不买彩票,还是脚踏实地的好~
3妹:小富靠勤,中富靠德,大富靠命, 可能是我命不好。
2哥 : 你哪个是命不好, 你就是想不劳而获,想用最小的体力消耗来暴富吧。
3妹:说到最小体力消耗, 我今天看到一个关相关的题目,让我也来考考你吧~

1题目:
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
示例 1:
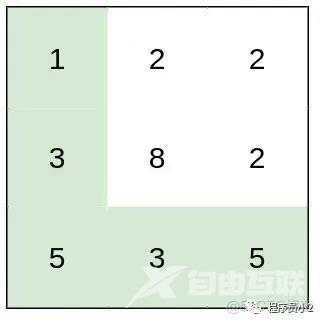
输入:heights = [[1,2,2],[3,8,2],[5,3,5]]
输出:2
解释:路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优,因为另一条路径差值最大值为 3 。
示例 2:
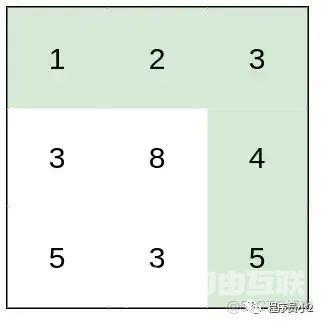
提示:
rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 10^6
2思路:

二分查找,
我们可以将这个问题转化成一个「判定性」问题,即:
是否存在一条从左上角到右下角的路径,其经过的所有边权的最大值不超过 x?
这个判定性问题解决起来并不复杂,我们只要从左上角开始进行深度优先搜索或者广度优先搜索,在搜索的过程中只允许经过边权不超过 x 的边,搜索结束后判断是否能到达右下角即可。
3java代码:
class Solution {
int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public int minimumEffortPath(int[][] heights) {
int m = heights.length;
int n = heights[0].length;
int left = 0, right = 999999, ans = 0;
while (left <= right) {
int mid = (left + right) / 2;
Queue<int[]> queue = new LinkedList<int[]>();
queue.offer(new int[]{0, 0});
boolean[] seen = new boolean[m * n];
seen[0] = true;
while (!queue.isEmpty()) {
int[] cell = queue.poll();
int x = cell[0], y = cell[1];
for (int i = 0; i < 4; ++i) {
int nx = x + dirs[i][0];
int ny = y + dirs[i][1];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && !seen[nx * n + ny] && Math.abs(heights[x][y] - heights[nx][ny]) <= mid) {
queue.offer(new int[]{nx, ny});
seen[nx * n + ny] = true;
}
}
}
if (seen[m * n - 1]) {
ans = mid;
right = mid - 1;
} else {
left = mid + 1;
}
}
return ans;
}
}