算法题:给你两个很大很大的整数(如100位整数),如何求出它们的和? 思路:小学数学竖式拆分,各个击破。 在程序中列出的 “竖式” 究竟是什么样子呢?我们以 426709752318 +95481
算法题:给你两个很大很大的整数(如100位整数),如何求出它们的和?
思路:小学数学竖式拆分,各个击破。

在程序中列出的 “竖式” 究竟是什么样子呢?我们以 426709752318 + 95481253129 为例,来看看大整数相加的详细步骤:
第一步,把整数倒序存储,整数的个位存于数组0下标位置,最高位存于数组长度-1下标位置。之所以倒序存储,更加符合我们从左到右访问数组的习惯。
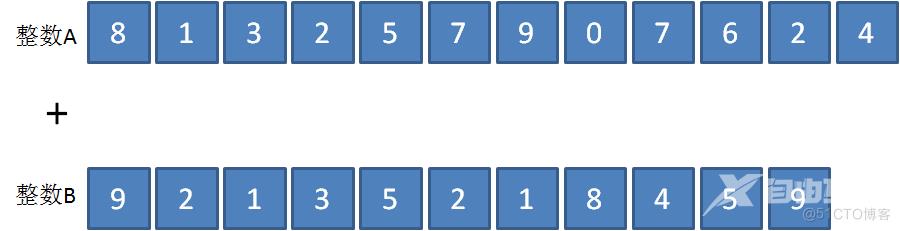
第二步,创建结果数组,结果数组的最大长度是较大整数的位数+1,原因很明显。
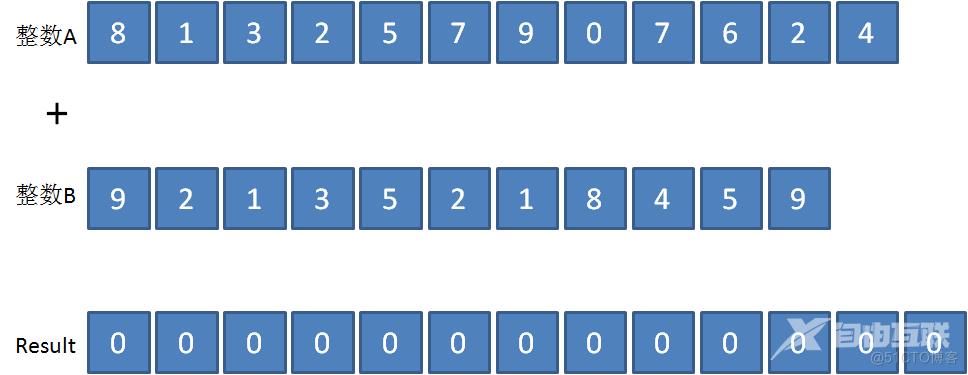
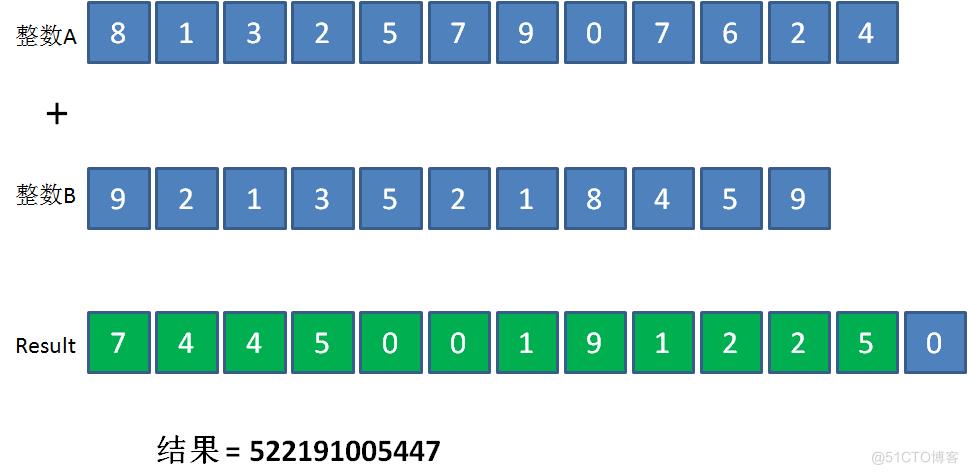
第三步,遍历两个数组,从左到右按照对应下标把元素两两相加,就像小学生计算竖式一样。
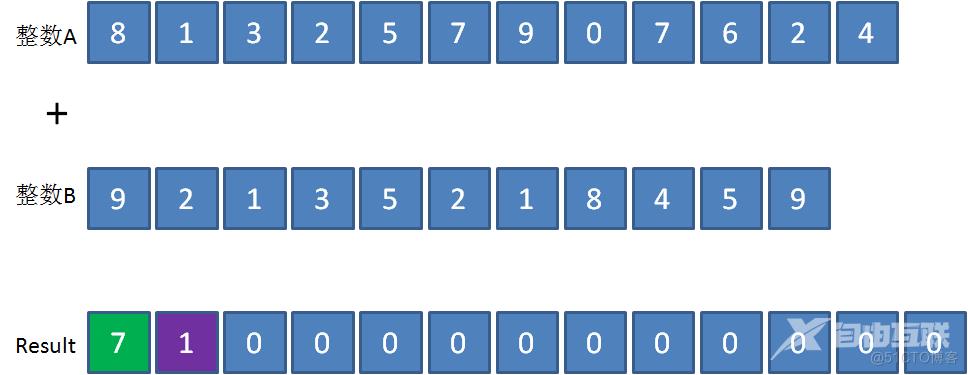
第二组相加的是数组A的第2个元素1和数组B的第2个元素2,结果是3,再加上刚才的进位1,把4填充到Result数组的对应下标:
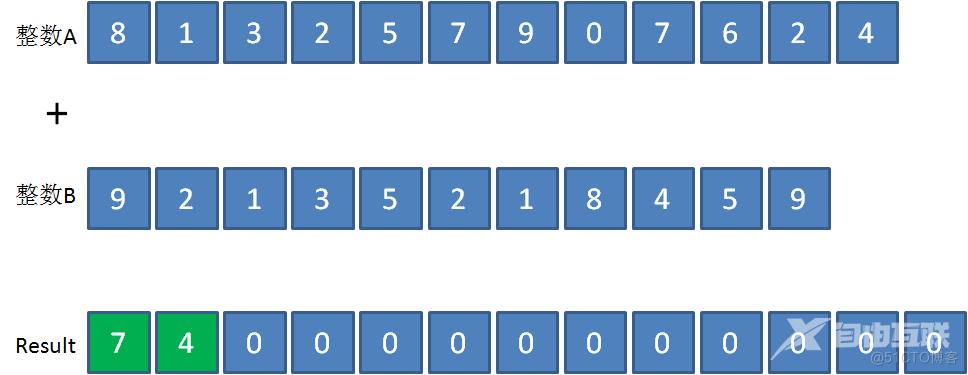
以此类推......一直把数组的所有元素都相加完毕:
第四步,把Result数组的全部元素再次逆序,去掉首位的,就是最终结果:
PHP版本代码如下:
/**
*大整数求和
*@param$bigNumberA 大整数Astring
*@param$bigNumberB 大整数Bstring
*/
function bigNumberSum($bigNumberA,$bigNumberB){
//字符串逆转,拆分为数组
$arrA = $arrB = array();
$lenA = strlen($bigNumberA);
for($i=0;$i<$lenA;$i++){
$arrA[$i] = $bigNumberA[$lenA-$i-1];
}
$lenB = strlen($bigNumberB);
for($i=0;$i<$lenB;$i++){
$arrB[$i] = $bigNumberB[$lenB-$i-1];
}
//1.把两个大整数用数组逆序存储,数组长度等于较大整数位数+1
$maxLength = ($lenA >= $lenB) ? $lenA : $lenB;
$maxLength +=1;
//2.构建result数组,数组长度等于较大整数位数+1,
$arrSum = array();
for($i=0;$i<$maxLength;$i++){
$arrSum[$i] = 0;
}
//3.遍历数组,按位相加
for($i=0;$i<$maxLength;$i++){
//$arrA,$arrB 数组个数不够补0;
if(!isset($arrA[$i])){
$arrA[$i] = 0;
}
if(!isset($arrB[$i])){
$arrB[$i] = 0;
}
$temp = $arrSum[$i];
$temp += $arrA[$i]+$arrB[$i];
//判断是否进位
if($temp >= 10){
$temp = $temp-10;
$arrSum[$i] = $temp;
$arrSum[$i+1] = 1;
}else{
$arrSum[$i] = $temp;
}
}
//var_dump($arrSum);
//4.把result数组再次逆序并转成String
$strSum = '';
for($i=0;$i<$maxLength;$i++){
$strSum .= $arrSum[$maxLength-$i-1];
}
return ltrim($strSum,'0'); //去前导0
}
echo bigNumberSum('426709752318','95481253129');时间复杂度:O(n);
如何优化呢?
我们之前是把大整数按照每一个十进制数位来拆分,比如较大整数的长度有50位,那么我们需要创建一个51位的数组,数组的每个元素存储其中一位。
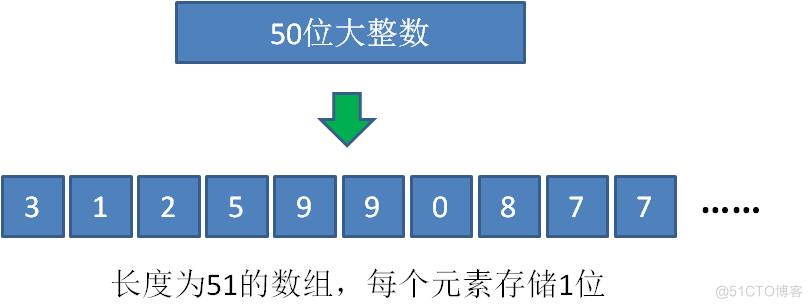
我们真的有必要把原整数拆分得那么细吗?显然不需要,只需要拆分到可以被直接计算的程度就够了。
int类型的取值范围是 -2147483648——2147483647,最多有10位整数。为了防止溢出,我们可以把大整数的每9位作为数组的一个元素,进行加法运算。(这里也可以使用long类型来拆分,按照int范围拆分仅仅是提供一个思路)
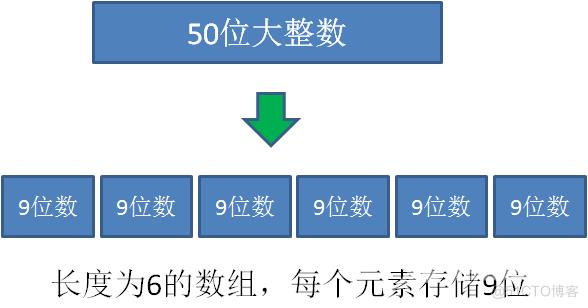
如此一来,占用空间和运算次数,都被压缩了9倍
