分位数回归模型quantile regeression应用详解及示例教程

目录

• 什么是分位数？
• 什么是分位数回归？
• statsmodels中的分位数回归
• 分位数回归与线性回归
• xgboost的分位数回归

普通最小二乘法如何处理异常值？ 它对待一切事物都是一样的——它将它们平方！ 但是对于异常值，平方会显著增加它们对平均值等统计数据的巨大影响。

我们从描述性统计中知道，中位数对异常值的鲁棒性比均值强。 这种理论也可以在预测统计中为我们服务，这正是分位数回归的意义所在——估计中位数（或其他分位数）而不是平均值。 通过选择任何特定的分位数阈值，我们既可以缓和异常值，也可以调整错误的正/负权衡。我们还可以处理需要分位数界限的情况，例如：婴儿的安全出生体重，顶级竞技电子竞技玩家的技能水平，等等。

什么是分位数？

分位数（Quantile），亦称分位点，是指将一个随机变量的概率分布范围分为几个等份的数值点，常用的有中位数（即二分位数）、四分位由3个部分组成(第25、50和75个百分位，常用于箱形图)和百分位数等。

什么是分位数回归？

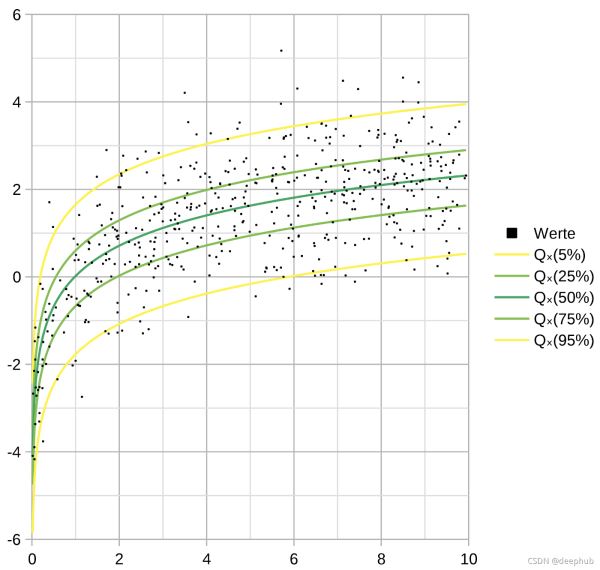
分位数回归是简单的回归，就像普通的最小二乘法一样，但不是最小化平方误差的总和，而是最小化从所选分位数切点产生的绝对误差之和。 如果 q=0.50（中位数），那么分位数回归会出现一个特殊情况 - 最小绝对误差（因为中位数是中心分位数）。我们可以通过调整超参数 q，选择一个适合平衡特定于需要解决问题的误报和漏报的阈值。

statsmodels中的分位数回归

分位数回归是一种不太常见的模型，但 Python中的StatsModel库提供了他的实现。这个库显然受到了R的启发，并从它借鉴了各种语法和API。

StatsModel使用的范例与scikit-learn稍有不同。但是与scikit-learn一样，对于模型对象来说，需要公开一个.fit()方法来实际训练和预测。但是不同的是scikit-learn模型通常将数据(作为X矩阵和y数组)作为.fit()的参数，而StatsModel是在初始化对象时传入数据，而fit方法只传递一些可以调试的超参数。

下面是来自statsmodel的例子(Engel数据集包含在与statmodels中)

%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt

data = sm.datasets.engel.load_pandas().data
mod = smf.quantreg("foodexp ~ income", data)
res = mod.fit(q=0.5)
print(res.summary())

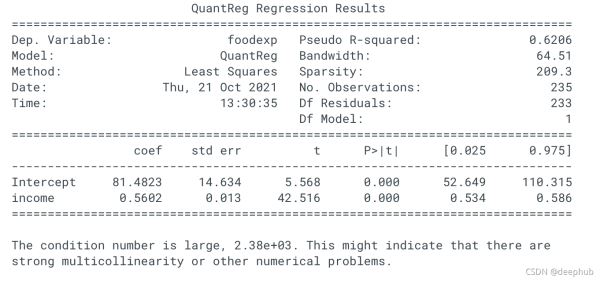
我们可以看看quantile regression model fit的帮助文档：

help(quant_mod.fit)

分位数回归与线性回归

标准最小二乘回归模型仅对响应的条件均值进行建模，并且计算成本较低。 相比之下，分位数回归最常用于对响应的特定条件分位数进行建模。 与最小二乘回归不同，分位数回归不假设响应具有特定的参数分布，也不假设响应具有恒定方差。

下表总结了线性回归和分位数回归之间的一些重要区别：

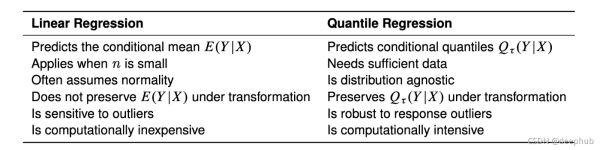
xgboost的分位数回归

最后如果想使用xgboost，又想试试分位数回归，那么可以参考以下代码

class XGBQuantile(XGBRegressor):
  def __init__(self,quant_alpha=0.95,quant_delta = 1.0,quant_thres=1.0,quant_var =1.0,base_score=0.5, booster='gbtree', colsample_bylevel=1,
                colsample_bytree=1, gamma=0, learning_rate=0.1, max_delta_step=0,max_depth=3, min_child_weight=1, missing=None, n_estimators=100,
                n_jobs=1, nthread=None, objective='reg:linear', random_state=0,reg_alpha=0, reg_lambda=1, scale_pos_weight=1, seed=None,silent=True, subsample=1):
    self.quant_alpha = quant_alpha
    self.quant_delta = quant_delta
    self.quant_thres = quant_thres
    self.quant_var = quant_var    
    super().__init__(base_score=base_score, booster=booster, colsample_bylevel=colsample_bylevel,
       colsample_bytree=colsample_bytree, gamma=gamma, learning_rate=learning_rate, max_delta_step=max_delta_step,
       max_depth=max_depth, min_child_weight=min_child_weight, missing=missing, n_estimators=n_estimators,
       n_jobs= n_jobs, nthread=nthread, objective=objective, random_state=random_state,
       reg_alpha=reg_alpha, reg_lambda=reg_lambda, scale_pos_weight=scale_pos_weight, seed=seed,
       silent=silent, subsample=subsample)    
    self.test = None
  
  def fit(self, X, y):
    super().set_params(objective=partial(XGBQuantile.quantile_loss,alpha = self.quant_alpha,delta = self.quant_delta,threshold = self.quant_thres,var = self.quant_var) )
    super().fit(X,y)
    return self
  
  def predict(self,X):
    return super().predict(X)
  
  def score(self, X, y):
    y_pred = super().predict(X)
    score = XGBQuantile.quantile_score(y, y_pred, self.quant_alpha)
    score = 1./score
    return score      
  @staticmethod
  def quantile_loss(y_true,y_pred,alpha,delta,threshold,var):
    x = y_true - y_pred
    grad = (x<(alpha-1.0)*delta)*(1.0-alpha)-  ((x>=(alpha-1.0)*delta)& (x<alpha*delta) )*x/delta-alpha*(x>alpha*delta)
    hess = ((x>=(alpha-1.0)*delta)& (x<alpha*delta) )/delta 
 
    grad = (np.abs(x)<threshold )*grad - (np.abs(x)>=threshold )*(2*np.random.randint(2, size=len(y_true)) -1.0)*var
    hess = (np.abs(x)<threshold )*hess + (np.abs(x)>=threshold )
    return grad, hess
  
  @staticmethod
  def original_quantile_loss(y_true,y_pred,alpha,delta):
    x = y_true - y_pred
    grad = (x<(alpha-1.0)*delta)*(1.0-alpha)-((x>=(alpha-1.0)*delta)& (x<alpha*delta) )*x/delta-alpha*(x>alpha*delta)
    hess = ((x>=(alpha-1.0)*delta)& (x<alpha*delta) )/delta 
    return grad,hess  
  @staticmethod
  def quantile_score(y_true, y_pred, alpha):
    score = XGBQuantile.quantile_cost(x=y_true-y_pred,alpha=alpha)
    score = np.sum(score)
    return score  
  @staticmethod
  def quantile_cost(x, alpha):
    return (alpha-1.0)*x*(x<0)+alpha*x*(x>=0)  
  @staticmethod
  def get_split_gain(gradient,hessian,l=1):
    split_gain = list()
    for i in range(gradient.shape[0]):
      split_gain.append(np.sum(gradient[:i])/(np.sum(hessian[:i])+l)+np.sum(gradient[i:])/(np.sum(hessian[i:])+l)-np.sum(gradient)/(np.sum(hessian)+l) )    
    return np.array(split_gain)

https://gist.github.com/benoitdescamps/af5a8e42d5cfc7981e960e4d559dad19#file-xgboostquantile-py

对于LightGBM这里有一篇详细的实现文章：

http://jmarkhou.com/lgbqr/

以上就是分位数回归quantile regeression详解及示例教程的详细内容，更多关于分位数回归quantile regeression的资料请关注易盾网络其它相关文章！