利用JS实现二叉树遍历算法实例代码

目录

• 前言
• 一、二叉树
• 1.1、遍历二叉树
  
• 1.2、用js表示二叉树
  
• 1.3、前序遍历算法
  
• 1.4、中序遍历算法
  
• 1.5、后序遍历算法
  
• 1.6、按层遍历算法
  
• 二、算法题
• 1.1、二叉树的最大深度
  
• 1.2、二叉树的所有路径
  
• 总结

前言

在计算机科学中, 树(tree) 是一种广泛使用的抽象数据类型(ADT)，是一类非线性数据结构。树在计算机领域得到广泛应用，尤其二叉树最为常用。

树的相关概念：

• 结点：每个元素称为结点
• 树根：根节点
• 度：一个结点含有的子结点的个数称为该结点的度
• 叶子节点：度为0的节点

一、二叉树

概念：每个节点最多含有两个子树的树称为二叉树。

1.1、遍历二叉树

二叉树有两种遍历深度遍历和广度遍历，其中深度遍历有前序、 中序和后序三种遍历方法。 广度遍历就是层次遍历，按层的顺序一层一层遍历。

四种遍历的主要思想：

• 前序：先访问根，然后访问左子树，最后访问右子树，DLR。
• 中序：先访问左子树，然后访问根，最后访问右子树，LDR。
• 后序：先后访问左子树，然后访问右子树，最后访问根，LRD。
• 广度：按层的顺序一层一层遍历。

例如a+b*(c-d)-e/f,该表达式用二叉树表示：

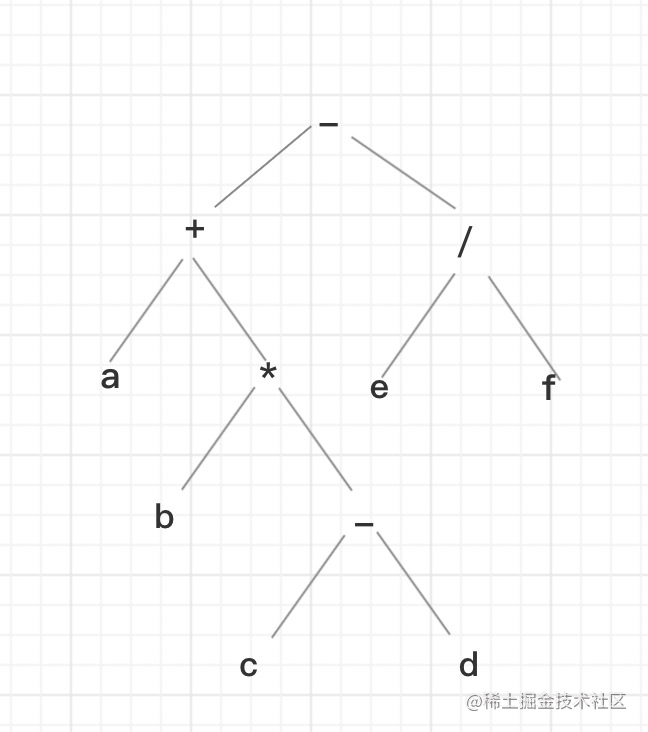
对他分别进行遍历：

• 前序：-+a*b-cd/ef
• 中序：a+b*c-d-e/f
• 后序：abcd-*+ef/-
• 广度：-+/a*efb-cd

1.2、用js表示二叉树

我们用js的对象来表示二叉树，对象拥有三个属性，left、value、right,分别是左子树，值和右子树，上面a+b*(c-d)-e/f的例子我们用js可以这样表示。

var tree = {
    value: '-',
    left: {
        value: '+',
        left: {
            value: 'a'
        },
        right: {
            value: '*',
            left: {
                value: 'b'
            },
            right: {
                value: '-',
                left: {
                    value: 'c'
                },
                right: {
                    value: 'd'
                }
            }
        }
    },
    right: {
        value: '/',
        left: {
            value: 'e'
        },
        right: {
            value: 'd'
        }
    }
}

1.3、前序遍历算法

前序：有两种方法，第一种很简单就是直接使用递归的办法。

function preOrder(treeNode) {
  if(treeNode) {
    console.log(treeNode.value); // 打印出来代表访问这个节点
    preOrder(treeNode.left);
    preOrder(treeNode.right);
  }
}

算法思路很简单，先遍历根节点，然后递归遍历左子树，左子树遍历结束后，递归右子树。

第二种非递归遍历

function preOrder(treeNode) {
  if(treeNode) {
    var stack = [treeNode]; //将二叉树压入栈
    while (stack.length !== 0) {
      treeNode = stack.pop(); // 取栈顶
      document.getElementById('text').appendChild(document.createTextNode(treeNode.value)); // 访问节点
      if(treeNode.right) stack.push(treeNode.right); // 把右子树入栈
      if(treeNode.left) stack.push(treeNode.left); // 把左子树入栈
    }
  }
}

第二种是使用栈的思想，我们都知道，栈是先进后出的一种数据结构，我们先把根节点入栈，然后取栈顶，访问根节点，分别把右左子树入栈，这边必须右边先入栈，因为我们是要先从左边开始访问的，所以右子树先入栈，然后就循环取出栈，直到栈空。

1.4、中序遍历算法

中序递归算法：

function InOrder(treeNode) {
    if(treeNode) {
        InOrder(treeNode.left);
        document.getElementById('text').appendChild(document.createTextNode(treeNode.value));
        InOrder(treeNode.right);
    }
}

和前序递归算法同样的思路，只是访问节点位置不同

第二种：

function InOrder(node) {
  if(node) {
    var stack = [];             // 建空栈
    //如果栈不为空或结点不为空，则循环遍历
    while (stack.length !== 0 || node) { 
      if (node) {               //如果结点不为空
          stack.push(node);     //将结点压入栈
          node = node.left;     //将左子树作为当前结点
      } else {                  //左子树为空，即没有左子树的情况
          node = stack.pop();   //将结点取出来
          document.getElementById('text').appendChild(document.createTextNode(node.value));
          node = node.right;    //将右结点作为当前结点
      }
    }
  }
}

非递归中序算法的思想就是，把当前节点入栈，然后遍历左子树，如果左子树存在就一直入栈，直到左子树为空，访问但前节点，然后让右子树入栈。

1.5、后序遍历算法

第一种：递归遍历算法

function postOrder(node) {
    if (node) { //判断二叉树是否为空
        postOrder(node.left); //递归遍历左子树
        postOrder(node.right); //递归遍历右子树
        document.getElementById('text').appendChild(document.createTextNode(node.value));
    }
}

第二种：非递归遍历算法

function postOrder(node) {
    if (node) { //判断二叉树是否为空
        var stack = [node]; //将二叉树压入栈
        var tmp = null; //定义缓存变量
        while (stack.length !== 0) { //如果栈不为空，则循环遍历
            tmp = stack[stack.length - 1]; //将栈顶的值保存在tmp中
            if (tmp.left && node !== tmp.left && node !== tmp.right) { //如果存在左子树,node !== tmp.left && node !== tmp.righ 是为了避免重复将左右子树入栈
                stack.push(tmp.left);   //将左子树结点压入栈
            } else if (tmp.right && node !== tmp.right) { //如果结点存在右子树
                stack.push(tmp.right);  //将右子树压入栈中
            } else {
                document.getElementById('text').appendChild(document.createTextNode(stack.pop().value));
                node = tmp;
            }
        }
    }
}

这里使用了一个tmp变量来记录上一次出栈、入栈的结点。思路是先把根结点和左树推入栈，然后取出左树，再推入右树，取出，最后取根结点。

下面是用这个算法遍历前面那个二叉树的过程

        stack       tmp         node        打印
初始 ：  -          null         -
第1轮：  -+          -           -
第2轮：  -+a         +           -
第3轮：  -+          a           a            a
第4轮：  -+*         +           a 
第5轮：  -+*b        *           a 
第6轮：  -+*         b           b            b
第7轮：  -+*-        *           b
第8轮：  -+*-c       -           b
第9轮：  -+*-        c           c            c
第10轮： -+*-d       -           c
第11轮： -+*-        d           d            d
第12轮： -+*         -           -            -
第13轮： -+          *           *            *
第14轮： -           +           +            +
第15轮： -/          -           +           
第16轮： -/e         /           +
第17轮： -/          e           e            e
第18轮： -/f         /           e           
第19轮： -/          f           f            f
第20轮： -           /           /            /
第21轮：             -           -            -

结果：abcd-*+ef/-

1.6、按层遍历算法

function breadthTraversal(node) {
    if (node) {                             //判断二叉树是否为空
        var que = [node];                   //将二叉树放入队列
        while (que.length !== 0) {          //判断队列是否为空
            node = que.shift();             //从队列中取出一个结点
            document.getElementById('text').appendChild(document.createTextNode(node.value));   //将取出结点的值保存到数组
            if (node.left) que.push(node.left);   //如果存在左子树，将左子树放入队列
            if (node.right) que.push(node.right); //如果存在右子树，将右子树放入队列
        }
    }
}

使用数组模拟队列，首先将根结点归入队列。当队列不为空时，执行循环：取出队列的一个结点，如果该节点有左子树，则将该节点的左子树存入队列；如果该节点有右子树，则将该节点的右子树存入队列。

二、算法题

1.1、二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

比如下面这个二叉树，返回深度3。

    3
   / \
  9  20
    /  \
   15   7

const tree = {
    value: 3,
    left: {
        value: 9
    },
    right: {
        value: 20,
        left: { value: 15 },
        right: { value: 9 }
    }
}

递归算法：递归算法的思路很简单，先拿到左子树最深层，再拿到右子树最深层，取他们最大值就是树的深度。

var maxDepth = function(root) {
  if (!root) {
    return 0;
  }
  const leftDeep = maxDepth(root.left) + 1;
  const rightDeep = maxDepth(root.right) + 1;
  return Math.max(leftDeep, rightDeep);
};
/*
maxDepth(root) = maxDepth(root.left) + 1  = 2
maxDepth(root.left) = maxDepth(root.left.left) + 1 = 1
maxDepth(root.left.left) = 0;

maxDepth(root) = maxDepth(root.right) + 1 = 3
maxDepth(root.right) = maxDepth(root.right.right) + 1 = 2
maxDepth(root.right.right) = maxDepth(root.right.right.right) + 1 = 1
maxDepth(root.right.right.right) = 0
*/

1.2、二叉树的所有路径

给定一个二叉树，返回所有从根节点到叶子节点的路径。

比如：

    3
   / \
  9  20
    /  \
   15   7
 
返回：['3->9', '3->20->15', '3->20->7']

使用递归的方法：

var binaryTreePaths = function(root) {
  if (!root) return [];
  const res = [];
  function dfs(curNode, curPath) {
    if(!curNode.left && !curNode.right) {
      res.push(curPath);
    }
    if(curNode.left) {
      dfs(curNode.left, `${curPath}->${curNode.left.value}`)
    }
    if(curNode.right) {
      dfs(curNode.right, `${curPath}->${curNode.right.value}`)
    }
  }
  dfs(root, `${root.value}`);
  return res;
};

总结

到此这篇关于利用JS实现二叉树遍历算法的文章就介绍到这了,更多相关JS二叉树遍历算法内容请搜索自由互联以前的文章或继续浏览下面的相关文章希望大家以后多多支持自由互联！