-
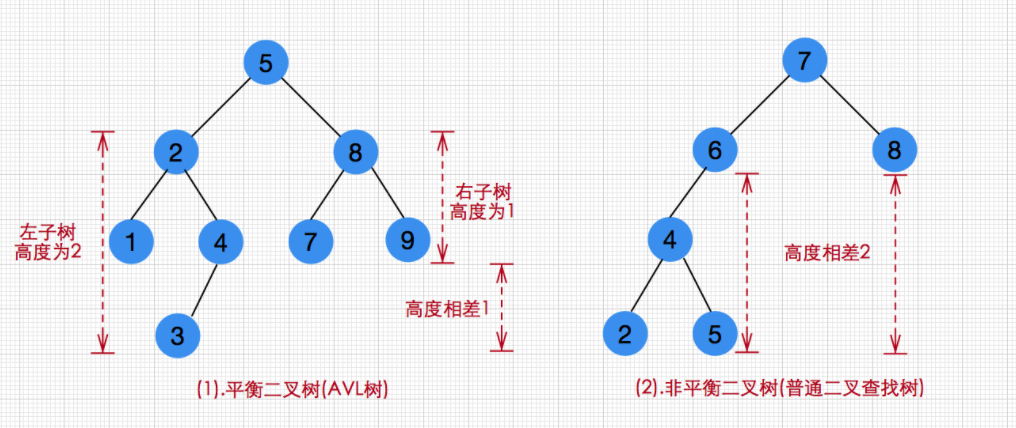
动机:二叉查找树的操作实践复杂度由树高度决定,所以希望控制树高,左右子树尽可能平衡。
-
平衡二叉树(AVL树):称一棵二叉查找树为高度平衡树,当且仅当或由单一外结点组成,或由两个子树形 Ta 和 Tb 组成,并且满足:
- |h(Ta) - h(Tb)| <= 1,其中 h(T) 表示树 T 的高度
- Ta 和 Tb 都是高度平衡树
即:每个结点的左子树和右子树的高度最多差 1 的 二叉查找树。
-
设 T 为高度平衡树中结点 q 的平衡系数为 q 的右子树高度减去左子树高度
-
高度平衡树所以结点的平衡系数只可能为:-1, 0, 1
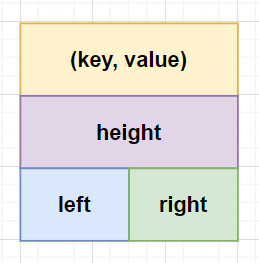
1️⃣ key:关键字的值
2️⃣ value:关键字的存储信息
3️⃣ height:树的高度(只有一个结点的树的高度为 1)
4️⃣ left:左子树根结点的的引用
5️⃣ right:右子树根结点的引用
class AVLNode<K extends Comparable<K>, V> {
public K key;
public V value;
public int height;
public AVLNode<K, V> left;
public AVLNode<K, V> right;
public AVLNode(K key, V value, int height) {
this.key = key;
this.value = value;
this.height = height;
}
}
同二叉查找树的查找算法:【数据结构与算法】手撕二叉查找树
插入算法AVL 树是一种二叉查找树,故可以使用二叉查找树的插入方法插入结点,但插入一个新结点时,有可能破坏 AVL 树的平衡性。
如果发生这种情况,就需要在插入结点后对平衡树进行调整,恢复平衡的性质。实现这种调整的操作称为“旋转”。
在插入一个新结点 X 后,应调整失去平衡的最小子树,即从插入点到根的路径向上找第一个不平衡结点 A。
平衡因子:该结点的左子树高度和右子树高度的差值。如果差值的绝对值小于等于 1,则说明该结点平衡,如果差值的绝对值为 2(不会出现其他情况),则说明该结点不平衡,需要做平衡处理。
造成结点 A 不平衡的的原因以及调整方式有以下几种情况。
LL 型A 结点的平衡因子为 2,说明该结点是最小不平衡结点,需要对 A 结点进行调整。问题发生在 A 结点左子结点的左子结点,所以为 LL 型。
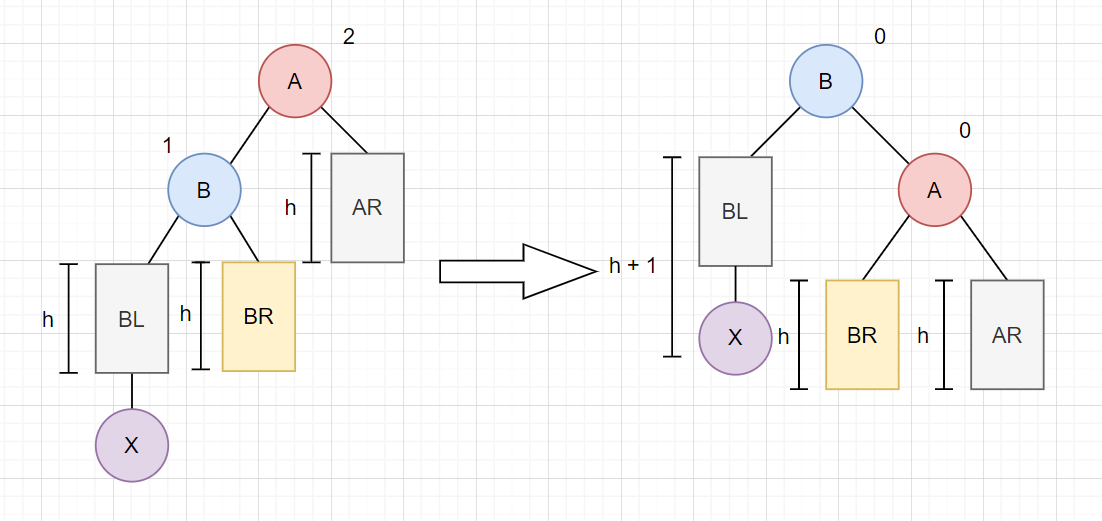
扁担原理:右旋
-
将 A 的左孩子 B 提升为新的根结点;
-
将原来的根结点 A 降为 B 的右孩子;
-
各子树按大小关系连接(BL 和 AR 不变,BR 调整为 A 的左子树)。
-
高度调整:由于调整后 B 的高度依赖于 A 的高度,所以先更新 A 的高度,再更新 B 的高度。
private AVLNode<K, V> rightRotate(AVLNode<K, V> a) {
AVLNode<K, V> b = a.left;
a.left = b.right;
b.right = a;
a.height = Math.max(getHeight(a.left), getHeight(a.right)) + 1;
b.height = Math.max(getHeight(b.left), getHeight(b.left)) + 1;
return b;
}
A 结点的平衡因子为 2,说明该结点是最小不平衡结点,需要对 A 结点进行调整。问题发生在 A 结点右子结点的右子结点,所以为 RR 型。
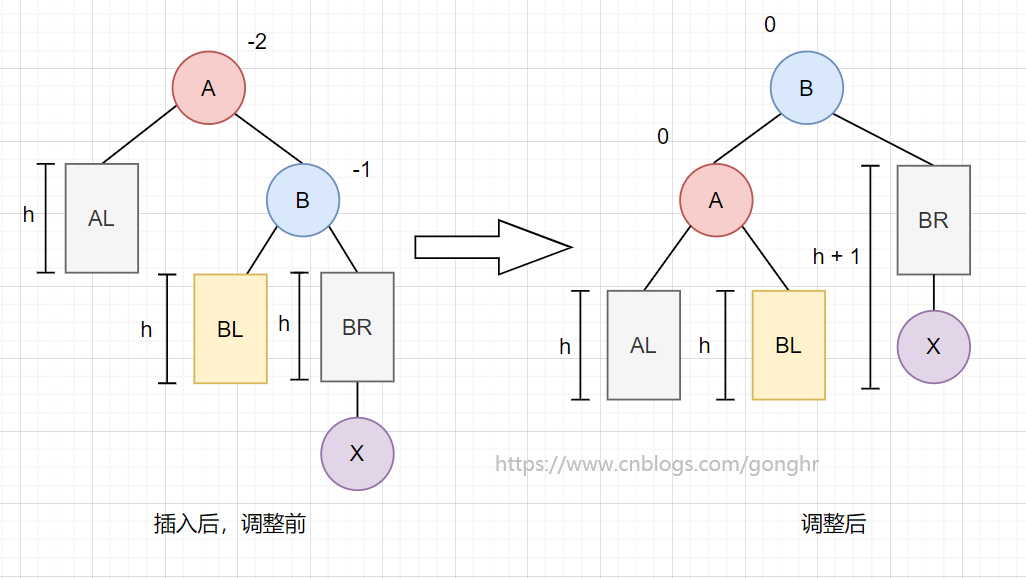
扁担原理:左旋
-
将 A 的右孩子 B 提升为新的根结点;
-
将原来的根结点 A 降为 B 的左孩子;
-
各子树按大小关系连接(AL 和 BR 不变,BL 调整为 A 的右子树)。
-
高度调整:由于调整后 B 的高度依赖于 A 的高度,所以先更新 A 的高度,再更新 B 的高度。
private AVLNode<K, V> leftRotate(AVLNode<K, V> a) {
AVLNode<K, V> b = a.right;
a.right = b.left;
b.left = a;
a.height = Math.max(getHeight(a.left), getHeight(a.right)) + 1;
b.height = Math.max(getHeight(b.left), getHeight(b.left)) + 1;
return b;
}
A 结点的平衡因子为 2,说明该结点是最小不平衡结点,需要对 A 结点进行调整。问题发生在 A 结点左子结点的右子结点,所以为 LR 型。

-
从旋转的角度:对 B 左旋,然后对 A 右旋
-
将 B 的左孩子 C 提升为新的根结点;
-
将原来的根结点 A 降为 C 的右孩子;
-
各子树按大小关系连接(BL 和 AR 不变,CL 和 CR 分别调整为 B 的右子树和 A 的左子树)。
private AVLNode<K, V> leftRightRotate(AVLNode<K, V> a) {
a.left = leftRotate(a.left); // 对 B 左旋
return rightRotate(a); // 对 A 右旋
}
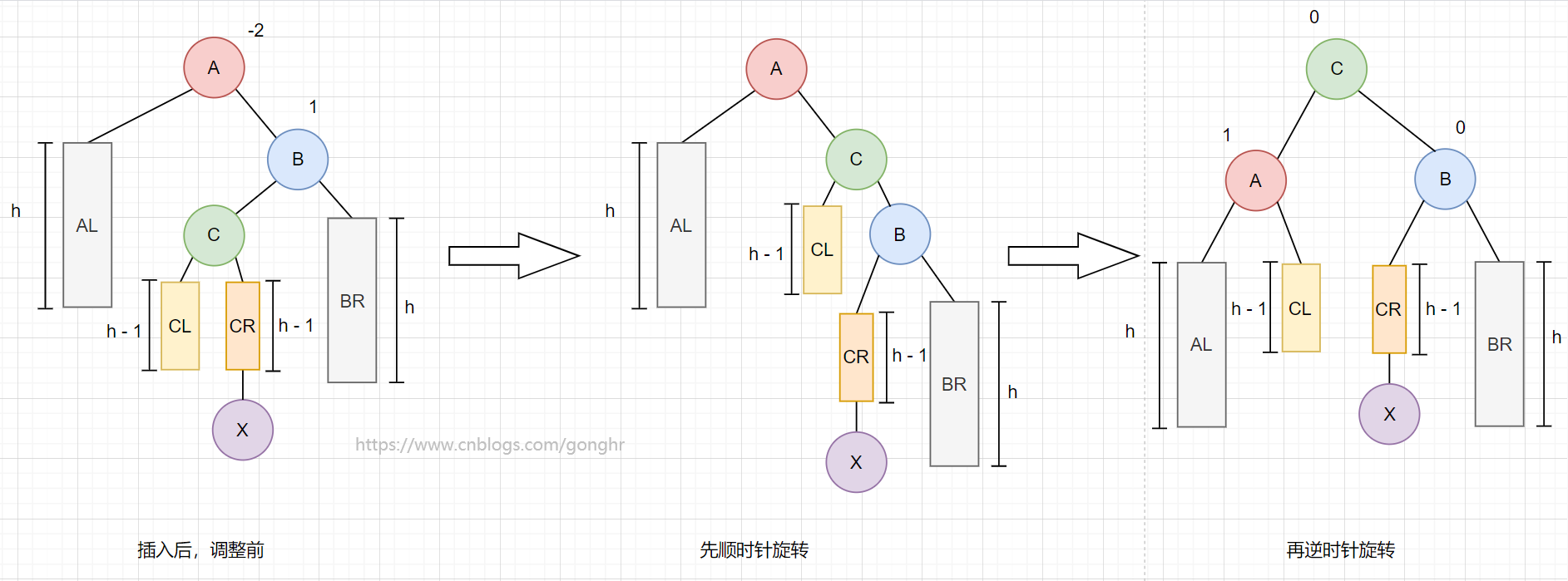
A 结点的平衡因子为 2,说明该结点是最小不平衡结点,需要对 A 结点进行调整。问题发生在 A 结点右子结点的左子结点,所以为 RL 型。
-
从旋转的角度:对 B 右旋,然后对 A 左旋
-
将 B 的左孩子 C 提升为新的根结点;
-
将原来的根结点 A 降为 C 的左孩子;
-
各子树按大小关系连接(AL 和 BR 不变,CL 和 CR 分别调整为 A 的右子树和 B 的左子树)。
private AVLNode<K, V> rightLeftRotate(AVLNode<K, V> a) {
a.right = rightRotate(a.right);
return leftRotate(a);
}
-
根结点默认高度为
1 -
某结点的左右子树高度差的绝对值为
2,则需要进行平衡处理-
左子树高
-
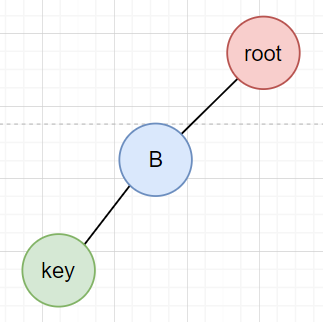
key小于root.left.key:LL型,进行右旋
-
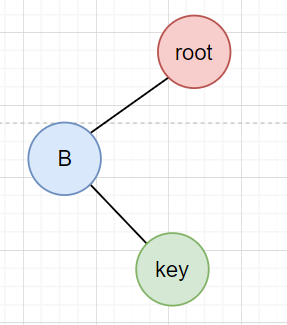
key大于root.left.key:LR型,进行左右旋
-
-
右子树高
-
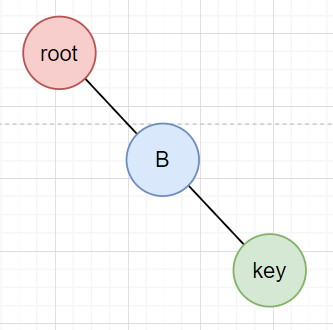
key大于root.right.key:RR型,进行左旋
-
key小于root.right.key:RL型,进行右左旋
-
-
public void insert(K key, V value) {
root = insert(root, key, value);
}
private AVLNode<K, V> insert(AVLNode<K, V> t, K key, V value) {
if (t == null) {
return new AVLNode<>(key, value, 1);
} else if (key.compareTo(t.key) < 0) {
t.left = insert(t.left, key, value);
t.height = Math.max(getHeight(t.left), getHeight(t.right)) + 1;
// 平衡因子判断
if (getHeight(t.left) - getHeight(t.right) == 2) {
if (key.compareTo(t.left.key) < 0) // 左左:右旋
t = rightRotate(t);
else // 左右:先左旋,再右旋
t = leftRightRotate(t);
}
} else if (key.compareTo(t.key) > 0) {
t.right = insert(t.right, key, value);
t.height = Math.max(getHeight(t.left), getHeight(t.right)) + 1;
// 平衡因子判断
if (getHeight(t.left) - getHeight(t.right) == -2) {
if (key.compareTo(t.right.key) > 0) // 右右:左旋
t = leftRotate(t);
else // 右左:先右旋,再左旋
t = rightLeftRotate(t);
}
} else {
t.value = value;
}
return t;
}
-
可采用二叉查找树的删除算法进行删除。
【数据结构与算法】手撕二叉查找树 -
删除某结点 X 后,沿从 X 到根节点的路径上考察沿途结点的平衡系数,若第一个不平衡点为 A,平衡以 A 为根的子树。
-
平衡后,可能使子树 A 高度变小。这样可能导致 A 的父节点不满足平衡性。
-
所以要继续向上考察结点的平衡性,最远可能至根结点,即最多需要做
O(logn)次旋转。 -
对比“插入”操作:平衡 A 后,子树高度不变,A 子树以外的结点不受影响,即插入最多涉及
O(1)次旋转。
