【以下内容仅为本人在学习中的所感所想,本人水平有限目前尚处学习阶段,如有错误及不妥之处还请各位大佬指正,请谅解,谢谢!】
引言
前一篇文章(有关动态规划 - PaperHammer - 自由互联 (cnblogs.com))我们探讨了动态规划及其分析方法,但在做题或面试时往往会需要我们对空间或时间进行优化,尤其是对空间的优化尤为常见。动态规划本就难度较大,对于尚处学习阶段的同学,能写出来就算很不错了。在此,本人将分享我在做题时的想法与见解,并和大家一起学习新的知识,如有错误或更好的思想还请各位大佬留言指正,谢谢!
复杂度分析
复杂度分为时间复杂度与空间复杂度,其不代表程序正真运行时间与所占空间,只反映在执行时间或占用空间随数据规模增大的变化趋势,以最高阶的变化趋势来分别代表整个程序的时空复杂度。
【注:本文重点非复杂度的介绍,相关详细内容将在其他文章中介解释】
(一)空间
空间复杂度取决于我们用来记录之前数据的存储结构。一般地,在DP中常见的空间复杂度有O(N)与O(N2)或者更大,但一般不超过O(N3),通常我们需要对其指数至少减小1或降阶,以达到相应的需求。减少的关键思想在于,判断我们所存储过的数据是否会被再次访问,是否可以不用一直存储。通常采用画表的方式进行判断。
(二)时间
时间复杂度取决于循环结构,而循环结构又取决于推导出的状态转移方程。一般地,常见的时间复杂度为O(N),O(N2)或者更大,但一般不超过O(N3),通常我们需要对其指数至少减小1或降阶。其关键思想在于,一是对某些特殊情况进行判断,使得直接在循环中不进行操作,通常采用逻辑推理方式进行;二是利用某些数据结构和数学理论进行优化。一般地,当我们写出状态转移方程后,就可得出时间复杂度。
优化思路
空间(减少存储结构规模)
(1) 减少变量总数
(2) 减少不必要的数据的存储
时间(减少循环次数)
(1)优化变换状态(从变量的角度,排除无意义或可省去的部分)
(2)选择适当的规划方向(从情况的角度,多种方法对比)
(3)四边形不等式与优化决策单调
第一部分 空间优化
上一篇文章中我们讲到了定变量的过程,我们采用数组的方式存储信息,每个维度的索引代表一个变量,不难发现:变量的数目往往决定了我们存储结构的规模且规模呈次方级增长,虽然空间与时间比起来不那么“宝贵”,现在的设备运存至少也有10 G,但必要的优化还是需要,我们不能因为足够就开始浪费。
题:01背包
【注:在此不重复该题目及方程推导过程,如有需要,请转至上一篇文章(有关动态规划 - PaperHammer - 自由互联 (cnblogs.com))】
方程:f [ i ][ v ] = max(f [ i ][ v ], f [ i-1 ][ v-w[i] ] + c[i]);
或f [ i ] [ j ] = max(f [ i-1 ][ j ], f [ i-1] [ j-w[i] ] + c[i]);
常见的有上述两种形式的方程,其原理是一致的。第一个方程的解释不再赘述;第二个方程中i表示前i件物品,j表示当前背包的容量,f[ i ][ j ]表示在前i件物品中不超过容量j时的最大价值。
例:
输入格式
第一行两个整数 N,V 用空格隔开,分别表示物品数量和背包容积。
接下来有两行,第一行为 wi,第二行为ci 用空格隔开,分别表示第 i 件物品所占的空间和价值。
输入样例
4 20
8 9 5 2
5 6 7 3
输出样例
16
(1)减少不必要的数据的存储
针对第二个方程(第一个类似),我们给出利用上面的例子列出f[ i ][ j ]所每个索引下所对应的值。可以发现i只来源于i-1,即当前状态下的i仅前一次有关,与前两次、前三次均无关。

从表中的数据也可以看出,第i行的数据只依赖于第i-1行的值,因此我们只需用两个一维数组保存第i-1行和第i行这两行的值即可,其中f1[ i ]代表f[ i-1 ][ j ],f2[ i ]表示f[ i ][ j ]。
所以第二个方程可以转化为:f2[ j ] = max(f2[ j ], f1[ j-w[ i ] ] + c[ i ]);
此时,空间复杂度从原来的O(N2)降为了O(N)。
for(int i = 1; i <= n; i++){ for(int j = 1; j <= v; j++){ f2[j] = f1[j]; if(j-c[i] >= 0) f2[j] = max(f2[j], f1[j-w[i]]+c[i]); } for(int k = 1; k <= v; k++) f1[k] = f2[k]; } cout << f2[v] << endl;
(2)减少变量数
但在许多面试题中往往需要我们进行原地修改,那就意味着我们只能使用一个一维数组。同样这道题也可以进行原地修改。但现在的循环顺序是容量从小到大的情况,如果原地修改会出现覆盖数据的情况
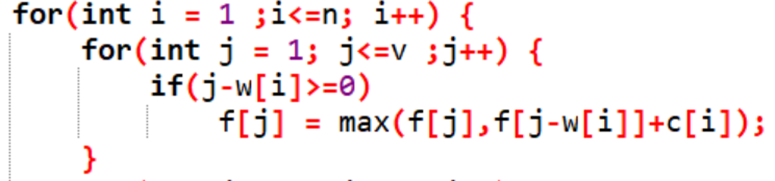
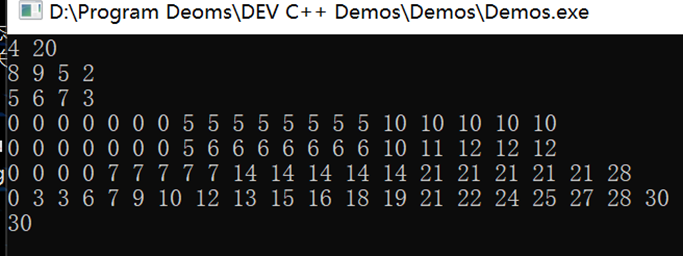
我们来分析一下原因:

当我们使用二维数组时,红色代表i-1行储存的信息,蓝色代表当前第i行的值,该值受到所对应的上一行值的影响。如果我们换成一维数组,从几何意义上其可以反映为:
1.初始状态:整行都为上一次所存储的值
![]()
2.开始更新:根据方程可知,每一个新值受上一个值的影响,即需要上一个值的存在。如果我们依旧从小到大进行更新,那么首先就覆盖了第一个值。之后就会导致我们并没有按照方程原本的意思:根据上一个值计算结果,反而是用新值计算结果,故结果不正确。

所以我们需要将原本正向的更新改为反向,这样就能避免该问题。

for(int i = 1 ;i<=n; i++) { for(int j = v; j>=0 ;j--) if(j-w[i]>=0) f[j] = max(f[j],f[j-w[i]]+c[i]); } cout << f[v] << endl;
第二部分 时间优化
时间往往是我们在编程中更看中的一点,不论是竞赛还是面试,很多情况下都需要对时间的把控。一般来说动态规划在暴力的基础上已经对时间有了很好的优化,但依然可以再优化下面还是通过例子来讲述这两种方法。
题:传纸条
来源:P1006 [NOIP2008 提高组] 传纸条 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
将题目抽象化后可翻译为:从点(1,1)走到(m,n)再从(m,n)回到(1,1)方向只能向下(上)或向右(左),即起点在左上角,终点在右下角。且每个点只能走一次,每个点上有一个正数,返回所有在两次行走的可行路径中的数值的最大和。
往返路径且往返过程等价,不妨将其看为从同一点出发的两条路径。利用上一篇文章的方法步骤,把每次选择怎么走作为一个子问题,并且总是以最大和为基础进行操作,每次选择处理相同。
对于第一条路上的点(i,j)有两种选择方式;
对于第二条路上的点(k,l)有两种选择方式;
选择方式的两种理解:(从左边到达,从上边到达)/(向右走,向下走)
由于二者等价所以合并后对于点(i,j,k,l)有四种选择方式
不难推出方程:f[ i ][ j ][ k ][ l ] = max( f[ i ][ j-1 ][ k-1 ][ l ] , f[ i-1 ][ j ][ k ][ l-1 ] , f[ i ][ j-1 ][ k ][ l-1 ] , f[ i-1 ][ j ][ k-1 ][ l ] ) + value[ i ][ j ] + value[ k ][ l ];为了避免重复每次特判即可,详细内容见文末附录。
根据上述方程可以得到此时的时间复杂度为O(N2*M2),理论上只能承受N,M<=50的数据量,甚至更小。
for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) for (int p = 1; p <= n; p++) for (int q = 1; q <= m; q++) { f[i][j][p][q] = max(max(f[i - 1][j][p - 1][q], f[i - 1][j][p][q - 1]), max(f[i][j - 1][p - 1][q], f[i][j - 1][p][q - 1])) + g[i][j] + g[p][q]; if (i == p && j == q)f[i][j][p][q] -= g[i][j]; //去重,只需判断第二次走的点是否被第一次所走过,因为两条路经本身不会经过自己走过的点,只可能两条路相交 }
(1)优化状态(重新构建变量的意义,改进状态表示)
三维DP:刚刚提到,两个路径的行进是完全等价的,每条路径在每个点只有两种选择,且它们是同步进行的,所以可以得到当前总步数steps = i + j = k + l;利用这一点,我们枚举当前走过的步数,同时枚举第一条路径和第二条路径当前的横坐标或者纵坐标,f[k][i][j]表示走了k步,第一条路径走到第i行,第二条路径走到第j行的最大价值,于是方程转变为:f[ k ][ i ][ j ] = max ( f[ k-1 ][ i ][ j ], f[ k-1 ][ i-1 ][ j-1 ], f[ k-1 ][ i ][ j-1 ], f[ k-1 ][ i-1 ][ j ] ) + value[ i ][ k-i+1 ] + a[ j ][ k-j+1 ];
此时,方程时间复杂度为O(N2 * (N+M))
for (int k = 1; k <= n + m-1; k++) for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) { if ( k-i + 1 < 1 || k - j + 1 < 1) //判断纵坐标的合法性,不合法就跳过 continue; f[k][i][j] = max(max(f[k - 1][i][j], f[k - 1][i - 1][j - 1]), max(f[k - 1][i][j - 1], f[k - 1][i - 1][j])) + g[i][k - i + 1] + g[j][k - j + 1]; if (i == j) f[k][i][j] -= g[i][k - i + 1]; }
二维DP:沿用01背包的优化思想,当前状态与前一个状态有关,所以我们原地修改,反向更新,即可再降一维。
for(int k=3;k<=n+m;k++) for(int i=n;i>=1;i--) for(int p=n;p>i;p--) f[i][p]=max(max(f[i][p],f[i-1][p-1]),max(f[i-1][p],f[i][p-1]))+g[i][k-i]+g[p][k-p];
(2)选择适当的规划方向
动态规划的规划方向主要有两种:顺推和逆推。有些情况下,不同的规划方向,时间效率有所不同。一般地,若初始状态确定,目标状态不确定,“从因到果”,则应考虑采用顺推;反之,若目标状态确定,而初始状态不确定,“从果到因”,就应该考虑采用逆推。若初始状态和目标状态都已确定,一般情况下顺推和逆推都可以选用。但是,我们还可以使用类似双指针一样的思想,进行双向规划,即双线程。
题:传纸条——三维DP
其实,刚才的三维DP已经体现了双线程的思想,即同时进行,本质就是对四维DP的优化
【注:下方内容,即第(3)点在此仅作为补充说明,本人尚未对其深入了解与研究,仅供参考】
(3)四边形不等式与优化决策单调
该方法实际上是基于数学理论推导而来。
有关四边形不等式,它可以针对形如f[ i, j ] = min/max{ m( i, k-1 ), m( k, j) } + w( i, j ) (i ≤ k ≤ j)的方程进行降阶优化。
补充说明:
- a. 区间包含的单调性:对于i ≤ i' < j ≤ j',有w( i' , j ) ≤ w( i , j' ),称w具有区间包含的单调性,即保号性,区间小则对应值就小。
- b. 四边形不等式:对于i ≤ i' < j ≤ j',有w( i , j ) + w( i' , j' ) ≤ w( i' , j ) + w( i , j' ),称函数w满足四边形不等式,即小区间与大区间之和<=交错区间和。
- c. 定理一:如果上述w同时满足区间包含单调性和四边形不等式,那么m也满足四边形不等式性质。
- d. 定理二:如m满足四边形不等式,则s( i , j )单调,即s( i , j ) ≤ s( i , j+1 ) ≤ s( i+1 , j+1 )。其中,s表示m去最优值时的下标。
【注:相关证明过程在此不提供】
由此,我们可以得到:s[ i , j-1 ] ≤ s[ i , j ] ≤ s[ i+1 , j ];
所以上述方程转变为:f[ i , j ] = min/max{ m[ i , k ] + m[ k , j ]} (s[ i , j-1 ] ≤ k ≤ s[ i+1 , j ]);
此时,时间复杂度从O(N3)减小为O(N2)
总结
动态规划的优化还有许多类型,本人目前仅了解以上内容,每一种优化思想都有独特的地方,但这些思想往往十分复杂让人望而生畏,只有通过平时一道题一道题的磨砺,才能逐渐领悟。众所周知,写出代码不难,难的是如何对现有代码进行优化,当我们能够对我们所写过的代码提供一份优化方案时,相信我们的水平一定上了一个台阶,让我们一起努力,加油!
【感谢您可以抽出时间阅读到这里,内容可能会有许多不妥之处;受限于水平,许多地方可能存在错误,还请各位大佬留言指正,请见谅,谢谢!】
#附文中所提到的2个题目的代码(仅提供文中提到的部分方案,可满足绝大多数时的要求)
(1)01背包
#include <bits/stdc++.h> using namespace std; int n,v,c[102],w[102],f[100000]; int main() { cin >> n >> v; for(int i = 1; i <= n; i++) cin >> w[i]; for(int i = 1; i <= n; i++) cin >> c[i]; for(int i = 1; i <= n; i++) { for(int j = 1; j <= v; j++) { if(j - w[i] >= 0) f[j] = max(f[j], f[j - w[i]] + c[i]); } } cout<<f[v]<<endl; return 0; }
(2)传纸条(三维DP)
#include<bits/stdc++.h> using namespace std; int n, m, g[54][54], f[108][54][54]; int main() { ios::sync_with_stdio(false); cin >> n >> m; for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) cin >> g[i][j]; for (int k = 1; k <= n + m-1; k++) for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) { if ( k-i + 1 < 1 || k - j + 1 < 1) //判断纵坐标的合法性,不合法就跳过 continue; f[k][i][j] = max(max(f[k - 1][i][j], f[k - 1][i - 1][j - 1]), max(f[k - 1][i][j - 1], f[k - 1][i - 1][j])) + g[i][k - i + 1] + g[j][k - j + 1]; if (i == j) f[k][i][j] -= g[i][k - i + 1]; } cout << f[n + m - 1][n][n] << endl; return 0; }
(3)传纸条(二维DP)
#include<bits/stdc++.h> using namespace std; int n, m, g[54][54], f[108][108]; int main() { ios::sync_with_stdio(false); cin >> n >> m; for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) cin >> g[i][j]; for(int k=3;k<=n+m;k++) for(int i=n;i>=1;i--) for(int p=n;p>i;p--) f[i][p]=max(max(f[i][p],f[i-1][p-1]),max(f[i-1][p],f[i][p-1]))+g[i][k-i]+g[p][k-p]; cout << f[n - 1][n] << endl; return 0; }TRANSLATE with
