Python 一网打尽＜排序算法＞之从希尔排序算法的分治哲学开始

1. 前言

本文将介绍希尔排序、归并排序、基数排序（桶排序）。

在所有的排序算法中，冒泡、插入、选择属于相类似的排序算法，这类算法的共同点：通过不停地比较，再使用交换逻辑重新确定数据的位置。

希尔、归并、快速排序算法也可归为同一类，它们的共同点都是建立在分治思想之上。把大问题分拆成小问题，解决所有小问题后，再合并每一个小问题的结果，最终得到对原始问题的解答。

通俗而言：化整为零，各个击破。

分治算法很有哲学蕴味：老祖宗所言 合久必分，分久必合，分开地目的是为了更好的合并。

分治算法的求解流程：

• 分解问题：将一个需要解决的、看起很复杂 原始问题 分拆成很多独立的子问题，子问题与原始问题有相似性。

  如：一个数列的局部（小问题）有序，必然会让数列最终（原始问题）有序。

• 求解子问题：子问题除了与原始问题具有相似性，也具有独立性，即所有子问题都可以独立求解。

• 合并子问题：合并每一个子问题的求解结果最终可以得到原始问题的解。

下面通过深入了解希尔排序算法，看看分治算法是如何以哲学之美的方式工作的。

2. 希尔排序

讲解希尔之前，先要回顾一下插入排序。插入排序的平均时间复杂度，理论上而言和冒泡排序是一样的 O（n²），但如果数列是前部分有序，则每一轮只需比较一次，对于 n 个数字的原始数列而言，时间复杂度可以是达到 O(n)。

插入排序的时间复杂度为什么会出现如此有意思的变化？

• 插入排序算法的排序思想是尽可能减少数字之间的交换次数。
• 通常情形下，交换处理的时间大约是移动的 3 倍。这便是插入排序的性能有可能要优于冒泡排序的原因。

希尔排序算法本质就是插入排序，或说是对插入排序的改良。

其算法理念：让原始数列不断趋近于排序，从而降低插入排序的时间复杂度。

希尔排序的实现流程：

• 把原始数列从逻辑上切割成诸多个子数列。
• 对每一个子数列使用插入排序算法排序。
• 当所有子数列完成后，再对原数列进行最后一次插入算法排序。

希尔排序算法的理念：当数列局部有序时，全局必然是趋向于有序”。

希尔排序的关键在于如何切分子数列，切分方式可以有 2 种：

任何时候使用分治理念解决问题时，分拆子问题都是关键的也是核心的。

2.1 前后切分

如有原始数列=[3，9，8，1，6，5，7] 采用前后分成 2 个子数列。

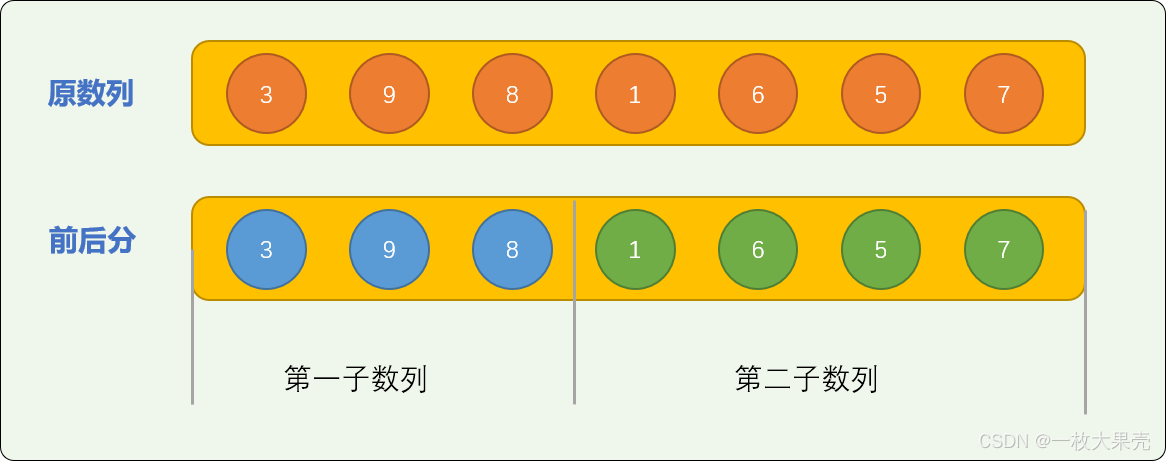
前后分算得上是简单粗暴的切分方案，没有太多技术含量，这种一根筋的切分方式，对于原始问题的最终性能优化可能起不了太多影响。

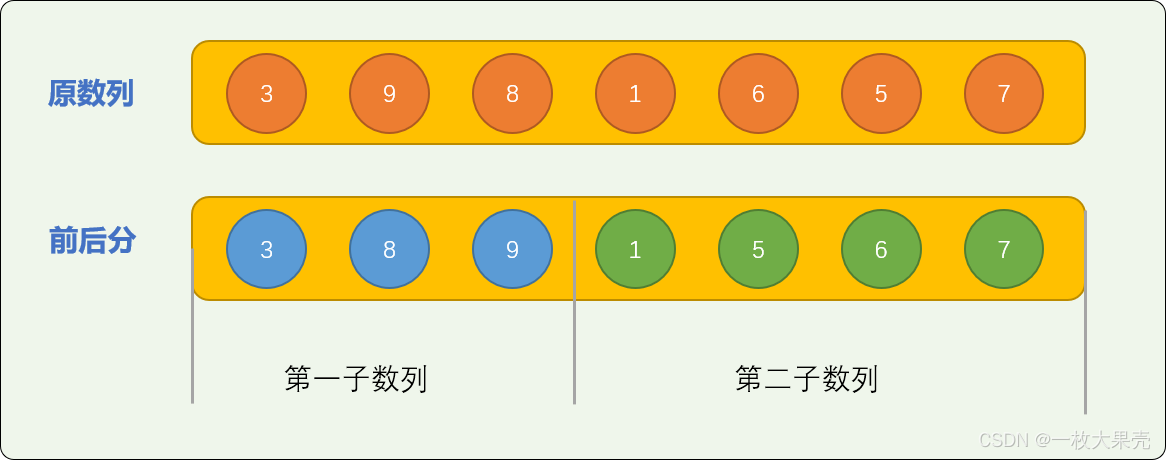
如上图所示，对子数列排序后，如果要实现原始数列中的所有数字从小到大排列有序，则后部分的数字差不多全部要移到时前部分数字的中间，其移动量是非常大的。

后面的 4 个数字中，1 需要移动 3 次，5、6、7 需要移动 2 次， 肉眼可见的次数是 9 次。

这种分法很难实现数字局部有序的正态分布，因为数字的位置变化不大。

如下图是原始数列=[3，9，8，1，6，5，7] 的原始位置示意图：

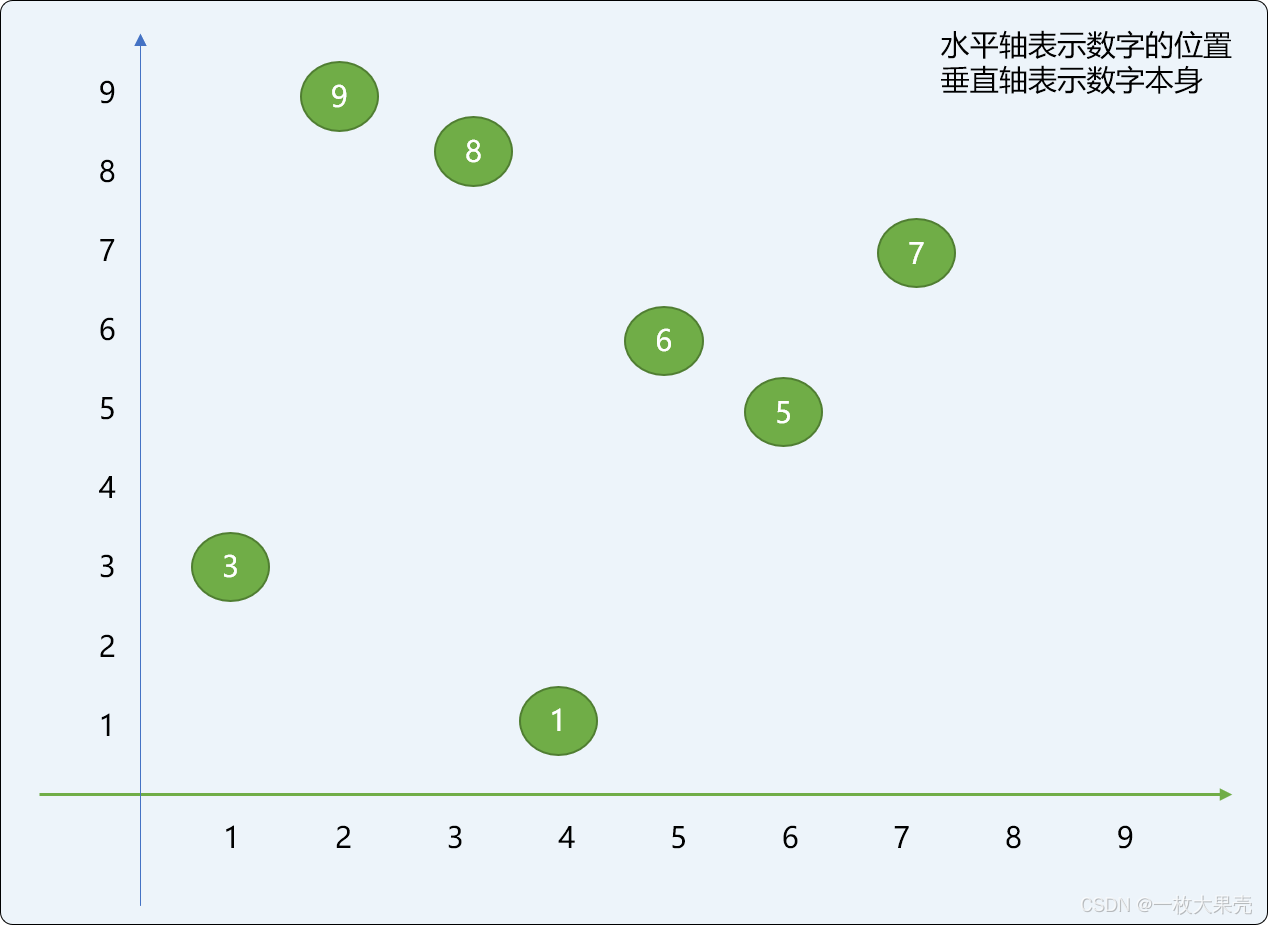
使用前后切分后的数字位置变化如下图所示，和上图相比较，数字的位置变化非常有限，而且是限定在一个很窄的范围内。也就是说子问题的求解结果对最终问题的结果的影响很微小。

2.2 增量切分

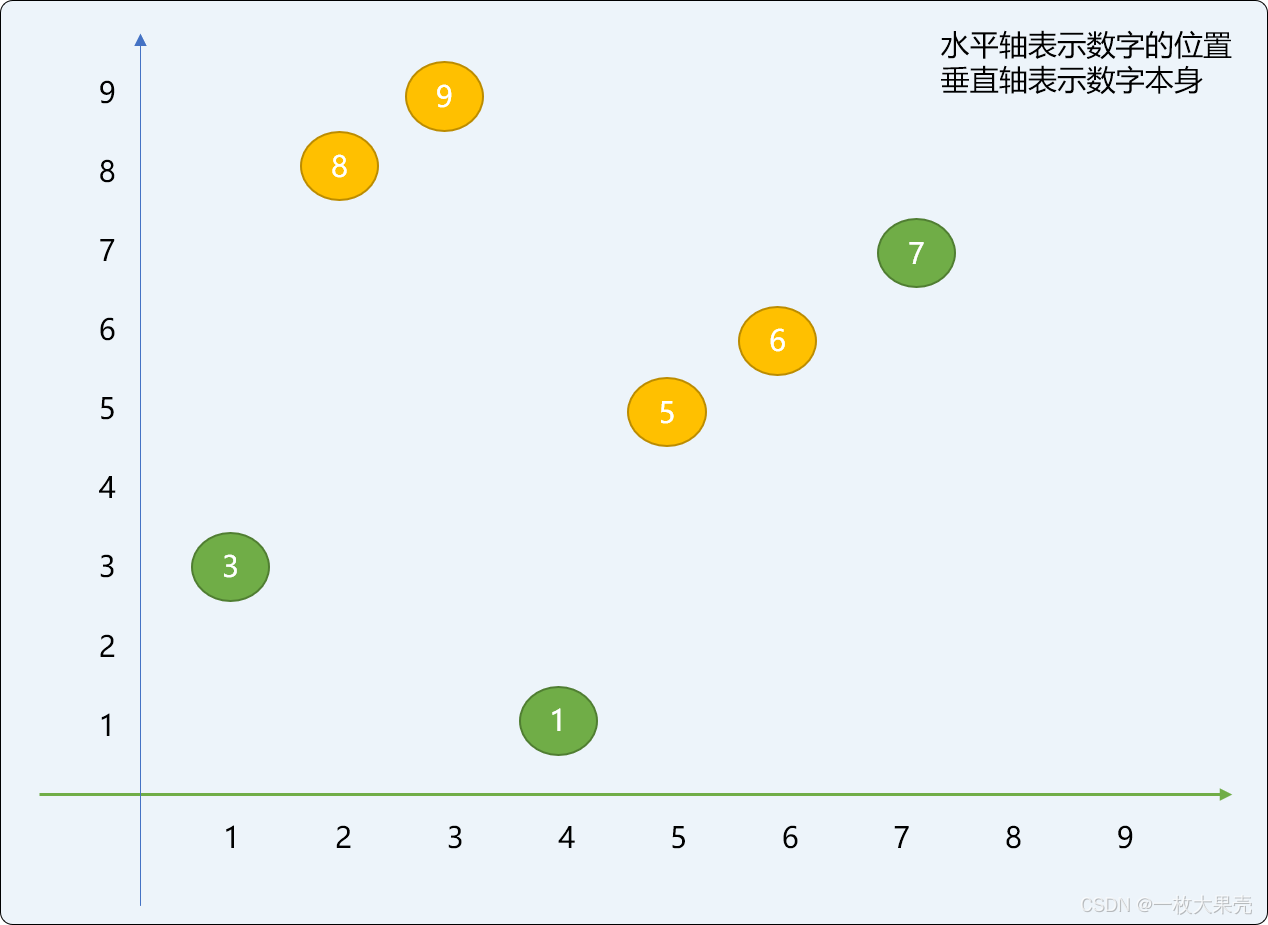
增量切分采用间隔切分方案，可能让数字局部有序以正态分布。

增量切分，需要先设定一个增量值。如对原始数列=[3，9，8，1，6，5，7] 设置切分增量为 3 时，整个数列会被切分成 3 个逻辑子数列。增量数也决定最后能切分多少个子数列。

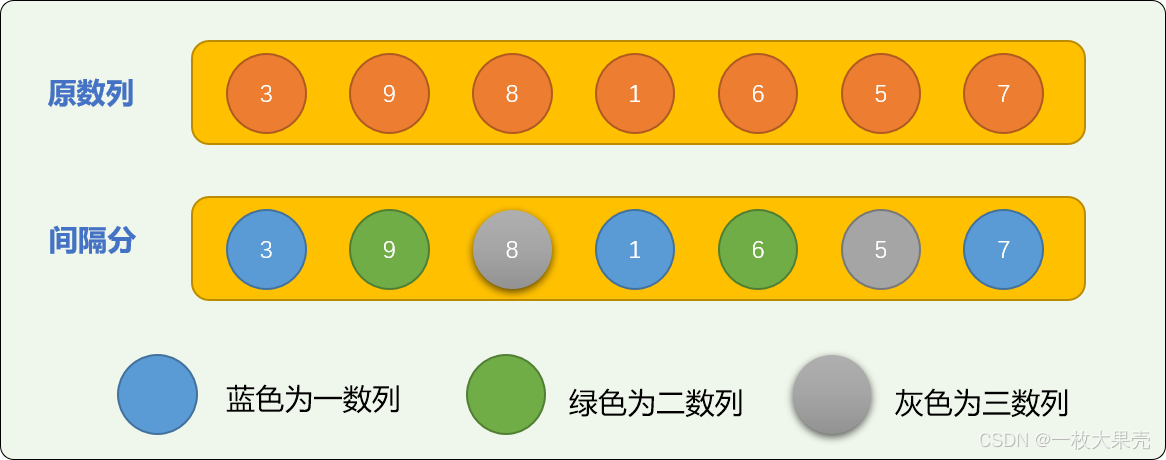
对切分后的 3 个子数列排序后可得到下图：

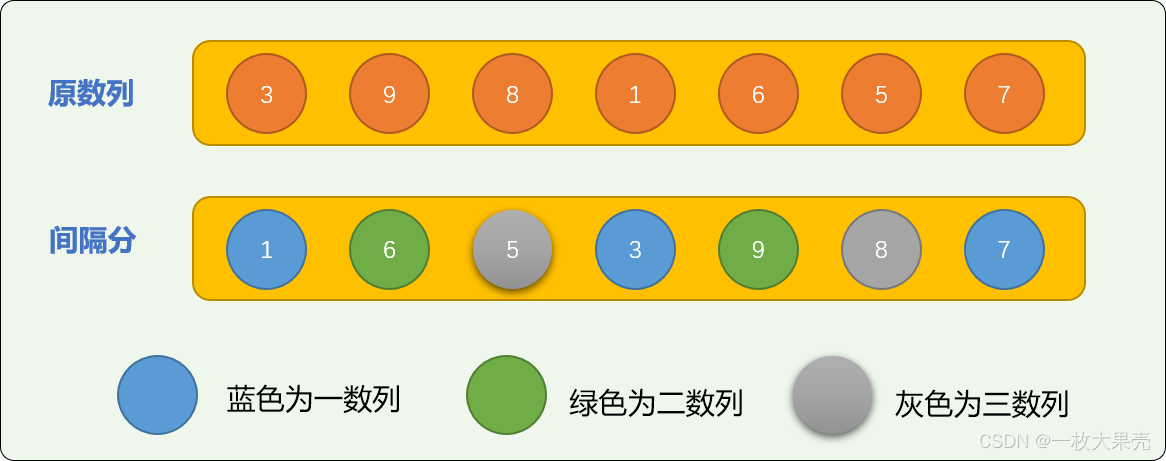
在此基础之上，再进行插入排序的的次数要少很多。

使用增量切分后再排序，原始数列中的数字的位置变化范围较大。

如数字 9 原始位置是 1，经过增量切分再排序后位置可以到 4。已经很接近 9 的最终位置 6 了。

下图是增量切分后数字位置的变化图，可以看出来，几乎所有的数字都产生了位置变化 ，且位置变化的跨度较大。有整体趋于有序的势头。

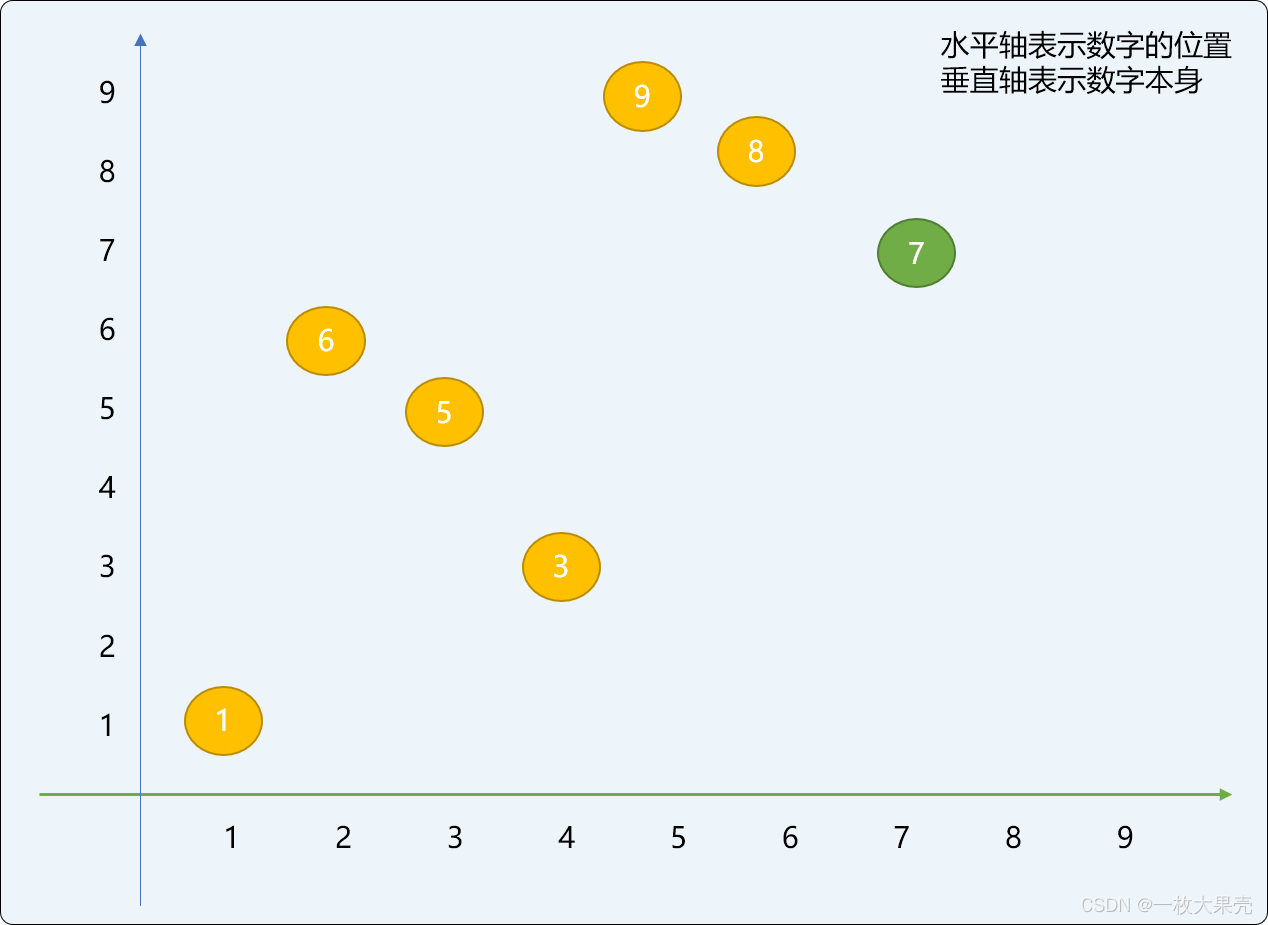
实现希尔排序算法时，最佳的方案是先初始化一个增量值，切分排序后再减少增量值，如此反复直到增量值等于 1 （也就是对原数列整体做插入排序）。

增量值大，数字位置变化的跨度就大，增量值小，数字位置的变化会收紧。

编码代码希尔排序：

# 希尔排序
def shell_sort(nums):
    # 增量
    increment = len(nums) // 2
    # 新数列
    while increment > 0:
        # 增量值是多少，则切分的子数列就有多少
        for start in range(increment):
            insert_sort(nums, start, increment)
        # 修改增量值，直到增量值为 1    
        increment = increment // 2
        
# 插入排序
def insert_sort(nums, start, increment):
    for back_idx in range(start + increment, len(nums), increment):
        for front_idx in range(back_idx, 0, -increment):
            if nums[front_idx] < nums[front_idx - increment]:
                nums[front_idx], nums[front_idx - increment] = nums[front_idx - increment], nums[front_idx]
            else:
                break

nums = [3, 9, 8, 1, 6, 5, 7]
shell_sort(nums)
print(nums)

这里会有一个让人疑惑的观点：难道一次插入排序的时间复杂度会高于多次插入排序时间复杂度？

通过切分方案，经过子数列的微排序（因子数列数字不多，其移动交换量也不会很大），最后一次插入排序的移动次数可以达到最小，只要增量选择合适，时间复杂度可以控制 在 O(n) 到 O（<sup>2</sup>） 之间。完全是有可能优于单纯的使用一次插入排序。

3. 归并排序

归并排序算法也是基于分治思想。和希尔排序一样，需要对原始数列进行切分，但是切分的方案不一样。

相比较希尔排序，归并排序的分解子问题，求解子问题，合并子问题的过程分界线非常清晰。可以说，归并排序更能完美诠释什么是分治思想。

3.1 分解子问题

归并排序算法的分解过程采用二分方案。

• 把原始数列一分为二。

• 然后在已经切分后的子数列上又进行二分。

• 如此反复，直到子数列不能再分为止。

  如下图所示：

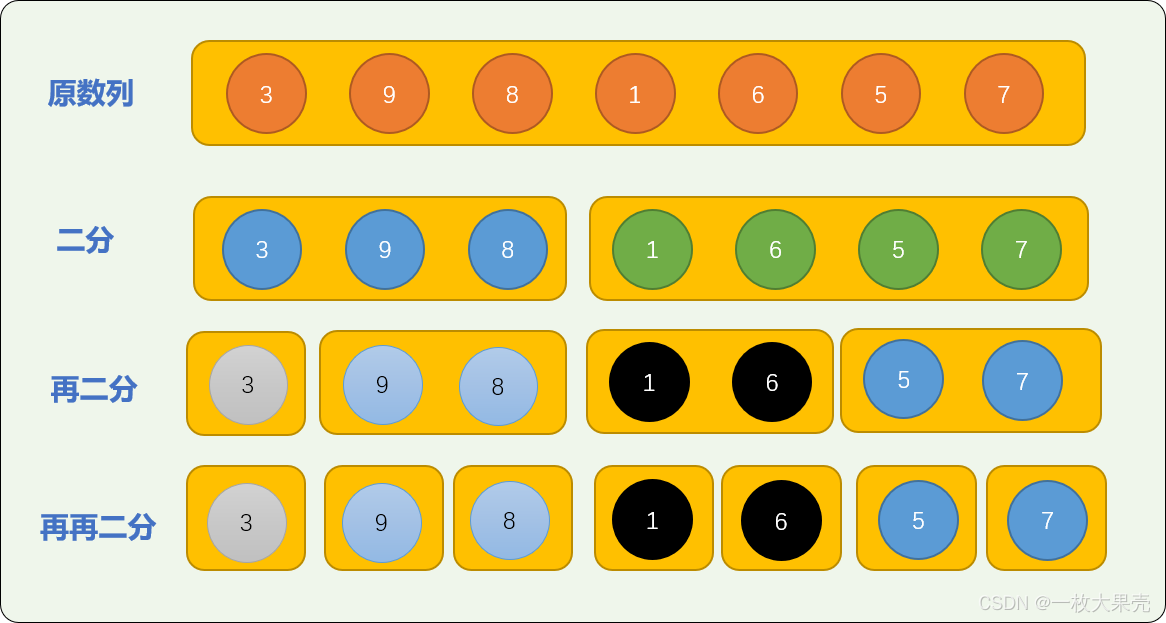
如下代码，使用递归算法对原数列进行切分，通过输出结果观察切分过程：

# 切分原数列
def split_nums(nums):
    print(nums)
    if len(nums) > 1:
        # 切分线，中间位置
        sp_line = len(nums) // 2
        split_nums(nums[0:sp_line])
        split_nums(nums[sp_line:])

nums = [3, 9, 8, 1, 6, 5, 7]
split_nums(nums)

输出结果：和上面演示图的结论一样。

[3, 9, 8, 1, 6, 5, 7]
[3, 9, 8]
[3]
[9, 8]
[9]
[8]
[1, 6, 5, 7]
[1, 6]
[1]
[6]
[5, 7]
[5]
[7]

3.2 求解子问题

切分后，对每相邻 2 个子数列进行合并。当对相邻 2 个数列进行合并时，不是简单合并，需要保证合并后的数字是排序的。如下图所示：

3.3 合并排序

如何实现 2 个数字合并后数字有序？

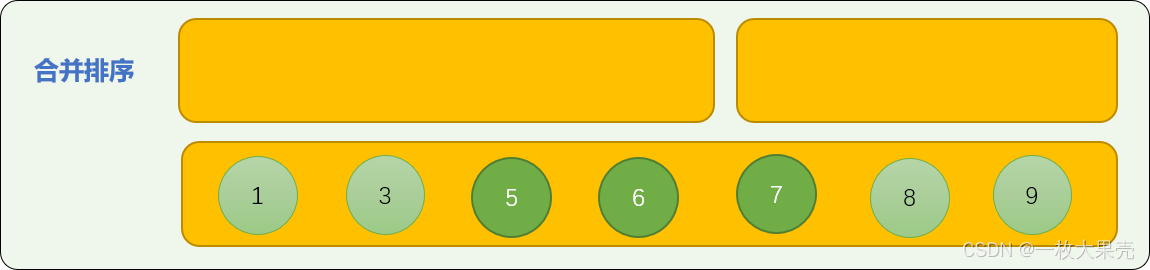
使用子数列中首数字比较算法进行合并排序。如下图演示了如何合并 nums01=[1,3,8,9]、nums02=[5,6,7] 2 个子数列。

子数列必须是有序的！！

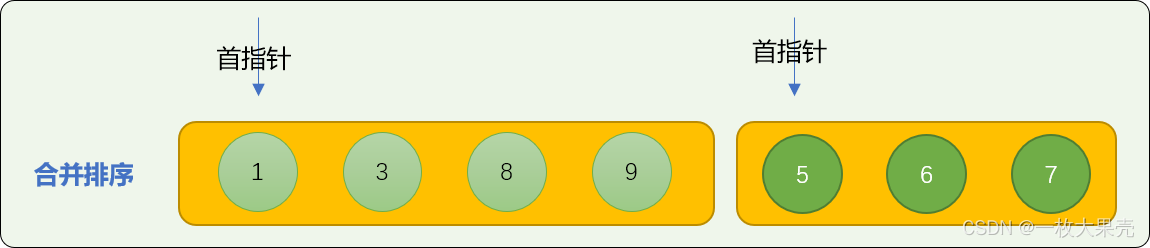
• 数字 1 和 数字 5 比较，5 大于 1 ，数字 1 先位于合并数列中。

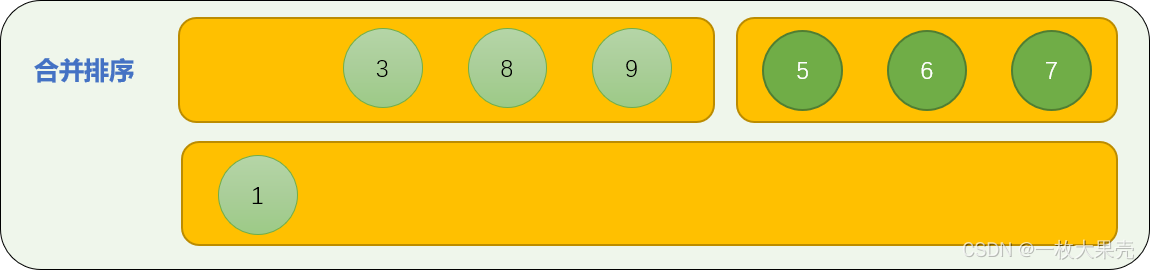
• 数字 3 与数字 5 比较，数字 3 先进入合并数列中。

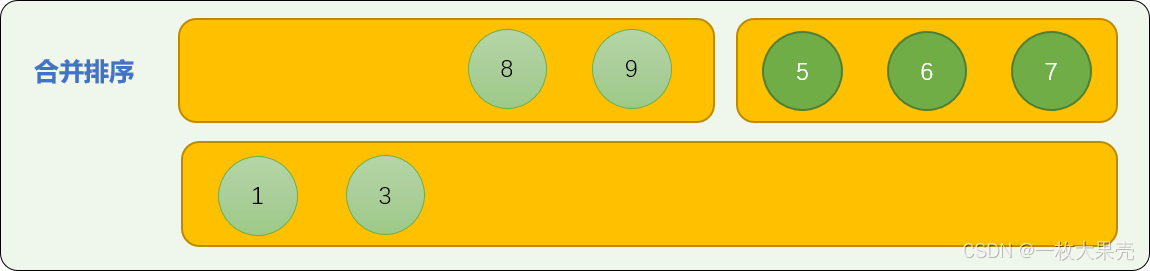
• 数字 8 和数字 5 比较，数字 5 进入合并数列中。

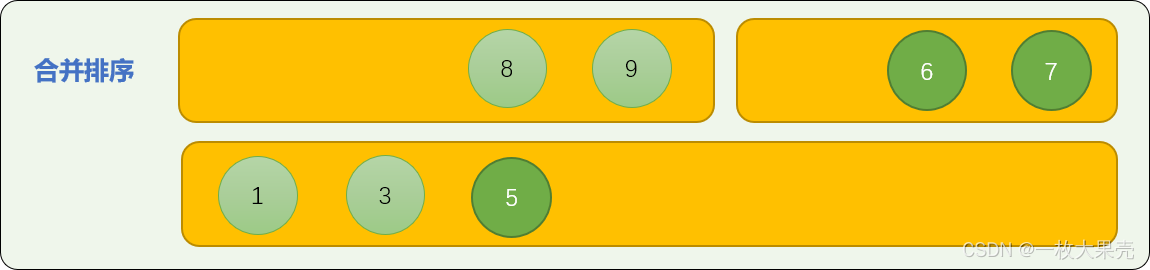
从头至尾，进行首数字大小比较，最后，可以保证合并后的数列是有序的。

编写一个合并排序代码：

如果仅仅是合并 2 个有序数列，本文提供 2 个方案：

• 不增加额外的存储空间：把最终合并排序好的数字全部存储到其中的一个数列中。

def merge_sort(nums01, nums02):
    # 为 2 个数列创建 2 个指针
    idx_01 = 0
    idx_02 = 0
    while idx_01 < len(nums01) and idx_02 < len(nums02):
        if nums01[idx_01] > nums02[idx_02]:
            # 这里不额外增加存储空间，如果数列 2 中的值大于数字 1 的插入到数列 1 中
            nums01.insert(idx_01, nums02[idx_02])
            idx_02 += 1
        # 数列 1 的指针向右移动    
        idx_01 += 1
    # 检查 nums02 中的数字是否已经全部合并到 nums01 中
    while idx_02 < len(nums02):
        nums01.append(nums02[idx_02])
        idx_02 += 1

nums01 = [1, 2, 8, 9]
nums02 = [5, 6, 7, 12, 15]
merge_sort(nums01, nums02)
# 合并后的数字都存储到了第一个数列中
print(nums01)
'''
输出结果：
[1,2,5,6,7,8,9,12,15]
'''

• 增加一个空数列，用来保存最终合并的数字。

# 使用附加数列
nums=[]
def merge_sort(nums01, nums02):
    # 为 2 个数列创建 2 个指针
    idx_01 = 0
    idx_02 = 0
    k=0
    while idx_01 < len(nums01) and idx_02 < len(nums02):
        if nums01[idx_01] > nums02[idx_02]:
            nums.append(nums02[idx_02])
            idx_02 += 1
        else:
            nums.append(nums01[idx_01])
            idx_01 += 1
        k+=1
    # 检查是否全部合并
    while idx_02 < len(nums02):
        nums.append(nums02[idx_02])
        idx_02 += 1
    while idx_01 < len(nums01):
        nums.append(nums01[idx_01])
        idx_01 += 1

nums01 = [1, 2, 8, 9]
nums02 = [5, 6, 7, 12, 15]
merge_sort(nums01, nums02)
print(nums)

前面是分步讲解切分和合并逻辑，现在把切分和合并逻辑合二为一，就完成了归并算法的实现：

def merge_sort(nums):
    if len(nums) > 1:
        # 切分线，中间位置
        sp_line = len(nums) // 2
        nums01 = nums[:sp_line]
        nums02 = nums[sp_line:]
        merge_sort(nums01)
        merge_sort(nums02)

        # 为 2 个数列创建 2 个指针
        idx_01 = 0
        idx_02 = 0
        k = 0
        while idx_01 < len(nums01) and idx_02 < len(nums02):
            if nums01[idx_01] > nums02[idx_02]:
                # 合并后的数字要保存到原数列中
                nums[k] = nums02[idx_02]
                idx_02 += 1
            else:
                nums[k] = nums01[idx_01]
                idx_01 += 1
            k += 1
        # 检查是否全部合并
        while idx_02 < len(nums02):
            nums[k] = nums02[idx_02]
            idx_02 += 1
            k += 1
        while idx_01 < len(nums01):
            nums[k] = nums01[idx_01]
            idx_01 += 1
            k += 1

nums = [3, 9, 8, 1, 6, 5, 7]
merge_sort(nums)
print(nums)

个人觉得，归并算法对于理解分治思想有大的帮助。

从归并算法上可以完整的体现分治理念的哲学之美。

4. 基数排序

基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或 bin sort。

基数排序没有使用分治理念，放在本文一起讲解，是因为基数排序有一个对数字自身切分逻辑。

基数排序的最基本思想：

如对原始数列 nums = [3, 9, 8, 1, 6, 5, 7] 中的数字使用基数排序。

• 先提供一个长度为 10 的新空数列（本文也称为排序数列）。

  为什么新空数列的长度要设置为 10？等排序完毕，相信大家就能找到答案。

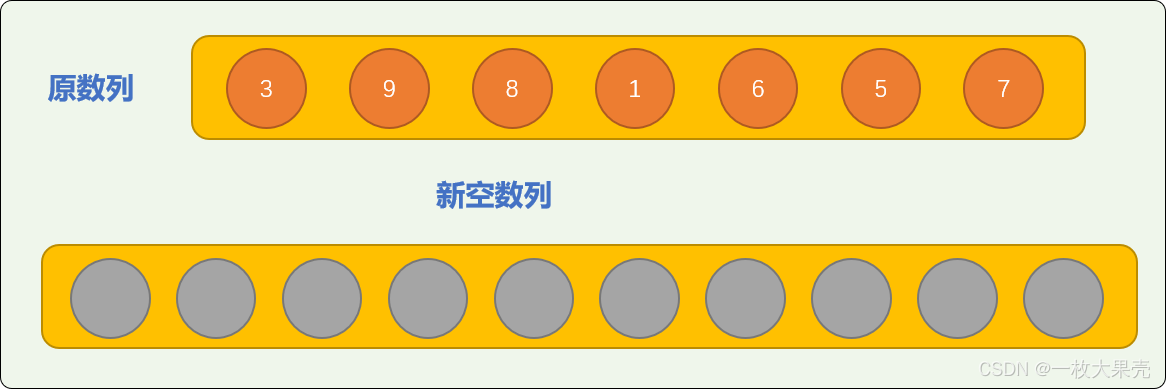
。把原数列中的数字转存到新空数列中，转存方案：

nums 中的数字 3 存储在新数列索引号为 3 的位置。

nums 中的数字 9 存储在新数列索引号为 9 的位置。

nums 中的数字 8 存储在新数列索引号为 8 的位置。

……

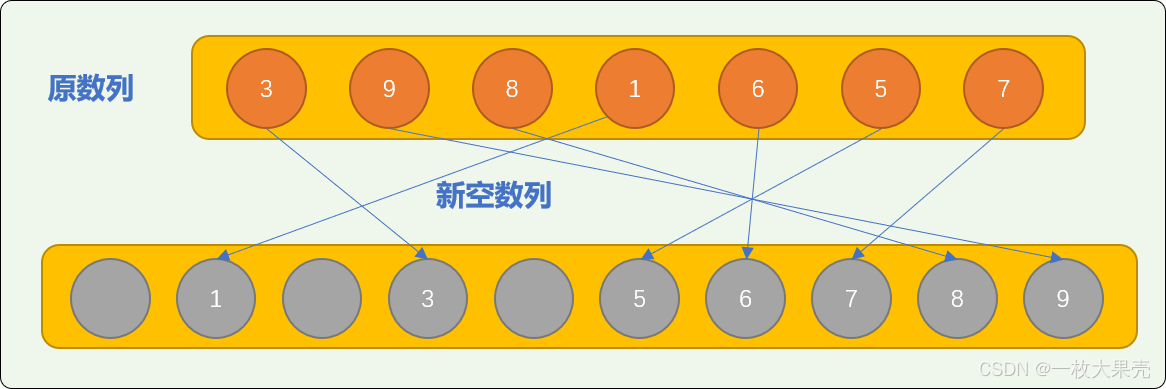
从上图可知，原数列中的数字所转存到排序数列中的位置，是数字所代表的索引号所指的位置。显然，经过转存后，新数列就是一个排好序的数列。

新空数列的长度定义为多大由原始数列中数字的最大值来决定。

编码实现：

# 原数列
nums = [3, 9, 8, 1, 6, 5, 7]
# 找到数列中的最大值
sort_nums=[0]*(max(nums)+1)
for i in nums:
    sort_nums[i]=i

print([i for i in sort_nums if i!=0])
'''
输出结果：
[1,3,5,6,7,8,9]
'''

使用上述方案创建新空数据，如果数字之间的间隔较大时，新数列的空间浪费就非常大。

如对 nums=[1,98,51,2,32,4,99,13,45] 使用上述方案排序，新空数列的长度要达到 99 ，真正需要保存的数字只有 7 个，如此空间浪费几乎是令人恐怖的。

所以，有必要使用改良方案。如果在需要排序的数字中出现了 2 位以上的数字，则使用如下法则：

• 先根据每一个数字个位上的数字进行存储。个位数是 1 存储在位置为 1 的位置，是 9 就存储在位置是 9 的位置。如下图：

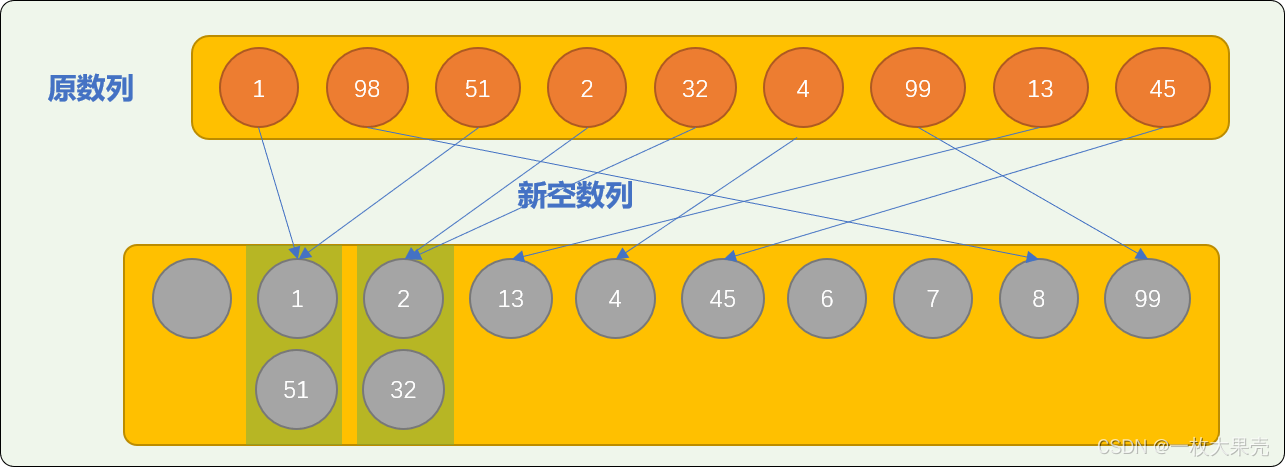
可看到有可能在同一个位置保存多个数字。这也是基数排序也称为桶排序的原因。

一个位置就是一个桶，可以存放多个具有相同性质的数字。如上图：个位上数字相同的数字就在一个桶中。

• 把存放在排序数列中的数字按顺序重新拿出来，这时的数列顺序变成 nums=[1，51，2，32，13，4，45，8，99]
• 把重组后数列中的数字按十位上的数字重新存入排序数列。

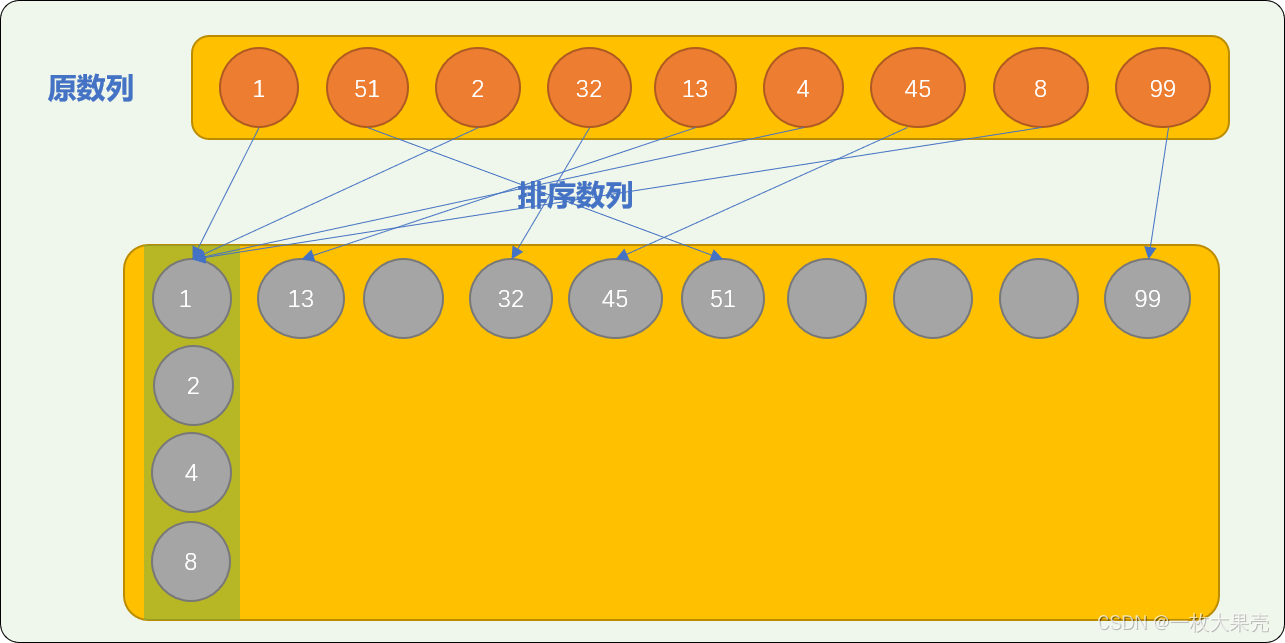
可以看到，经过 2 轮转存后，原数列就已经排好序。

这个道理是很好理解的：

现实生活中，我们在比较 2 个数字 大小时，可以先从个位上的数字相比较，然后再对十位上的数字比较。

基数排序，很有生活的味道！！

编码实现基数排序：

nums = [1, 98, 51, 2, 32, 4, 99, 13, 45]
# 数列中的最大值
m = max(nums)
# 确定最大位数，用来确定需要转存多少次
l = len(str(m))

for i in range(l + 1):
    # 排序数列，也是桶
    sort_nums = [[] for _ in range(10)]
    for n in nums:
        # 分解数字个位上的数字
        g_s = (n // 10 ** i) % 10
        # 根据个位上的数字找到转存位置
        sub_nums = sort_nums[g_s]
        sub_nums.append(n)
    # 合并数据
    nums = []
    for l in sort_nums:
        nums.extend(l)
print(nums)
'''
输出结果：
[1, 2, 4, 13, 32, 45, 51, 98, 99]
'''

上述转存过程是由低位到高位，也称为 LSD ，也可以先高位后低位方案转存MSD。

5. 总结

分治很有哲学味道，当你遇到困难，应该试着找到问题的薄弱点，然后一点点地突破。

当遇到困难时，老师们总会这么劝解我们。

分治其实和项目开发中的组件设计思想也具有同工异曲之处。