摘要本文记录阅读该paper的笔记,这篇论文是TenSeal库的原理介绍。
机器学习算法已经取得了显著的效果,并被广泛应用于各个领域。这些算法通常依赖于敏感和私有数据,如医疗和财务记录。因此,进一步关注隐私威胁和应用于机器学习模型的相应防御技术至关重要。在本文中,我们介绍了TenSEAL,这是一个使用同态加密保护隐私数据的机器学习开源库,可以轻松地集成到流行的机器学习框架(PyTorch 或 Tensorflow)中。我们使用MNIST数据集对我们的实现进行了benchmark测试,结果显示加密的卷积神经网络可以在不到一秒钟的时间内进行计算,通信量不到1/2MB。
介绍近年来,机器学习狂奔发展。在典型场景中,用户需要将数据发送给服务提供商,服务提供商将对数据执行一些计算并返回结果。
这种方法有两个关键问题。首先,出于隐私考虑,用户可能不想将其数据发送给服务提供商。其次,如果用户不向服务提供商发送数据,那服务提供商就无法向用户提供模型。使用同态加密,可以解决该问题,用户的数据将始终加密,服务提供商将看不到输入和输出,并且仍然可以对这些加密数据进行计算。
然而,在机器学习中采用同态加密的速度很慢。问题一:虽然目前可用的密码库为密码学家提供了一个优秀的API,但它们可能会对数据科学家使用就不方便了(触及密码专业知识)。问题二:是计算成本,包括通信和计算成本。
本文工作提供了一个灵活的开源库,使用同态加密进行张量计算(tensor computation)。该库可以直接将当前流行机器学习框架(如PyTorch或Tensorflow)中的张量转换为加密所支持的明文形式。
对于本文的其余部分,第2节中描述该库的体系结构。然后在第3节,详细介绍了在加密空间中计算卷积神经网络所需的算法。在第5节中对我们的库进行了实验性测试,并在第6节总结了我们工作的一些局限性。
文章结构TenSEAL是一个连接经典机器学习框架和同态加密功能的库。它实现了在加密数据上进行张量计算。TenSEAL依赖于Microsoft SEAL库。客户端可以计算明文或加密的张量(支持C++或Python)。在客户机-服务器场景中,消息交换是使用协议缓冲区完成的。核心API主要组件构建:环境(context)、明文张量(PlainTensor)和密文张量(Encrypted Tensor)计算。
环境(context)TenSEAL的context是库的核心组件,它生成并存储密钥(用于解密的私钥、用于加密的公钥、用于旋转的伽罗瓦密钥以及用于密文重新线性化的重新线性化密钥)。这个对象还将处理线程池,线程池控制在执行可并行化操作时应并行运行的作业数。另外在context中可以设置自动密文重新线性化(relinearization)和重新缩放(rescaling )。
明文张量(PlainTensor) 张量(Tensor)Tensor是深度学习中广泛使用的数据结构,本质上就是一个高维的矩阵,甚至将其理解为NumPy中array,Pandas中的DataFrame。
单个元素叫标量(scalar),一个序列叫向量(vector),多个序列组成的平面叫矩阵(matrix),多个平面组成的立方体叫张量(tensor)。在深度学习的范畴内,标量、向量和矩阵都统称为张量。
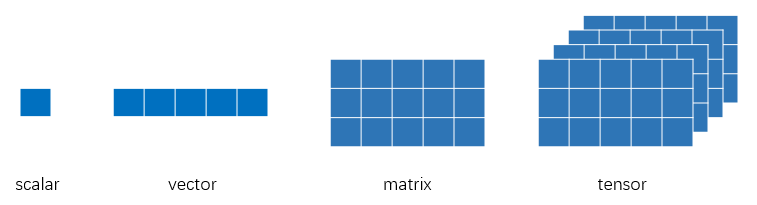
参考:
1、PyTorch学习系列教程:何为Tensor?

该图显示了密文张量的构建,PlainTensor封装了当前流行框架中的张量表示,并用EncryptedTensor接口的输入。
PlainTensor是一个将未加密的张量连接到加密实现的类。
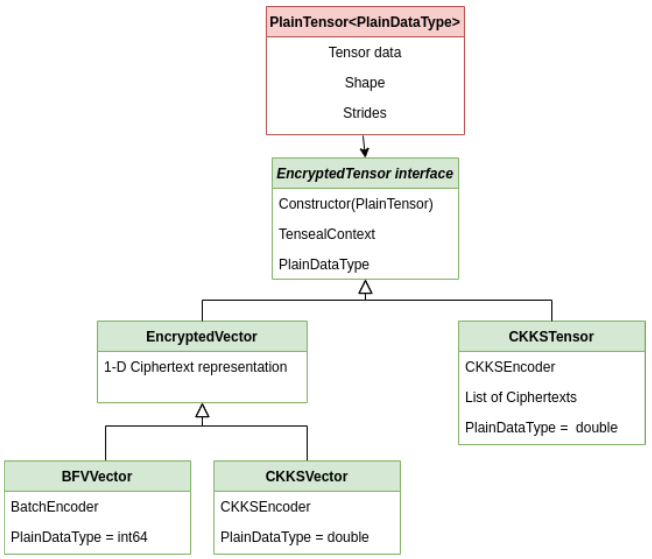
这显示了张量的关系。EncryptedTensor接口派生为BFVVector、CKKVector或CKKSTensor类。
EncryptedSensor接口提供了一个API,该API需要由库公开的每个张量来实现。接口有一个TenSEALContext对象,这是进行任何同态计算所必需的。派生类公开了不同的张量风格,例如:
- CKKSVector派生EncryptedVector接口,可以将实数向量加密为单个密文。
- CKKSTensor将的N维实数张量加密为的N维密文张量。然而,在对密文批处理时,需要一个轴(axis),因此只需要(N-1)维密文张量。
在同态加密方案上构建张量时,需要解决两个重要问题:
1,如何在加密之前对张量进行编码?
2、使用特定编码时可以执行哪些操作?
CKKS方案的批处理功能允许将N×N矩阵加密为N维密文向量,每行或每列作为一个密文。另一种可能性是将整个张量(N×N矩阵)加密为一个密文【paper:Secure outsourced matrix compu- tation and application to neural networks】。根据我们如何将明文张量放入密文中,我们可以用执行不同的操作(不同的复杂度)。目标是使用最小数量的密文,并以最小的运行时间获得最大的深度,从而优化内存和计算。为了实现这一理想目标,我们发现可以将输入图像进行加密为单个密文,并在卷积神经网络上对其进行计算。这需要客户端上的预处理步骤将图像编码为矩阵,由卷积窗口作为行组成,然后通过垂直扫描将其展平为向量。在TenSEAL中,所有这些功能都是围绕CKKSVector实现的。CKKSVector包含N/2个实数,其中N是模多项式的次数。我们可以使用其他密文或者明文向量执行逐元素计算(加法、减法和乘法)。我们有一种计算加密向量次幂的方法,该方法使用最佳电路,从而使用最小乘法深度。此外,由于我们需要近似计算多项式,对于不同的激活函数,我们构建了一种以加密向量为变量的多项式求值的方法,确保使用最小电路。除了元素操作之外,我们还需要矩阵操作来执行机器学习任务。我们实现了密文向量乘明文矩阵【paper:Algorithms in helib】,它可以使用多线程来更快地运行。下面是该库的密文张量支持的操作:

该库为点积提供计算方法【类似:Algorithms in helib】,但支持的向量大小不是2的幂,或者不能填充密文的所有插槽。前一种方法中的这种限制是由于向右旋转(希望最后一个元素是第一个元素),这对于我们所处理的情况来说是不正确的。如果向量大小不是2的幂,我们的方法仅限于特定数量的点积。然而,由于方案允许的乘法次数可能较低,因此通常无法达到此限制。所以通过尽可能多次将输入向量复制到密文槽中,并且在计算过程中只有密文左旋转,该方法和【Algorithms in helib】有相同的算法复杂性。我们使用【CKKS17】中的方法实现了密文向量与明文矩阵之间的点积。因此,它可以扩展到支持密文矩阵与明文矩阵之间的点积(矩阵乘法)。下图显示了如何在加密向量和普通矩阵之间执行点积:
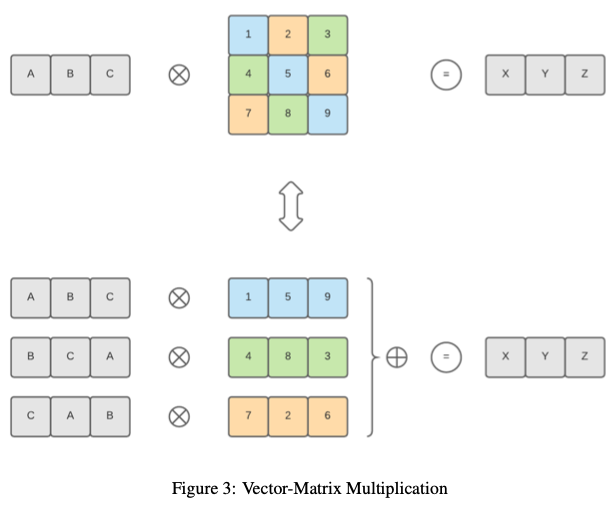
卷积是一种数学运算,对两个函数(信号)的乘积进行积分,其中一个信号翻转。
下面我们将两个信号卷积\(x =(0,1,2,3,4),w =(1,-1,2)\):
(1)首先是将W水平翻转(或向左旋转180度)
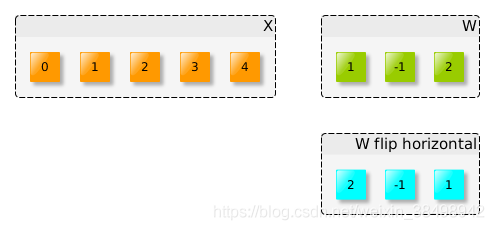
(2)需要将翻转的W滑过输入X:
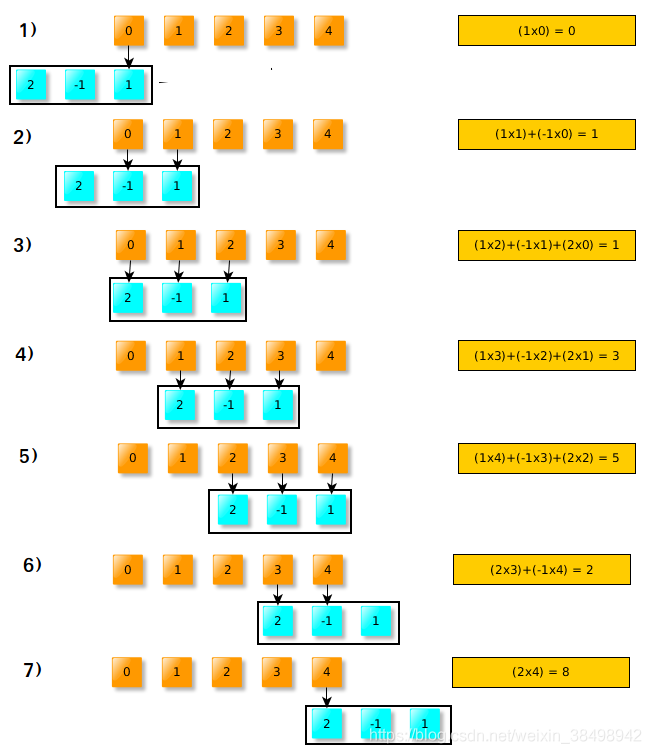
其中,在步骤3、4、5上,翻转的窗口完全位于输入信号内。 这些结果称为“有效”卷积。 如果翻转的窗口未完全位于输入窗口(X)内,则可以考虑为零,或计算可能计算出的值,例如 在第1步中,我们将1乘以零,其余的将被忽略。
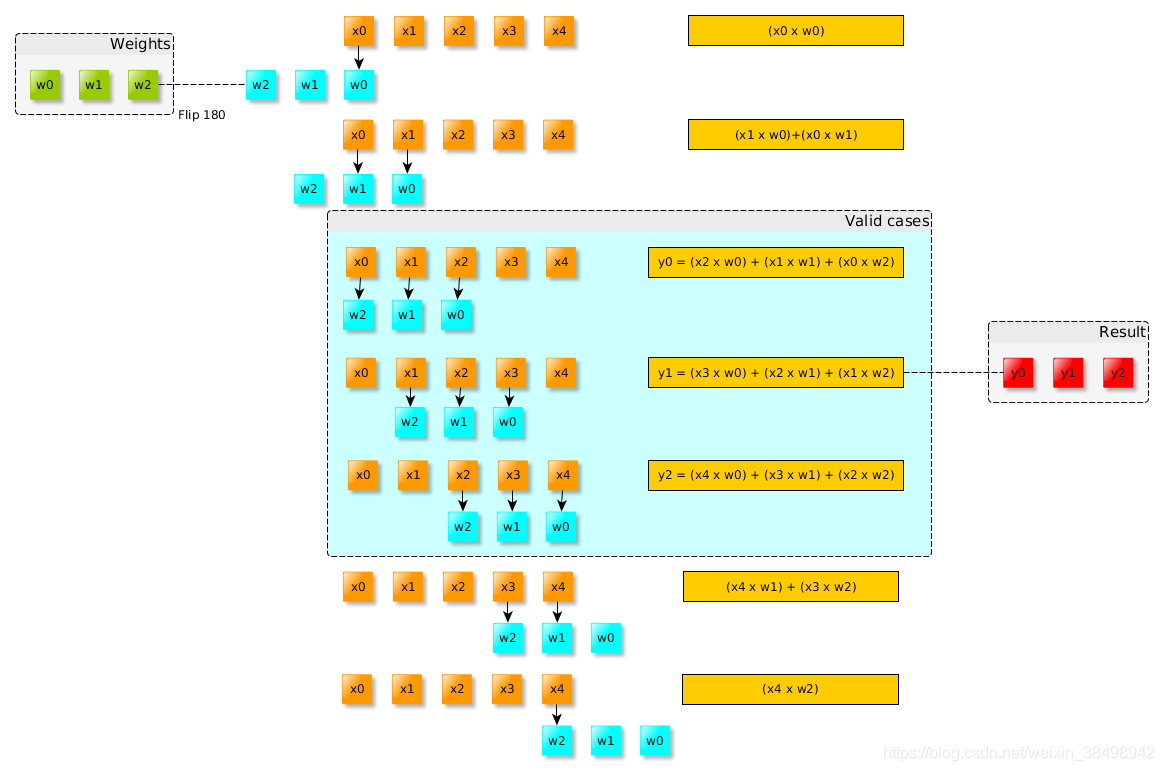
参考:
1、深度 | 理解深度学习中的卷积
二维卷积可以使用单个矩阵乘法来执行,而不是在每个窗口上重复乘法。这种方法称为图像块到列的卷积( image block to column),或图像到列的卷积(image to column)。下图显示了如何使用此方法执行卷积。它首先将输入矩阵重新组织成表示卷积窗口的行,然后用flattened kernel执行点积。
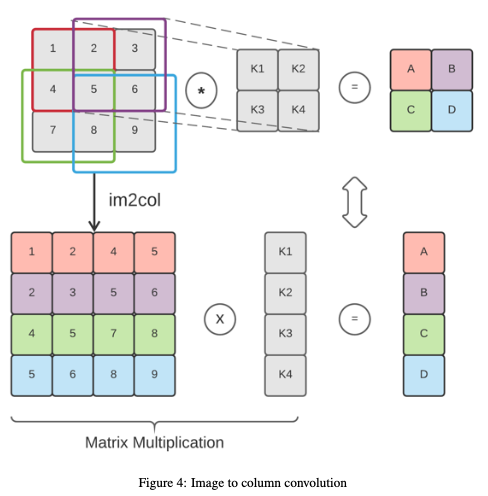
将此技术应用于加密矩阵(加密为一个密文)并不是一件小事,因为重新组织slot并不简单。我们需要在加密之前将矩阵重新组织为预处理步骤,以便为卷积做好准备。明文向量(kernel)和密文矩阵(输入图像)的计算可以通过逐元素乘法和一系列旋转和累加来执行。下图显示了执行此操作的步骤。第一个显示了密文矩阵(彩色)是如何编码并与明文向量(kernel)相乘的。第二步是对向左旋转不同的不同版本的输出求和。
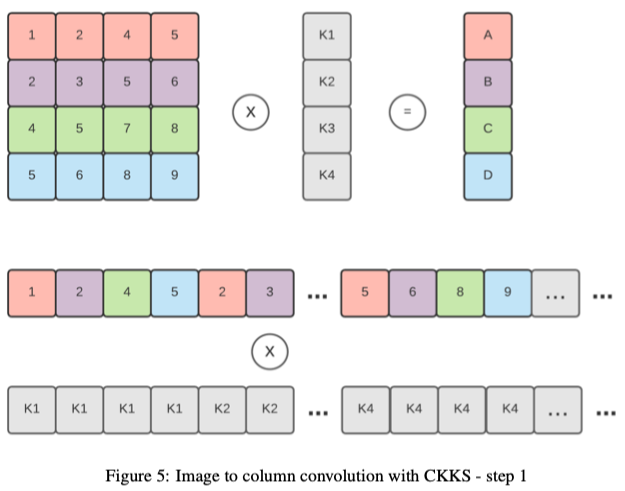
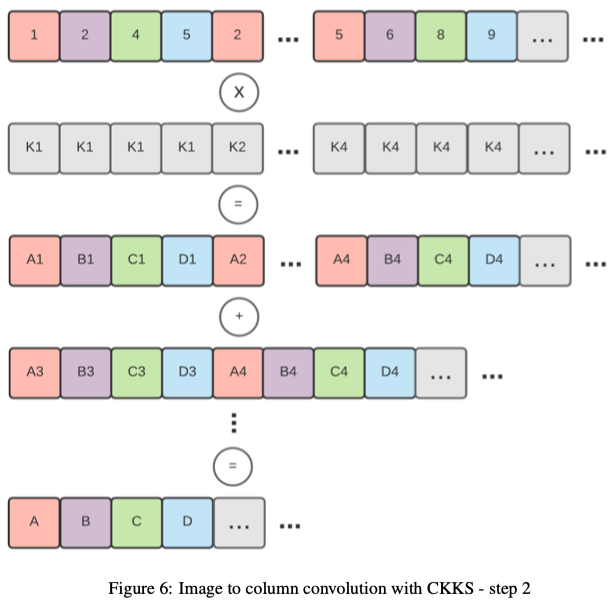
TenSEAL还支持计算卷积,即提供当前流行的机器学习框架(例如PyTorch)计算卷积的类似实现。我们将图像块应用于Columns (im2col)【paper:Cnns in practice】,将卷积层转换为单个矩阵乘法运算。这种技术需要密文矩阵乘明文向量,我们通过复制的明文向量和转置的矩阵逐元素向乘来实现。最后,将结果旋转并累加到单个密文向量中。
此操作仅使用一个乘法运算和\(log2(N)\)个旋转和加法,其中N表示矩阵中的行数。下面解释了如何将“图像块-》列”算法应用于加密输入。需要注意的是,转换发生在明文数据中,转换后的输入图像进行编码和加密为单个密文。这直接意味着堆叠两个卷积是不可能的,因为重新组织密文的slot并不简单。
相关工作近年来,一些研究工作已经使同态加密方案在机器学习中实用化。【paper:Cryptonets: Applying neural networks to encrypted data with high throughput and accuracy】实现了CryptoNets,一种使用YASHE(一种Leveled-FHE方案)【paper:Improved security for a ring-based fully homomorphic encryption scheme】具有高效的简单加法和乘法算法,适用于对密文数据进行推理的神经网络。然而,该框架需要大批量才能实现良好的摊销性能,这使得它对于计算单个实例不太实用。
【paper:ngraph-he: a graph compiler for deep learning on homomorphically encrypted data】在实现不同的优化层时,使用了类似的张量结构(CryptoNets)。他们对于HE应用程序shying了特别的图形级优化,这减少了乘法深度对于计算操作(比如批处理和平均池(average pooling))。。。。
所有工作都使用MNIST数据集进行benchmarked测试,但硬件配置不同。下表1中总结了相应论文中报告的实证结果。
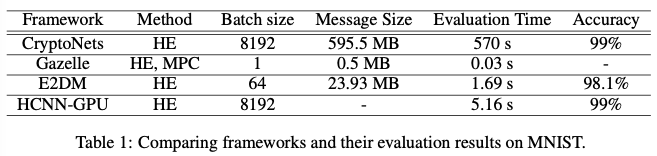
为了测试我们的库和技术,我们实现了一个由以下部分组成的神经网络:卷积层(4个7x7的内核,步长为3x3)、线性层(输入:256,输出:64)和最终线性层(输入:64,输出:10)。除最后一层外,我们在每一层后使用平方激活函数。卷积是使用我们的图像-》列实现完成的,而线性层使用点积实现。明文测试集的准确率为97.7%,而密文测试集的准确率为97.4%。我们使用了CKKSVector实现,它使用CKKS方案。知道我们需要6次乘法计算和128位的安全级别,我们将模多项式的级数(N)设置为8192,系数模数为206位,缩放因子(scale)为21位。测试是在Ubuntu服务器20.04和Python 3.8上使用AWS c4完成的。2xlarge(8个VCPU)和AWS c4。4XL(16个VCPU)配置。测试的持续时间是5轮测试的平均值,每轮10次迭代。下表包含了在从MNIST数据集采样的加密图像上计算神经网络的完整细分。

上表是测试MNIST计算的完整说明,持续时间以毫秒表示。我们使用两种设置来测试这些方法:Amazon c4。2xlarge实例(8个VCPU,15个GiB内存)和Amazon c4。4xlarge实例(16个VCPU,30 GiB内存),强调该库并行性优秀。
结果表明,该库大量实现并行,在网络通信方面具有很强的竞争力,只需427KB的通信即可发送加密的输入和接收加密的输出。同时,TenSEAL没有强行定义批处理的大小(batch size),这使得它非常实用。完整的benchmarks测试是开源的,其结果下面展示。
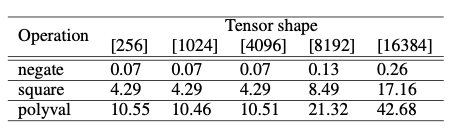
显示了不同算术运算的平均性能。具体来说一元操作的持续时间(毫秒)。CKKS的context是由模多项式的级数8192和系数模数200位创建的。polyval benchmark是针对\(2X^2+X\)执行的。
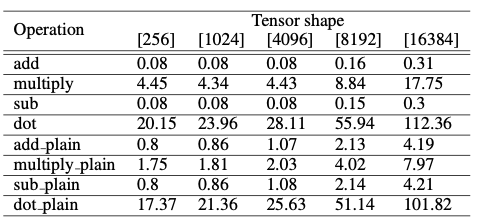
显示了矩阵乘法的平均性能。具体来说,二元操作的持续时间(毫秒)。CKKS的context是由模多项式级数8192和系数模数200位创建的。对于“明文”操作,操作数是shape相同的明文张量。对于其余部分,操作数是shape相同的密文张量。
加密部分依赖于【paper:CKKS17】,这是Leveled-FHE方案。这意味着,根据我们的参数选择,我们可以对密文数据执行的乘法数量是有限的,这直接影响我们可以使用的机器学习模型或其深度。不同的机器学习模型也使用非线性激励函数,在CKKS的情况下,需要使用近似多项式计算)。最近的一项工作【paper:New challenges for fully homomorphic encryption】一直试图通过使用TFHE方案【paper:Tfhe: fast fully homo- morphic encryption over the torus】来解决与机器学习密切相关的这个问题,该方案允许评估更深层次的模型以及非线性激活函数。
最后,我们的结果表明,利用CKKS方案进行张量计算是可行的。根据使用情况,用户可以选择高级张量操作(slicing、broadcasting)或使用更多计算通信优化实现。TenSEAL可以适应这两种情况,同时提供从传统机器学习框架的平稳过渡。最后,我们试图扩展tensor operations catalog,并进一步提高整体性能。
