【js奇妙说】如何跟非计算机从业者解释，为什么浮点数计算0.1+0.2不等于0.3？

壹 ❀ 引

0.1+0.2不等于0.3，即便你不知道原理，但也应该听闻过这个问题，包括博主本人也曾在面试中被问到过此问题。很遗憾，当时只知道一句精度丢失，但是什么原因造成的精度丢失却不太清楚。而我在查阅资料的过程中发现，大部分文章都是假定了你有一定计算机基础，对于非此专业的人来说，可能文章读起来就显得晦涩难懂。那么本文就会站在此问题的角度，从二进制计算说起说起，用基础数学通俗易懂的去解释究竟是什么原因造成了计算机中浮点数计算的精度丢失，本文开始。

贰 ❀ 从二进制说起

与我们人的计算思维不同，计算运算采用二进制而非十进制，毕竟人可以用十根手指表示十个数字。而对于早期计算机而言，第一代电子管数字机（1946年）在硬件方面，逻辑元件采用的都是真空电子管，而使用电子管表示十种状态过于复杂，所以当时的电子计算机只有两种状态，即开和关，因此电子管的两种状态也奠定了计算机采用二进制来表示数字和数据。

十进制非常好理解，比如一个基础的十进制计算：

9 + 2 = 11 // 逢十进一，剩余1个1，所以等同于10 + 1,因此是11

与十进制的逢十进一不同，二进制只有0和1两个数字，它遵循逢二进一，比如：

1 + 1 = 10 //1+1等于2，逢二进一，因此为10，这里读作一零，而不是十

除了加法，二进制一样存在加减乘除的操作，比如：

// 加法
0 + 0 = 0; 0 + 1 = 1; 1 + 0 = 1; 1 + 1 = 10;
// 减法
0 - 0 = 0; 1 - 0 = 1; 1 - 1 = 0; 0 - 1 = 1;
// 乘法
0 * 0 = 0; 1 * 0 = 0; 0 * 1 = 0; 1* 1 = 1;
// 除法
0 / 1 = 0； 1 / 1 = 1;

那么到这里，我们了解了二进制的基本计算规则。而回到文章开头的问题，0.1+0.2的操作对于计算机而言，它一定是将十进制的数字转成二进制之后做的计算，所以要想知道精度如何丢失，我们肯定得先知道十进制数字如何转变成二进制，我们接着聊。

叁 ❀ 十进制如何转二进制

十进制数如何转二进制数，我们可以先知晓一个规则，考虑到十进制数字存在浮点数，我们可以总结为：

整数部分除以2，一直算到结果为0为止，逆序取余；小数部分乘以2，一直算到结果为1为止，顺序取整。

什么意思呢？我们来以5.625为例，将其拆分成整数部分5，以及小数部分0.625并分别套用上面的公式：

//整数/2    取余
5 / 2 = 2   1
2 / 2 = 1   0
1 / 2 = 0   1
// 逆序取余（从下往上），因此是101

//小数乘以1        取整
0.625 * 2 = 1.25  1
0.25 * 2 = 0.5    0
0.5 * 2 = 1       1
// 顺序取整（从上往下），因此也是101
// 综合起来，转二进制为 101.101

因此5.625转二进制结果为101.101。

OK，我们再来试着转换0.1和0.2为二进制，先看0.1：

0.1 * 2 = 0.2  0
0.2 * 2 = 0.4  0
0.4 * 2 = 0.8  0
0.8 * 2 = 1.6  1
0.6 * 2 = 1.2  1
0.2 * 2 = 0.4  0 // 开始陷入循环
0.4 * 2 = 0.8  0
0.8 * 2 = 1.6  1
0.6 * 2 = 1.2  1
0.2 * 2 = 0.4  0 // 开始循环
0.4 * 2 = 0.8  0
//0.000110011001100110011001100110011001100110011001100...

经过转换我们发现，0.1转二进制会陷入0.2 0.4 0.8 0.6这四个数字的循环，所以最终的结果是一个无限的0.0 0011 0011 0011...的结构。

接着看0.2的二进制转换：

0.2 * 2 = 0.4  0
0.4 * 2 = 0.8  0
0.8 * 2 = 1.6  1
0.6 * 2 = 1.2  1
0.2 * 2 = 0.4  0 // 开始循环
0.4 * 2 = 0.8  0
0.8 * 2 = 1.6  1
0.6 * 2 = 1.2  1
0.2 * 2 = 0.4  0 // 继续循环
0.4 * 2 = 0.8  0
// 0.0011001100110011001100110011001100110011001100110011001...

好家伙，0.2更直接，直接陷入0.2 0.4 0.8 0.6这四个数字的计算循环，因此它转成二进制也是一个无限的0.0011 0011 0011...类型结构的数字。

叁 ❀ 二进制的指数形式

我们知道，计算机的存储空间一定是有限的，即便数字的占用空间再小，它也没办法存储一个无限大的数，那计算机是怎么做的呢？这里就得引入二进制的指数以及浮点数IEEE 745标准两个概念，我们先说二进制的指数。

十进制的指数很好理解，比如数字1000用指数表示为1 * 10^3，其中10为底数，3为指数，翻译过来就是1 * (10 * 10 * 10)，而这个过程其实可以理解成将小数点往左移动了3位；同理，那自然也有也有将小数点往右移，让指数为负数的情况，比如：

1000  1*10^3
0.001 1*10^-3

而二进制的指数与十进制并无区别，只是将指数从10变成了2，一样如果小数点往左移动N位，那么就是2^n，反之往右移动那就是2*-n，看两个简单的例子：

// 这里都是二进制的数字
1010  1.010 * 2^11 // 底数为2，指数为3
0.001 1 * 2^-11    // 底数为2，指数为-3

这里有同学可能就要说了，不是移动3位吗，怎么指数是11，前面已经说了，二进制中只存在数字0和1，数字3转成二进制不就是11了，大家只要心里清楚这里是3即可。

那么说了这么多，指数有什么价值呢？前面也说了计算机内存有限，在有限的空间去尽量描述无限大或者无限小的数字是很有必要的，那么大家可以想想数字10000和数字1*10^4谁更节省空间，以及数字999999和9.99999*10^999999在同等空间下，谁能描述更大的数字，很显然指数更胜一筹，那么到这里我们解释了指数的意义以及二进制指数的描述方式。

肆 ❀ 浮点数的IEEE 754标准

在解释完指数，我们了解到指数能描述和存储更大的数字，但即便再大计算机也没办法使用指数后就能存一个无限长的数字，比如上文十进制0.1转成二进制之后的结果。因此有了指数还不够，计算机还是得对数字做取舍，怎么取舍呢？这就得介绍浮点数的IEEE 754标准了，标准如下：

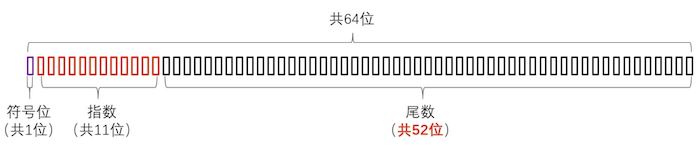
其中符号位占一位，表示这个数字是正数或者负数，如果是正数，符号位是0，反之是负数，那么符号位就是1。

指数部分11位，前面已经解释过指数，比如1*10^11，这里的指数代表的就是11。

尾数部分占52位，比如0.11001100，这里的尾数部分指的就是11001100这一部分。

其实说完尾数，大家应该就知道0.1以及0.2转成二进制的无限小数已经得按尾数的占位规则进行取舍了，这里我们再附上转换之后的二进制数：

// 0.1的二进制
0.000110011001100110011001100110011001100110011001100110011001100110011...
// 0.2的二进制
0.00110011001100110011001100110011001100110011001100110011001100110011...

然后我们再将其转换成二进制指数形式：

// 0.1 二进制指数形式，往右移动4位，指数为-4
1.10011001100110011001100110011001100110011001100110011001100110011... // 指数为-4
// 0.2 二进制指数形式，往右移动3位，指数为-3
1.10011001100110011001100110011001100110011001100110011001100110011... // 指数为-3

前文说了，尾数部分只能是52位，因此我们得做取舍，与十进制四舍五入不同，二进制遵循零舍一入的规则，开始转换：

// 0.1 IEE 754
// 53位是1，进一位
1.10011001100110011001100110011001100110011001100110011
// 52位变成了2，逢二进一
1.1001100110011001100110011001100110011001100110011002
// 最终结果
1.1001100110011001100110011001100110011001100110011010 // 指数为-4

上述转换中，因为53位是1，遵循零舍一入，导致52位变成了2，而二进制逢二进一，因此结尾变成了10。

同理我们也对0.2的二进制指数也做尾数取舍：

// 0.1 IEE 754
// 53位也是1
1.10011001100110011001100110011001100110011001100110011
// 零舍一入后再逢二进一
1.1001100110011001100110011001100110011001100110011010 // 指数为-3

转换完成之后我们需要对两个数求和，但因为指数不同不能直接计算，因此我们将0.1的指数也变成-3：

// 0.1 指数为-3
0.1100110011001100110011001100110011001100110011001101

由于尾数只能有52位，小数点往右移动了一位，因此我们得再舍弃一位，正好最后一位是0，直接舍弃，所以有了上面的结果。

最后我们对如下两个指数相同的数进行求和：

// 0.1 指数为-3
0.1100110011001100110011001100110011001100110011001101
// 0.2 指数为-3
1.1001100110011001100110011001100110011001100110011010
// 指数为-3的和
10.0110011001100110011001100110011001100110011001100111
// 指数为0的和，尾数只能是52位，再次取舍
0.0100110011001100110011001100110011001100110011001101

求和同样是相同位进行加法计算，遵循逢二进一，这里直接给出结果后，再得出指数为0的结果，由于尾数只能是52位，所以我们再次取舍。

在拿到结果后，我们得将二进制再还原成十进制，转换规则为：

位权展开求和，以小数点为起始位，小数点每往左移动n位，当前位结果为当前数字 * 2^n，小数点往右移动一位，当前位结果为当前数字 * 2^-n

由于上述数字整数部分是0，我们不做考虑，那么最终结果应该为：

0*2^-1 + 1*2^-2 + 0*2^-3 + 0*2^-4 + .... + 1*2^-52 

这里我们通过程序来计算这个过程：

const s = '0100110011001100110011001100110011001100110011001101';
let ans = 0;
for (let i = 0; i < s.length; i++) {
  ans += (+s[i]) * Math.pow(2, -(i + 1));
};
console.log(ans); // 0.30000000000000004

如上，我们最终转换的结果为0.30000000000000004，这与控制台输出结果完全一致：

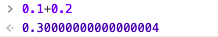
那么到这里，我们解释了为什么0.1+0.2不等于0.3，其本质原因是0.1 0.2在转二进制时因为是无限长小数，为符合IEEE 754标准进行长度取舍以及零舍一入所造成的精度丢失。

伍 ❀ 如何判断0.1+0.2等于0.3

我们可以借用Number.EPSILON来做比较，Number.EPSILON表示1与Number可表示的大于1的最小浮点数之间的差值，比如：

console.log( Math.abs(0.1 + 0.2 - 0.3) <= Number.EPSILON);// true

同理，0.1+0.7其实也不等于0.8，我们一样可以用这种方式做对比：

console.log( Math.abs(0.1 + 0.7 - 0.8) <= Number.EPSILON);

陆 ❀ 总

那么到这里，我们解释了0.1加0.2不等于0.3的本质原因，除此之外，我们也了解二进制与十进制相互转换的规则，以及IEEE 754对于浮点数计算造成的影响。而事实上，并不是所有的浮点数计算都有精度丢失，比如0.5 + 0.5等于1；1/3结果是0.33333...，而当1/3+1/3+1/3时，结果并不是0.999999..而是整数1。当然，在实际开发中当遇到浮点数计算时，我们往往可以将乘以1000或者更大的数之后再进行计算后再还原，尽可能保证其精度的准确性，那么关于0.1与0.2求和的故事就说到这里了，本文结束。