并查集

并查集是一种多叉树，用于处理一些不相交集合的合并与查询问题。

初始化

每个结点单独作为一个集合。

查询

求元素所在集合的代表元素，即根结点。

合并

将两个元素所在的集合合并为一个集合。

合并之前，应先判断两个元素是否属于同一集合，用上面的查询来实现。

实现流程

动态集合中每一个元素由一个对象来表示，设x表示一个对象，并查集的实现需要如下操作：

MAKE(X)

建立一个新的集合，由于各集合是分离的，要求x没有在其他集合中出现过。

UNION(X,Y)

将包含x和y的动态集合合并为一个新的集合，假定在此操作前这两个集合是分离的。

所得集合的代表是Sx∪Sy的某个成员。

FIND(X)

返回包含x的集合的代表。

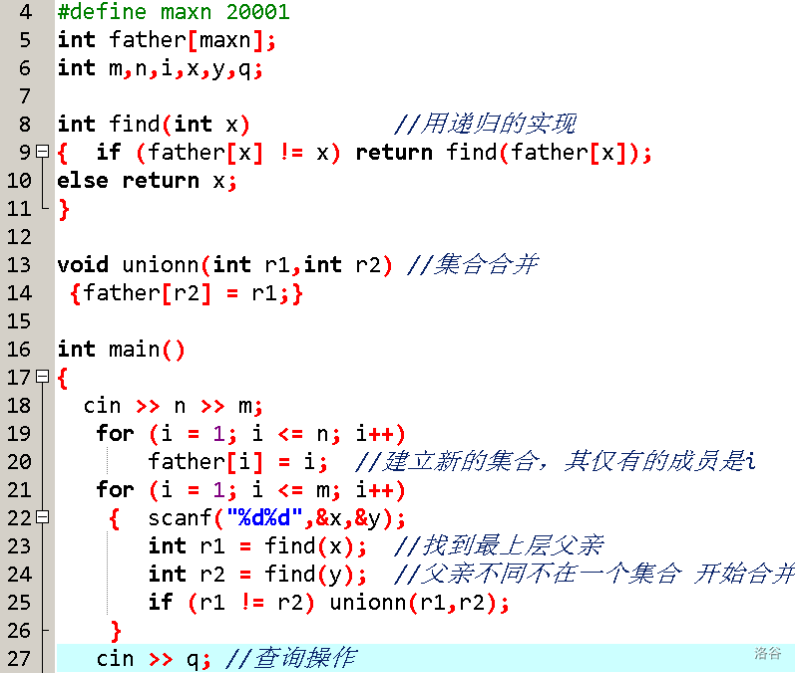
路径压缩

将元素的父亲指针全部指向根节点。

总结

初始化，

for(i=1;i<=n;i++)father[i]=i;

每个元素属于单独的一个集合,以自己作为根结点。

寻找根结点编号并压缩路径，

int find(int x){ 
	if(father[x]!=x) 
   father[x]=find(father[x]);
 　 return father[x];
   }

合并两个集合，

void unionn(int x,int y){
	x=find(x);
	y=find(y);
	father[y]=x; 
	}

判断元素是否属于同一集合，

bool judge(int x,int y){
	x=find(x);
   y=find(y);
   if(x==y)  
		return true;
	else 
		return false;
	}

并非原创，仅是整理，请见谅

Lo问我为什么看星星。我觉得银河和代码是同一种东西，这也是一种回答。————Co 【文章原创作者：韩国高防服务器 http://www.558idc.com/krgf.html 网络转载请说明出处】