英特尔数学核心函数库(Intel Math Kernel Library,MKL)是一套经过高度优化和广泛线程化的数学例程，专为需要极致性能的科学、工程及金融等领域的应用而设计。核心数学函数包括BLAS、LAPA
英特尔数学核心函数库(Intel Math Kernel Library,MKL)是一套经过高度优化和广泛线程化的数学例程，专为需要极致性能的科学、工程及金融等领域的应用而设计。核心数学函数包括BLAS、LAPACK、ScaLAPACK1、稀疏矩阵解算器、快速傅立叶转换、矢量数学及其它函数。其可以为英特尔处理器提供性能优化，并且更出色地与 Microsoft Visual Studio相集成。Intel MKL是一套经过高度优化和线程化的函数库，并提供了C和Fortran接口。
使用矩阵乘法(cblas_cgemm)为例来对比不同环境与配置的性能差距。
#include <stdio.h>
#include <stdlib.h>
#include "mkl.h" // 调用mkl头文件
#define min(x,y) (((x) < (y)) ? (x) : (y))
double* A, * B, * C; //声明三个矩阵变量，并分配内存
int m, n, k, i, j; //声明矩阵的维度，其中
double alpha, beta;
m = 2000, k = 200, n = 1000;
alpha = 1.0; beta = 0.0;
A = (double*)mkl_malloc(m * k * sizeof(double), 64); //按照矩阵维度分配内存
B = (double*)mkl_malloc(k * n * sizeof(double), 64); //mkl_malloc用法与malloc相似，64表示64位
C = (double*)mkl_malloc(m * n * sizeof(double), 64);
if (A == NULL || B == NULL || C == NULL) { //判空
mkl_free(A);
mkl_free(B);
mkl_free(C);
return 1;
}
for (i = 0; i < (m * k); i++) { //赋值
A[i] = (double)(i + 1);
}
for (i = 0; i < (k * n); i++) {
B[i] = (double)(-i - 1);
}
for (i = 0; i < (m * n); i++) {
C[i] = 0.0;
}
先定义出待乘矩阵\(A\)和\(B\)，拟执行\(C=A*B\)。其中\(C\)矩阵为全0，\(A\)和\(B\)矩阵设置为：
\[\begin{array}{l} A = \left[ {\begin{array}{*{20}{c}} {1.0}&{2.0}& \cdots &{1000.0}\\ {1001.0}&{1002.0}& \cdots &{2000.0}\\ \vdots & \vdots & \ddots & \cdots \\ {999001.0}&{999002.0}& \cdots &{1000000.0} \end{array}} \right] ~~~~~ B = \left[ {\begin{array}{*{20}{c}} {-1.0}&{-2.0}& \cdots &{-1000.0}\\ {-1001.0}&{-1002.0}& \cdots &{-2000.0}\\ \vdots & \vdots & \ddots & \cdots \\ {-999001.0}&{-999002.0}& \cdots &{-1000000.0} \end{array}} \right] \end{array} \]1 对比普通CPU与MKL库性能差距 1.1 使用dgemm(Sequential 串行)printf (" Making the first run of matrix product using Intel(R) MKL dgemm function \n"
" via CBLAS interface to get stable run time measurements \n\n");
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
printf (" Measuring performance of matrix product using Intel(R) MKL dgemm function \n"
" via CBLAS interface \n\n");
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
}
s_elapsed = (dsecnd() - s_initial) / LOOP_COUNT;
printf (" == Matrix multiplication using Intel(R) MKL dgemm completed == \n"
" == at %.5f milliseconds == \n\n", (s_elapsed * 1000));
输出为：
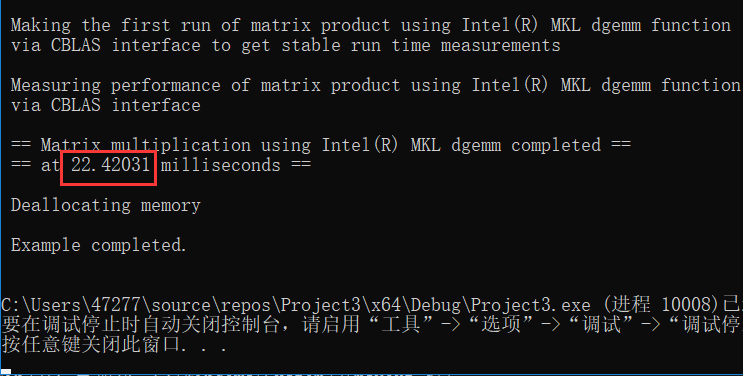1.2 使用嵌套循环(C)计算矩阵乘法
printf(" Measuring performance of matrix product using triple nested loop \n\n");
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
sum = 0.0;
for (k = 0; k < p; k++)
sum += A[p * i + k] * B[n * k + j];
C[n * i + j] = sum;
}
}
}
s_elapsed = (dsecnd() - s_initial) / LOOP_COUNT;
printf(" == Matrix multiplication using triple nested loop completed == \n"
" == at %.5f milliseconds == \n\n", (s_elapsed * 1000));
输出为：
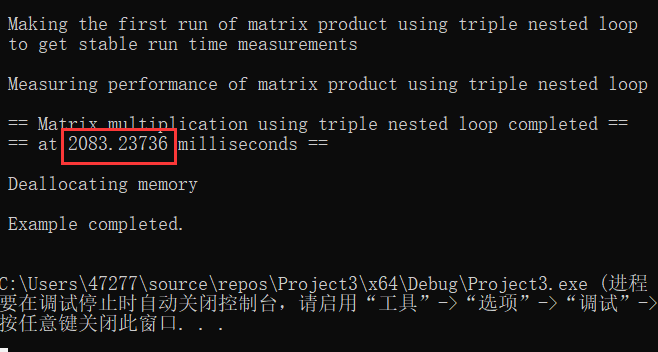2 对比串、并行与多线程差距
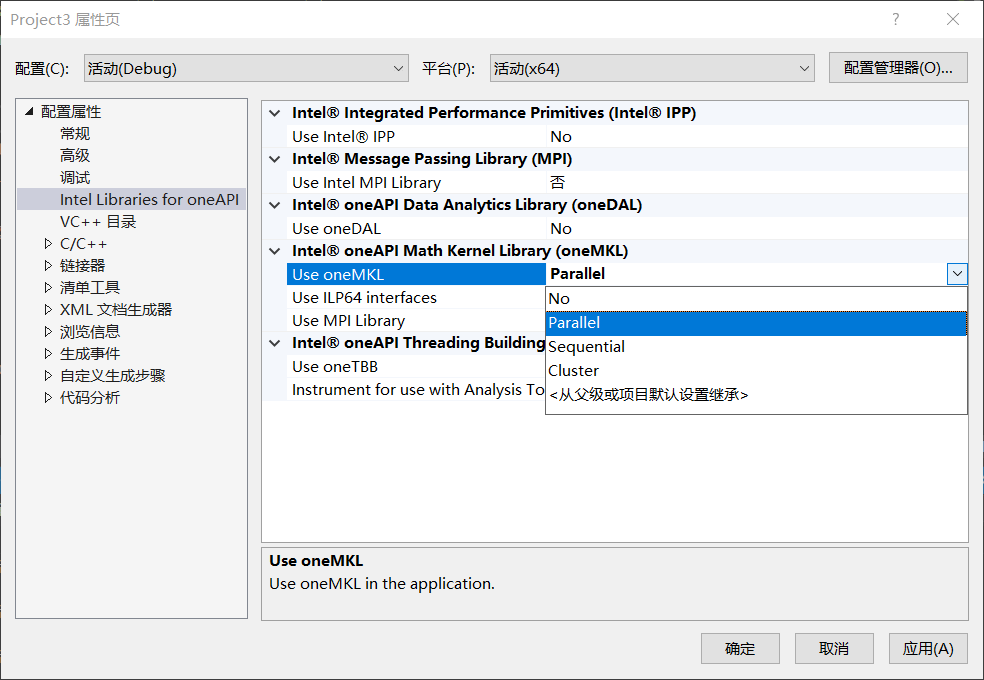
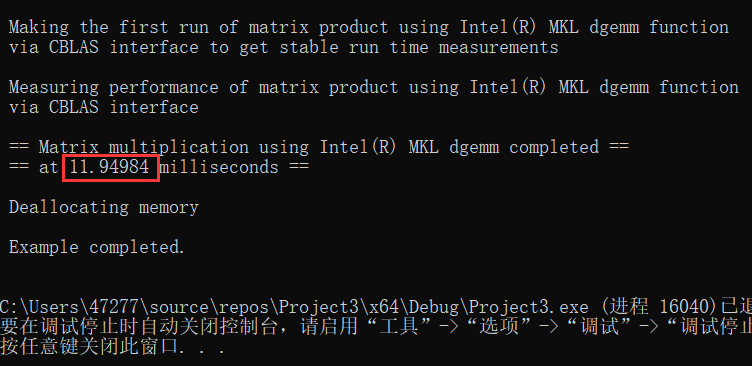
2.1 并行模式(Parallel)
2.2 多线程并行
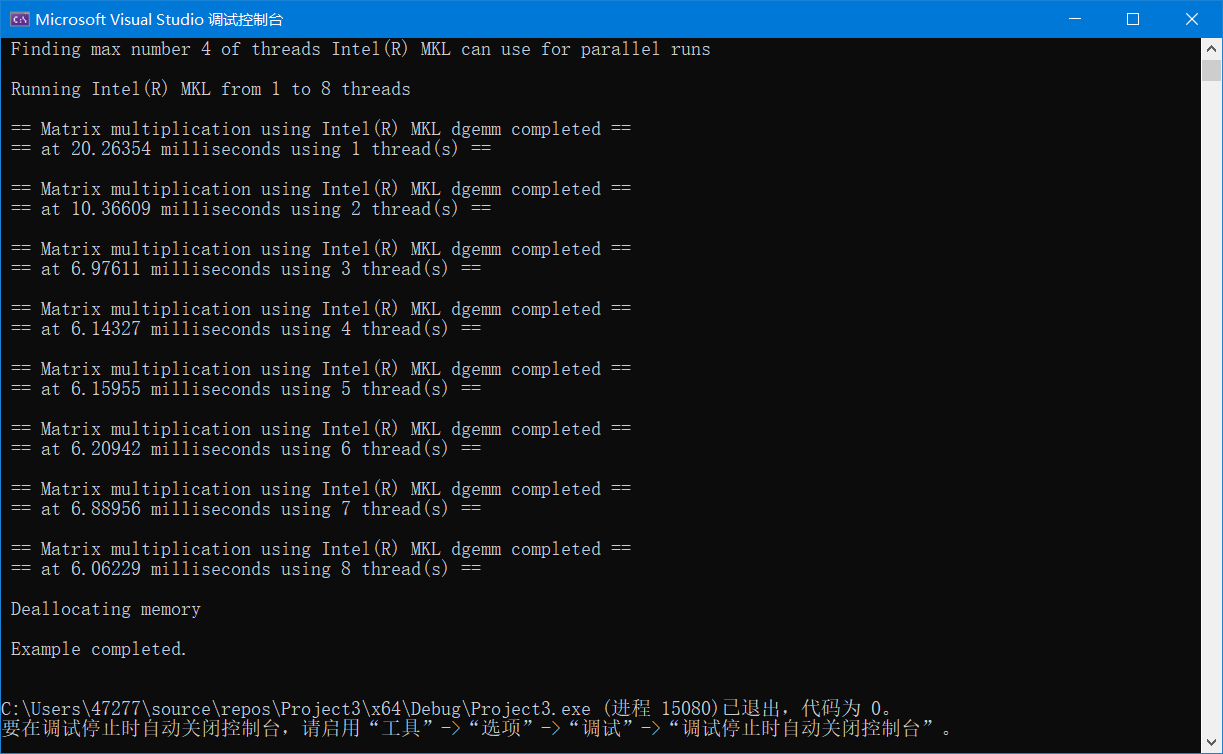
默认情况下，英特尔 MKL 使用 \(n\)个线程，其中 \(n\) 是系统上的物理内核数。 通过限制线程数量、观察 dgemm 的性能变化，以下示例展示了线程如何影响性能。
max_threads = mkl_get_max_threads();
printf (" Finding max number %d of threads Intel(R) MKL can use for parallel runs \n\n", max_threads);
printf (" Running Intel(R) MKL from 1 to %i threads \n\n", max_threads*2);
for (i = 1; i <= max_threads*2; i++) {
for (j = 0; j < (m*n); j++)
C[j] = 0.0;
mkl_set_num_threads(i);
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
}
s_elapsed = (dsecnd() - s_initial) / LOOP_COUNT;
printf (" == Matrix multiplication using Intel(R) MKL dgemm completed ==\n"
" == at %.5f milliseconds using %d thread(s) ==\n\n", (s_elapsed * 1000), i);
}
输出为：
完整代码
(I) dgemm_with_timing.c
#include <stdio.h>
#include <stdlib.h>
#include "mkl.h"
#define LOOP_COUNT 10
int main()
{
double *A, *B, *C;
int m, n, p, i, r;
double alpha, beta;
double s_initial, s_elapsed;
printf ("\n This example measures performance of Intel(R) MKL function dgemm \n"
" computing real matrix C=alpha*A*B+beta*C, where A, B, and C \n"
" are matrices and alpha and beta are double precision scalars\n\n");
m = 2000, p = 200, n = 1000;
printf (" Initializing data for matrix multiplication C=A*B for matrix \n"
" A(%ix%i) and matrix B(%ix%i)\n\n", m, p, p, n);
alpha = 1.0; beta = 0.0;
printf (" Allocating memory for matrices aligned on 64-byte boundary for better \n"
" performance \n\n");
A = (double *)mkl_malloc( m*p*sizeof( double ), 64 );
B = (double *)mkl_malloc( p*n*sizeof( double ), 64 );
C = (double *)mkl_malloc( m*n*sizeof( double ), 64 );
if (A == NULL || B == NULL || C == NULL) {
printf( "\n ERROR: Can't allocate memory for matrices. Aborting... \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
return 1;
}
printf (" Intializing matrix data \n\n");
for (i = 0; i < (m*p); i++) {
A[i] = (double)(i+1);
}
for (i = 0; i < (p*n); i++) {
B[i] = (double)(-i-1);
}
for (i = 0; i < (m*n); i++) {
C[i] = 0.0;
}
printf (" Making the first run of matrix product using Intel(R) MKL dgemm function \n"
" via CBLAS interface to get stable run time measurements \n\n");
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
printf (" Measuring performance of matrix product using Intel(R) MKL dgemm function \n"
" via CBLAS interface \n\n");
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
}
s_elapsed = (dsecnd() - s_initial) / LOOP_COUNT;
printf (" == Matrix multiplication using Intel(R) MKL dgemm completed == \n"
" == at %.5f milliseconds == \n\n", (s_elapsed * 1000));
printf (" Deallocating memory \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
printf (" Example completed. \n\n");
return 0;
}
#include <stdio.h>
#include <stdlib.h>
#include "mkl.h"
#define min(x,y) (((x) < (y)) ? (x) : (y))
#define LOOP_COUNT 10
int main()
{
double* A, * B, * C;
int m, n, p, i, j, k, r;
double alpha, beta;
double sum;
double s_initial, s_elapsed;
printf("\n This example measures performance of rcomputing the real matrix product \n"
" C=alpha*A*B+beta*C using a triple nested loop, where A, B, and C are \n"
" matrices and alpha and beta are double precision scalars \n\n");
m = 2000, p = 200, n = 1000;
printf(" Initializing data for matrix multiplication C=A*B for matrix \n"
" A(%ix%i) and matrix B(%ix%i)\n\n", m, p, p, n);
alpha = 1.0; beta = 0.0;
printf(" Allocating memory for matrices aligned on 64-byte boundary for better \n"
" performance \n\n");
A = (double*)mkl_malloc(m * p * sizeof(double), 64);
B = (double*)mkl_malloc(p * n * sizeof(double), 64);
C = (double*)mkl_malloc(m * n * sizeof(double), 64);
if (A == NULL || B == NULL || C == NULL) {
printf("\n ERROR: Can't allocate memory for matrices. Aborting... \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
return 1;
}
printf(" Intializing matrix data \n\n");
for (i = 0; i < (m * p); i++) {
A[i] = (double)(i + 1);
}
for (i = 0; i < (p * n); i++) {
B[i] = (double)(-i - 1);
}
for (i = 0; i < (m * n); i++) {
C[i] = 0.0;
}
printf(" Making the first run of matrix product using triple nested loop\n"
" to get stable run time measurements \n\n");
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
sum = 0.0;
for (k = 0; k < p; k++)
sum += A[p * i + k] * B[n * k + j];
C[n * i + j] = sum;
}
}
printf(" Measuring performance of matrix product using triple nested loop \n\n");
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
sum = 0.0;
for (k = 0; k < p; k++)
sum += A[p * i + k] * B[n * k + j];
C[n * i + j] = sum;
}
}
}
s_elapsed = (dsecnd() - s_initial) / LOOP_COUNT;
printf(" == Matrix multiplication using triple nested loop completed == \n"
" == at %.5f milliseconds == \n\n", (s_elapsed * 1000));
printf(" Deallocating memory \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
printf(" Example completed. \n\n");
return 0;
}
#include <stdio.h>
#include <stdlib.h>
#include "mkl.h"
#define LOOP_COUNT 10
int main()
{
double *A, *B, *C;
int m, n, p, i, j, r, max_threads;
double alpha, beta;
double s_initial, s_elapsed;
printf ("\n This example demonstrates threading impact on computing real matrix product \n"
" C=alpha*A*B+beta*C using Intel(R) MKL function dgemm, where A, B, and C are \n"
" matrices and alpha and beta are double precision scalars \n\n");
m = 2000, p = 200, n = 1000;
printf (" Initializing data for matrix multiplication C=A*B for matrix \n"
" A(%ix%i) and matrix B(%ix%i)\n\n", m, p, p, n);
alpha = 1.0; beta = 0.0;
printf (" Allocating memory for matrices aligned on 64-byte boundary for better \n"
" performance \n\n");
A = (double *)mkl_malloc( m*p*sizeof( double ), 64 );
B = (double *)mkl_malloc( p*n*sizeof( double ), 64 );
C = (double *)mkl_malloc( m*n*sizeof( double ), 64 );
if (A == NULL || B == NULL || C == NULL) {
printf( "\n ERROR: Can't allocate memory for matrices. Aborting... \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
return 1;
}
printf (" Intializing matrix data \n\n");
for (i = 0; i < (m*p); i++) {
A[i] = (double)(i+1);
}
for (i = 0; i < (p*n); i++) {
B[i] = (double)(-i-1);
}
for (i = 0; i < (m*n); i++) {
C[i] = 0.0;
}
max_threads = mkl_get_max_threads();
printf (" Finding max number %d of threads Intel(R) MKL can use for parallel runs \n\n", max_threads);
printf (" Running Intel(R) MKL from 1 to %i threads \n\n", max_threads*2);
for (i = 1; i <= max_threads*2; i++) {
for (j = 0; j < (m*n); j++)
C[j] = 0.0;
mkl_set_num_threads(i);
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
s_initial = dsecnd();
for (r = 0; r < LOOP_COUNT; r++) {
cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, p, alpha, A, p, B, n, beta, C, n);
}
s_elapsed = (dsecnd() - s_initial) / LOOP_COUNT;
printf (" == Matrix multiplication using Intel(R) MKL dgemm completed ==\n"
" == at %.5f milliseconds using %d thread(s) ==\n\n", (s_elapsed * 1000), i);
}
printf (" Deallocating memory \n\n");
mkl_free(A);
mkl_free(B);
mkl_free(C);
printf (" Example completed. \n\n");
return 0;
}