要想学好mysql,了解其支持的基本数据类型以及内部原理是极为重要的,只有这样,我们才能根据不同的业务要求来选择不同的数据类型,实现最佳的存储效果和查询性能,因而本文就着重总结一下mysql支持的数据类型以及内部的存储原理。
总体来说,mysql一共分成了四类:数值类型、日期和时间类型、字符串类型、二进制类型等。
数值类型数值类型是最为基础的类型,在业务开发中存储递增主键ID、金额、数量等属性时,都会经常选择数值类型来进行存储。整体上将数值类型分为整形、浮点型和定点数类型三类,其中整型对应我们现实生活中常用的整数类型;而浮点型则是对应现实生活中的小数类型;定点数类型则是为了存储精确的小数而被设计出来的。
整型整型之中,根据是否有符号又被分为无符号数和有符号数,同时不同存储空间以及整数表示范围的考量,整数类型又被分成了TINYINT、SMALLINT、MEDIUMINT、INT以及BIGINT五类,各个类别的类型以及所占空间和含义如下表所示:
非常小的整数 SMALLINT 2字节 0~\(2^{16}-1\) \(-2^{15}\)~\(2^{15}-1\) 小的整数 MEDIUMINT 3字节 0~\(2^{24}-1\) \(-2^{23}\)~\(2^{23}-1\) 中等大小的整数 INT(别名INTEGER) 4字节 0~\(2^{32}-1\) \(-2^{31}\)~\(2^{31}-1\) 标准的整数,跟Java中的int类型相同 BIGINT 8字节 0~\(2^{64}-1\) \(-2^{64}\)~\(2^{64}-1\) 大整数
具体使用时,为某个变量设定变量类型时加上对应的类型关键字即可;在区分无符号数以及有符号数时,则需要加上UNSIGINED关键字来加以区分,加上该关键字后,则表示使用的无符号数,比如TINYINT UNSIGNED表示的就是无符号TINYINT类型的数。
浮点型主要用来存储小数,其实现和存储范围和我们在其他编程语言中学习的类型,分为单精度浮点型(FLOAT)和双精度浮点型(DOUBLE)两类,两者的存储空间和表示范围如下表所示:
具体浮点数内部的存储原理以及存储范围的确定,感兴趣的同学可以参考之前写的一篇文章《"从内存角度分析浮点数大小比较方法"》此处不再赘述。
从表中可以看到浮点型数据可以将大量十进制小数转成二进制进行存储,但实际存储过程中许多小数存在误差,即存在精度损失。为了解决该问题,在MYSQL中引入了"定点数类型"来进行实现对小数的精确存储。
定点数类型定点类型作为精确存储小数的方式,它的设计思路和存储原理和浮点数有较大不同,其具体的结构如下表所示:
从表中可以看出一个定点数类型的数有两部分构成:
- M:表示该小数最多包含的有效数字个数。比如2.3有效数字个数为2;0.2,有效数字个数为1
- D:表示该小数保留小数点后十进制数字的个数,简单来讲就是小数的位数。比如2.3中D的值为1;8.321中D的值为3。
在存储时,为了保证定点数不损失小数精度,因而采用如下存储策略:
将十进制小数用小数点分隔开,分别把小数点左右的两个十进制整数存储起来
比如存储8.32时,分别将8和32分开存储,这样就相当于保存了8.32这一精确的小数。
具体使用时,不同的M和D值会影响到存储的小数范围,本着“能少用存储空间就少用存储空间”的原则,mysql在设计时,采用如下策略来对DECIMAL(M,D)数据类型分配存储空间,存储数据。我们以DECIMAL(16,4)为例:
- 第一步 划分位数:首先按照M和D的大小来划分,整数位和小数位,在本例中,总的有效数字位数为16,可存储的小数位数为4,可存储的整数位数为12。划分的示意图如下图所示:(注意在本图中,每一个方格代表的是十进制位而不是二进制位。)
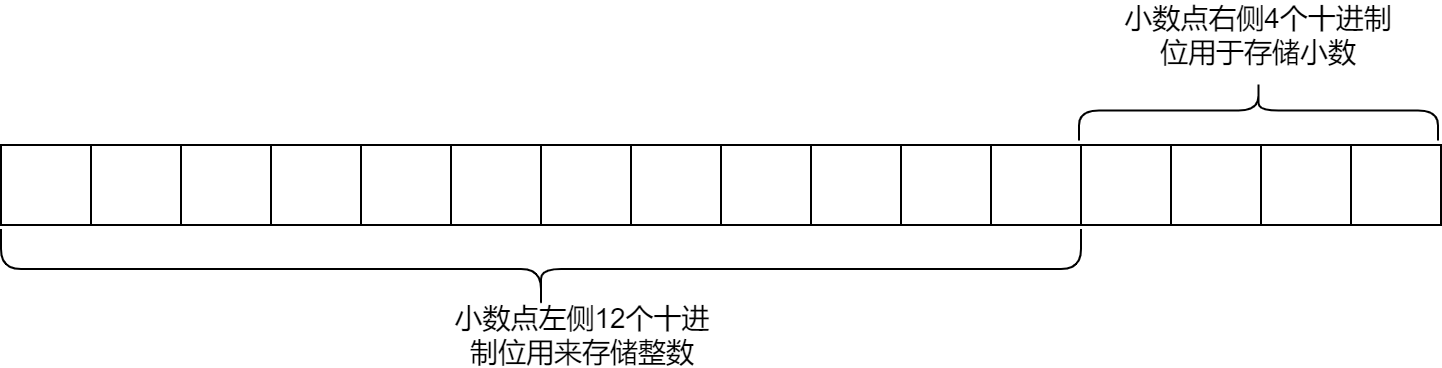
- 第二步 分组:从小数点位置开始,分别向两边进行分组操作,将每个整数每隔9个十进制位划分成一组,划分结果如下图所示:
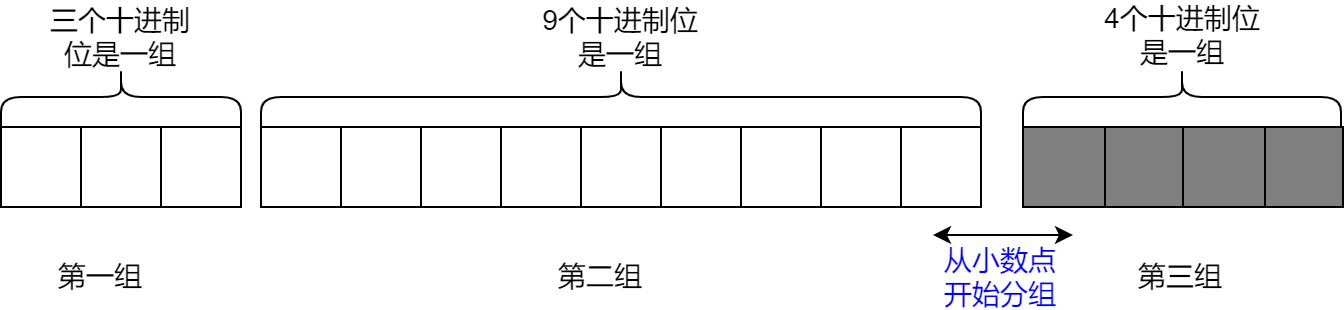
从图中可以看到,在分组时,如果不够9个十进制位,那么最终也会被单独划分成一组,比如第一组和第三组。
- 第三步 转换二进制:针对每个组中的十进制数字,分别将其转成二进制数字进行存储。为了有效利用存储空间,在存储时组中包含的十进制数字位数同步,则所占用的存储空间也不同,具体对应关系表如下:
从表中可以看出,在选择存储位数时,可表示的存储范围实际上是大于需要表示的数字范围的,因此此种存储方案是可行的的。当然有的小伙伴会问了,似乎这样存储是有空间浪费的?这也是没办法的事情,只能通过牺牲空间来缓存存储精度了,在工程实践中经常也会有这种tradeoff
