摘要本文记录阅读该paper的笔记。

本文给出两种MPSI协议,采用的是星型拓扑结构,即有一个leader,需要和其他参与者交互。优点是并非所有各方都必须同时在线:
(1)能抗半诚实攻击
- 通信复杂度与输入数据集大小呈线性关系;
- 计算复杂度是leader方输入数据的二次关系,其他参与者的输入集大小呈线性关系,后面可以使用两种hash可以消除此消耗。
(2)能抗恶意攻击
通信复杂度降为\(O((n^2+nm_{MAX}+nm_{MIN}logm_{MAX})k)\)bit,其中\(m_{MAX}\)和\(m_{MIN}\)分别为\(n\)个参与者的输入最大量和输入最小量
另外上面提到本文的半诚实方案是基于【FNP04】文章改进的,【FNP04】是最早提出MPSI的【Efficient private matching and set intersection-2013】,两方协议是:

画成图表示就是:
和下面介绍基于不经意多项式计算(OPE)的图是一样的。

MPC的安全性通常是通过两种对抗模型来证明的:
(1)半诚实模型
敌手遵循协议执行,但会试图从协议中获取更多信息。
(2)恶意模型
敌手在多项式时间内进行攻击

协议的优劣最根本的衡量方法就是计算消耗和通信消耗,MPSI主要分为两个方向:
(1)改进协议,计算任意布尔/算术电路
(2)协议能计算特定的函数,例如:计算\(k\)个相同元素,模式匹配和搜索问题,集合求交等

给出两种方法解决PSI问题:
(1)基于不经意多项式计算(OPE)

其中,需要用同态加密(乘法和加法),但是这是两方的PSI
(2)承诺不经意PRF计算
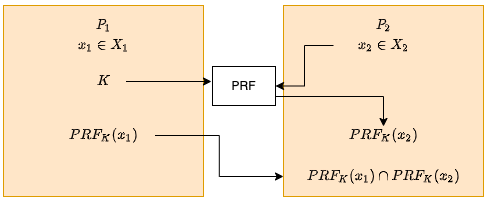
这里只使用PRF,来“隐藏”数据,安全性和性能有待确定。

(1)【Faster private set intersection based on OT extension】【Scalable private set intersection based on OT extension】给出了基于OT和布隆布过滤器的半诚实PSI协议
(2)【Improved private set intersection against malicious adversaries】给出基于OT和布隆布过滤器的抗恶意攻击PSI协议
(3)【Practical private set intersection protocols with linear com- plexity】【Linear-complexity private set intersection proto- cols secure in malicious model】【(if) size matters: Size-hiding private set intersection】使用了ROM(随机预言机)模型
(4)【When private set intersection meets big data: an efficient and scalable protocol】基于OT extension和混淆不隆过滤器设计的
MPC-PSI上面方案很少设计多方,都是两方间的PSI

上面的这三个方案,都是多方PSI,但通信复杂度高,对于大数据难以应用,效率低下。

其中【Multiparty computation from some- what homomorphic encryption】是在预处理阶段使用SWHE;【MASCOT: faster malicious arithmetic secure computation with oblivious transfer】在离线阶段计算,避免了不必要的在线计算量。

本文主要是设计了一个多方PSI协议,但是可以通过两方PSI实现多方PSI,能避免通信的二次开销。
采用具有加法同态性质的门限公钥密码方案,其中leader方输入的数据集可以很小,并将其数据进行hash,并提供两种hash方法:
(1)simple hashing
(2)balanced allocation hashing
使用这两个hash,通信量几乎相似,计算量(2)更优,且该动起来更复杂!


即给出\(p,g,g^x,g^y,g^{xr},g^{ys}\),难以区分\(g^d\)和\(g^{r+s}\)。

即给出\(p,g,g^x,g^y\),难以区分\(g^z\)和\(g^{xy}\)。



这里的history是什么意思?

可以看到这里的“加法同态”是:\(c_1*c_2=E(m_1+m_2)\)

(1)原始ElGamal方案

(2)门限ElGamal

需有多个私钥联合解密,增加了一个\(F_{DecZero}\)函数,是判断一个密文是否是0加密的。另外为了验证私钥的正确性,还需要ZKP.

方案的计算量主要是在\(P_1\)计算上,至少需要\(m_1*m_i\)比较,其中\(i\in [2,n]\)。为了减少计算量,使用hash函数,各方将自己的数据(item)映射/插入到\(B\)个不同的bin中。
只有映射在相同的bin才能比较,所以比较的次数减少为\(P_1\)的输入数量*一个bin中能装的最大item数量。(这里也能看出,一个bin是可以存放多个item)
simple hash
这里使用一个hash函数,即\(h\),将\(m\)个item插入到\(B\)个bin中,其中每个bin的容量最大为\(M\),即一个bin中最多能存放\(M\)个item。
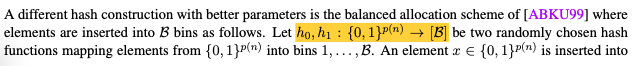

这里使用了两个hash函数\(h_0(),h_1()\),将\(m\)个item插入到\(B\)个bin中,其中每个bin的容量最大为\(M\)。
半诚实模型协议这里两个hash函数都使用了?还是选取一个使用?
(1)这是2PC协议:

- \(P_2\)获得私钥\(SK\)。
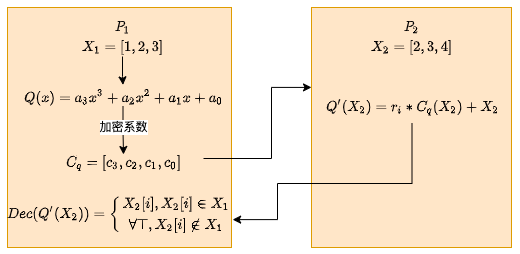
- \(P_2\)计算出多项式\(Q(.)\):即\(Q(x)=(x-x2_1)...(x-x2_{m_2})\),并将系数加密发送给\(P_1\)。
- \(P_1\)对于每一个元素\(x1_j\in X_1\),同态计算\(r_j*Q(x1_j)+x1_j\),并将结果发送给\(P_2\)。
注意:这里涉及到(密文明文、密文+密文、密文+明文),密文明文可以转换为明文+明文的加密。 - \(P_2\)收到后,解密每个结果,如果结果在\(X_2\)中,则说明是在交集中,否则不在。
另外,上面是\(P_2\)拥有私钥,\(P_2\)加密的系数,\(P_1\)只进行密文计算,\(P_2\)解密结果,并判断。
(2)首先对2PC协议改进:

这里说,\(P_2\)的功能不变,即产生多项式,加密系数;各方的密钥\((PK,SK_i)\);对于\(P_1\)中的元素\(x1_j\in X_1\),同态的计算\(r_j*Q(x1_j)\);\(P_1\)的功能就是聚合多项式计算和得出交集;这里把改造后的协议,各方的消息的发送表示为\(\pi_{FNP}^j,j\in (1,2)\)。
上面是改造后的两方协议,其中\(P_2\)生成多项式,加密系数,\(P_1\)同态的计算多项式,并联合\(P_2\)一起解密。下面完整协议中需要使用这个两方协议构造多方协议,即\(P_1\)还是同态的计算多项式,而其它方则扮演\(P_2\)的角色,生成多项式,加密系数,并最后和\(P_1\)一起解密!
(3)完整的多方PSI协议

完整的协议,分为三部分:
第一,各方运行\(\pi_{GEN}^{SH}\),协商出一个公钥,且不会泄露出各方的私钥。(意思就是各方都有一个私钥,这满足前面提到的门限加密)
第二,\(P_1\)使用改进后的2PC协议和各方交互得到系数密文。(也就是加密的Q(xi_j)\(系数)
第三,各方执行\)\pi _{DecZsro}^{SH}\(,\)P_1$得到所有的交集。
下面详细看:
输入:各方\(P_i\)的输入集合\(X_i=(x1_1,...,x1_{m_1})\),集合大小为\(m_1\),其中\(i\in [1,n]\)
第一:各方一起运行\(\pi_{GEN}^{SH}\),得到一个公钥\(PK\)和每人一个私钥\((SK_1,...,SK_n)\)
第二:\(P_1\)和各方(即\(P_2,...,P_n\))逐一执行协议\((\pi _{FNP}^{1},\pi _{FNP}^{2})\),得到结果密文\((ci_1,...,ci_{m_i})\),其中\(i\in [2,n]\)(这里如果是系数的话,不是应该有\(m_i+1\)个么?)
意思就是,各方\(P_i\)生成多项式\(Q(.)\),然后加密系数,将其发给\(P_1\),\(P_1\)再将所有的加密系数“整合”为一个加密的\(Q_1()\),并对于每一个元素同态的计算\(r_j*Q_1(x1_j)\)。
第三,就是计算交集。
从各方收到结果密文后,\(P_1\)计算:
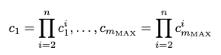
其中\(m_{MAX}=max(m_2,...,m_n)\),画个图理解一下:
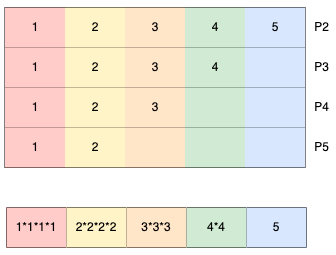
这里相当于\(P_1\)计算\(Q_1=Q_2()+...+Q_n()\)(别忘记了,这里使用的加法同态是:\(c_1*c_2=E(m_1+m_2)\))
这里的意思是,各方计算出\(Q_i()\),然后加密系数,发送给\(P_1\),\(P_1\)再将这些密文系数对应相加得到\(Q_1()\),再将\(P_1\)的集合元素代入,计算出\(m_1\)个结果,再将其解密,根据是否为0判断是交集!(和之前的协议相反,这里的加密是在各方进行,解密是在\(P_1\)执行,且需要联合各方(多个私钥))。
分析一下同态计算:
将多个加密的系数“整合”在一起,其实是想\(Q_2()+Q_3+...+Q_n()\),根据加法同态性,需要将密文系数相乘达到“相加”的效果。那么现在得到了\(Q_1()\)的密文系数,代入\(P_1\)的集合元素(明文),计算\(r_i*Q_1(x1_j)\),这里面涉及到密文明文(系数乘元素),密文+密文(计算后的各项相加),明文密文(随机数乘最终结果)。
通信和计算复杂度灵魂疑问:仅“加法”同态能实现么?

协议消耗主要是在门限加/解密(同态计算)和2PC协议。
(1)对于改进的2PC协议,通信消耗是在要传输\(m_2+1\)个密文;对于\(P_1\)的计算量又是巨大的,需要为每个元素都要执行\(O(m_2)\)的指数运算,对于全部的元素\(m_1\),则总共需要\(O(m_1.m_2)\)的指数元素。
(2)为了减少计算量,会使用hash函数,给出两种:simple hashing和balanced allocation hash

在该方案中,各方使用\(h\)hash函数,以\(P_2\)为例,每个bin中最多存储\(M\)个数,可以看成一个\(M\)次的多项式的根存储在一个bin中,如果不够\(M\)个,则可以填充0,结果就是有\(B\)个bin,即\(B\)个次数为\(M\)的多项式,\(m_2\)个非零根。
对于\(P_1\)来说,将每一个元素\(x1_j\)插入到一个bin中,然后计算对应的bin,就相当于计算多项式。
对于通信复杂度,需要发送\(B.M_i=O(m_i)\)个密文,其中\(M_i\)是用于分配\(P_1\)输入的bin大小在与\(P_i\)方交互时。
对于计算复杂度,\(P_1\)对于每一方需要\(O(M_i)\)的指数运算,总共需要执行\(O(m_1*\sum_{i}M_i)\)的指数元素。
使用balanced allocation hash这里存在一个疑问:\(M_i\)和\(m_i\)有什么区别?\(m_i\)是\(P_i\)方的集合大小,\(M_i\)是\(P_1\)与\(P_i\)交互时,\(P_1\)的输入对应的一个bin的容量。

这里使用两个hash函数,bin的个数\(B\)和最大容量\(M\)和simple hash不一样。
以\(P_2\)为例,将其\(m_2\)个元素插入到\(B\)个bin中的一个,其中每一个bin的最大容量为\(M\),这里是将每一个bin看作是一个\(M\)次的多项式。形成多项式\(Q_1(),...,Q_B()\),\(Q_i()\)的根在第\(i\)个bin中存储。
当\(P_1\)收到所有的加密多项式,同态计算出\(r0^j*Q_{h_1}(x1_j)\)和\(r1^j*Q_{h_1}(x1_j)\),将其相乘,解密后为0,则表明\(x1_j\)为交集元素。
恶意模型协议