Java 实现等频分箱

目录

• 等频离散法
• Python 实现方式
• Java 实现方式
• 测试结果对比
• 总结

等频离散法

---

根据数据的频率分布进行排序，然后按照频率进行离散，好处是数据变为均匀分布，但是会更改原有的数据结构。区间的边界值要经过选择，使得每个区间包含大致相等的实例数量。比如说 N=10 , 每个区间应该包含大约 10% 的实例。

Python 实现方式

---

等频法是将相同数量的记录放在每个区间，保证每个区间的数量基本一致。即将属性值分为具有相同宽度的区间，区间的个数 boxSize 根据实际情况来决定。比如有 60 个样本，我们要将其分为 boxSize=10 部分，则每部分的长度为 6 个样本。其缺点是边界易出现重复值，如果为了删除重复值可以设置 duplicates=‘drop’，但易出现于分片个数少于指定个数的问题

import pandas as pd  
import numpy as np  

data = np.random.randint(1,100,200)  
dd = pd.qcut(data, 10)  
print(str(dd.value_counts()))

运行结果：

Java 实现方式

---

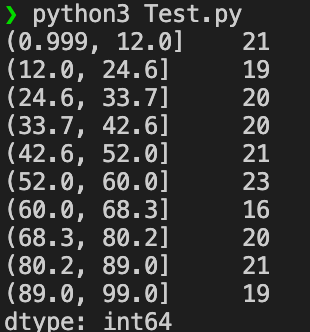
使用 Java 实现 Python 中的 qcut() 等频分箱后的 value_counts() 功能。

/**  
 * 等频分箱  
 *  
 * @param dataList 数据列表  
 * @param boxSize  分箱大小  
 */  
public static String quantileBasedDiscretion(List<BigDecimal> dataList, int boxSize) {  
    if (CollectionUtils.isEmpty(dataList) || 1 == dataList.size()) {  
        throw new RuntimeException("data set can not be null or size 1");  
    }   
	// 数据集排序  
    dataList = dataList.stream().sorted().map(value -> value.setScale(3, RoundingMode.HALF_UP))  
            .collect(Collectors.toList());  
  
    BigDecimal[] boxValue = new BigDecimal[boxSize + 1];  
    // 获取分位数对应的值  
    for (int i = 0; i <= boxSize; i++) {  
        double quantile = 1.0 * i / boxSize;  
        boxValue[i] = sortedListPercentile(dataList, quantile).setScale(3, RoundingMode.HALF_DOWN);  
    }    
	// 重新计算首部分箱值  
    boxValue[0] = boxValue[0].multiply(BigDecimal.valueOf(1 - 1e-10)).setScale(3, RoundingMode.FLOOR);  
    if (boxValue[0].compareTo(BigDecimal.ZERO) <= 0) {  
        boxValue[0] = boxValue[0].add(new BigDecimal("-0.001")).setScale(3, RoundingMode.FLOOR);  
    }    
	// 分箱操作  
    Map<String, Long> countMap = new LinkedHashMap<>();  
    for (int right = 1; right < boxValue.length; right++) {  
        int left = right - 1;  
        for (BigDecimal data : dataList) {  
            String key = "(" + boxValue[left] + ", " + boxValue[right] + "]";  
            if (data.compareTo(boxValue[left]) > 0 && data.compareTo(boxValue[right]) <= 0) {  
                countMap.compute(key, (k, value) -> value == null ? 1L : value + 1L);  
            }  
            countMap.putIfAbsent(key, 0L);  
        }  
    }  
    StringBuilder result = new StringBuilder();  
    countMap.forEach((key, value) -> result.append(key).append("\t").append(value).append("\n"));  
    // countMap.forEach((key, value) -> result.append(key).append(" ").append(value).append("|"));  
    return result.length() > 0 ? result.substring(0, result.length() - 1) : null;  
}  
  
/**  
 * 获取指定分位数的值  
 *  
 * @param numList 数据列表（排序后）  
 * @param p       分位点  
 */  
public static BigDecimal sortedListPercentile(List<BigDecimal> numList, double p) {  
    int n = numList.size();  
    BigDecimal px = BigDecimal.valueOf(p).multiply(BigDecimal.valueOf(n - 1));  
    BigDecimal i = px.setScale(0, RoundingMode.FLOOR);  
    BigDecimal g = px.subtract(i);  
    
    if (g.compareTo(BigDecimal.ZERO) == 0) {  
        return numList.get(i.intValue());  
    } else {  
        BigDecimal d1 = BigDecimal.ONE.subtract(g).multiply(numList.get(i.intValue())).setScale(2, RoundingMode.HALF_UP);  
        BigDecimal d2 = g.multiply(numList.get(i.intValue() + 1)).setScale(2, RoundingMode.HALF_UP);  
        return d1.add(d2);  
    }  
}

运行结果：

测试结果对比

---

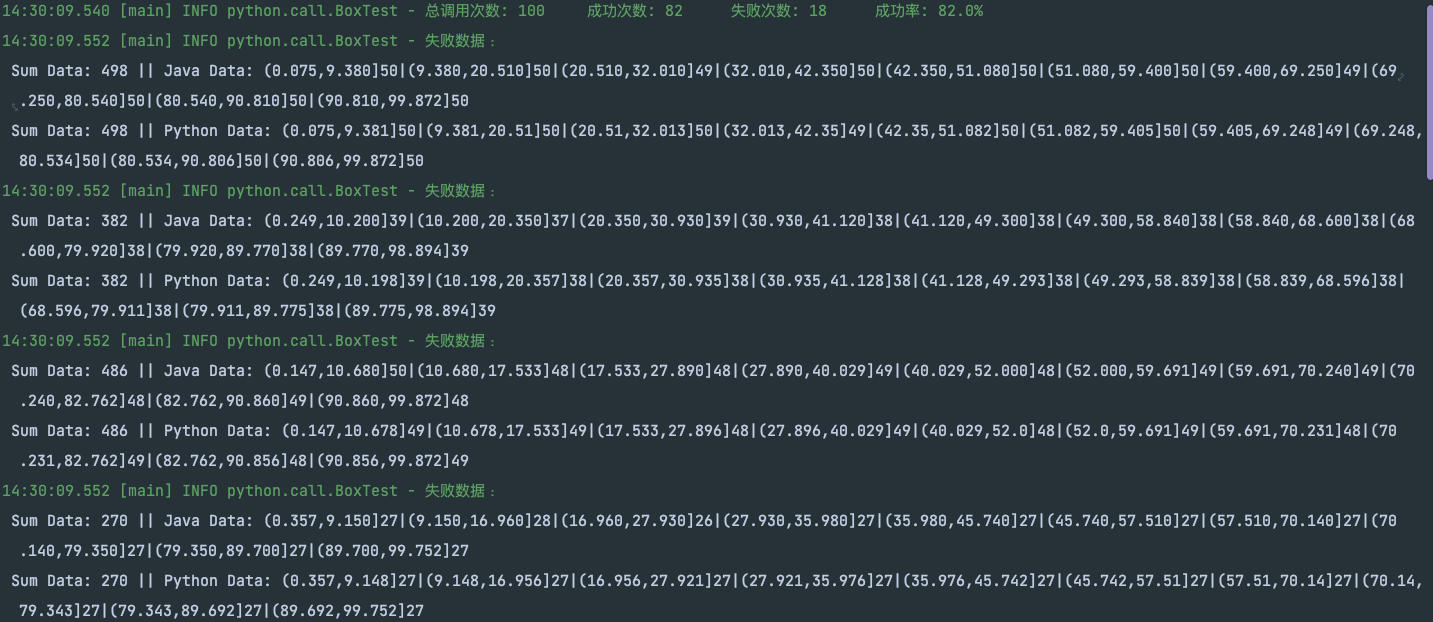
100 次运行结果差异对比

10000 次运行结果差异对比

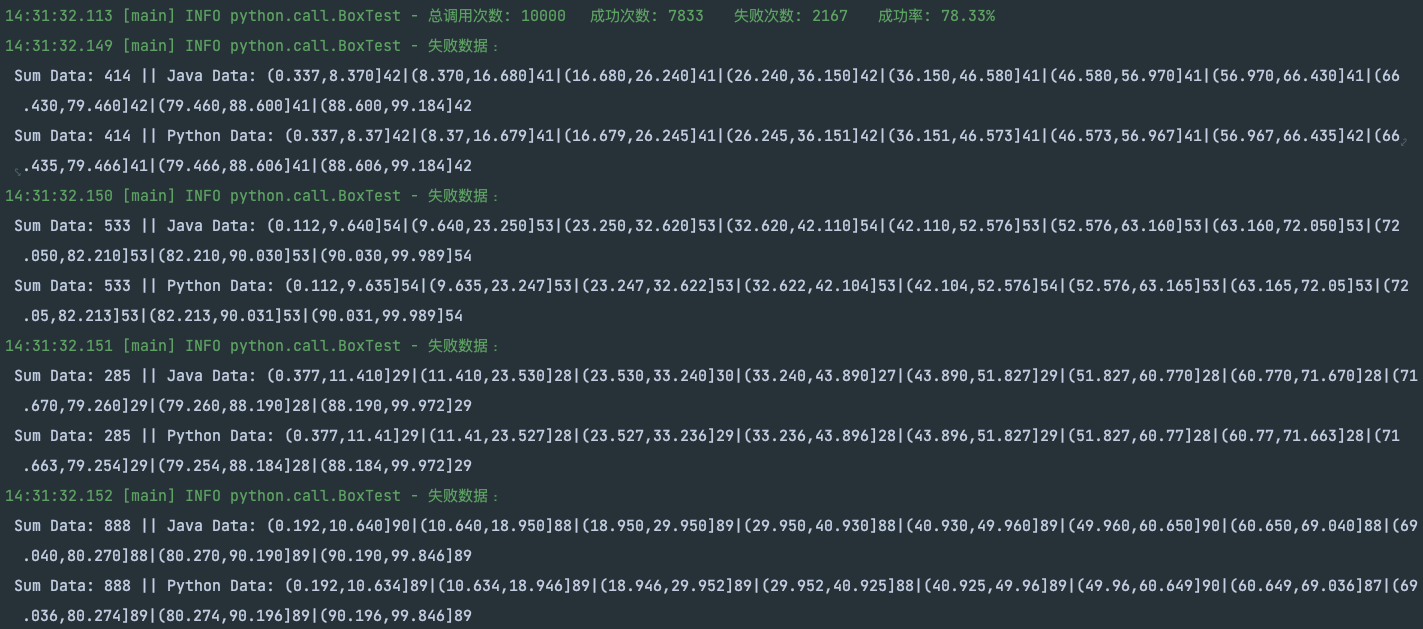
ps: 这里的分箱成功率使用的是每个区间分的的值作为判断依据。

由上图可以得出在 1 万条数据时，存在 22% 的数据与 Python 分箱后的值存在差异。但通过区间数据可以观测出统计范围误差在可容忍范围 (0.000 ~ 0.099) 内，且最终统计数据值之和均为相同的，不存在数据未分区的情况。

总结

---

这是一个简易的 Java 等频分箱功能实现。对比 Python 的 Pandas 库中 qcut() 方法还有很大的提升空间。包括如果边界出现重复值的问题处理等问题还未实现。功能实现仅供参考，希望能给大家带来帮助，也欢迎相互学习讨论~

参考文献：

Java 分位点 (分位值) 计算_0xYGC 的博客 - CSDN 博客_分位点怎么计算

python 数据分析之数据离散化 —— 等宽 & 等频 & 聚类离散_Mr 番茄蛋的博客 - CSDN 博客_python 数据离散化