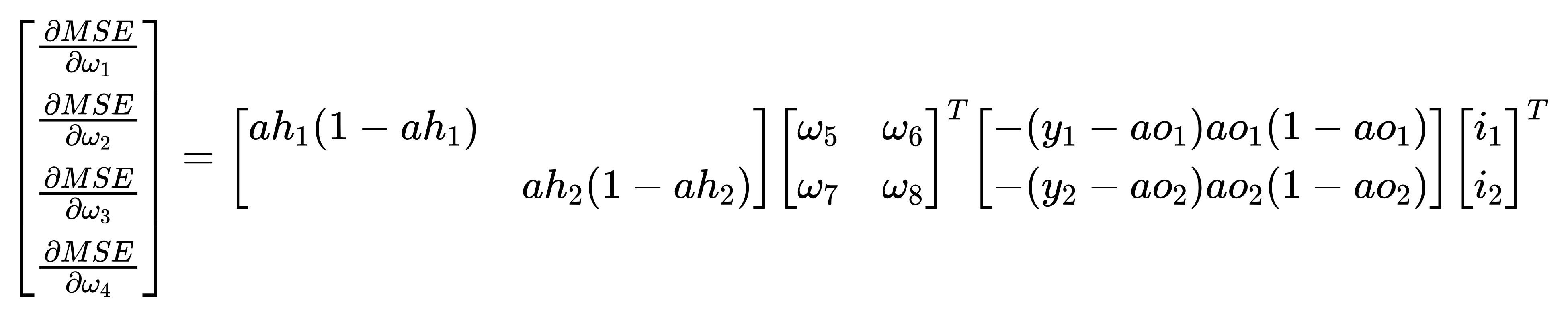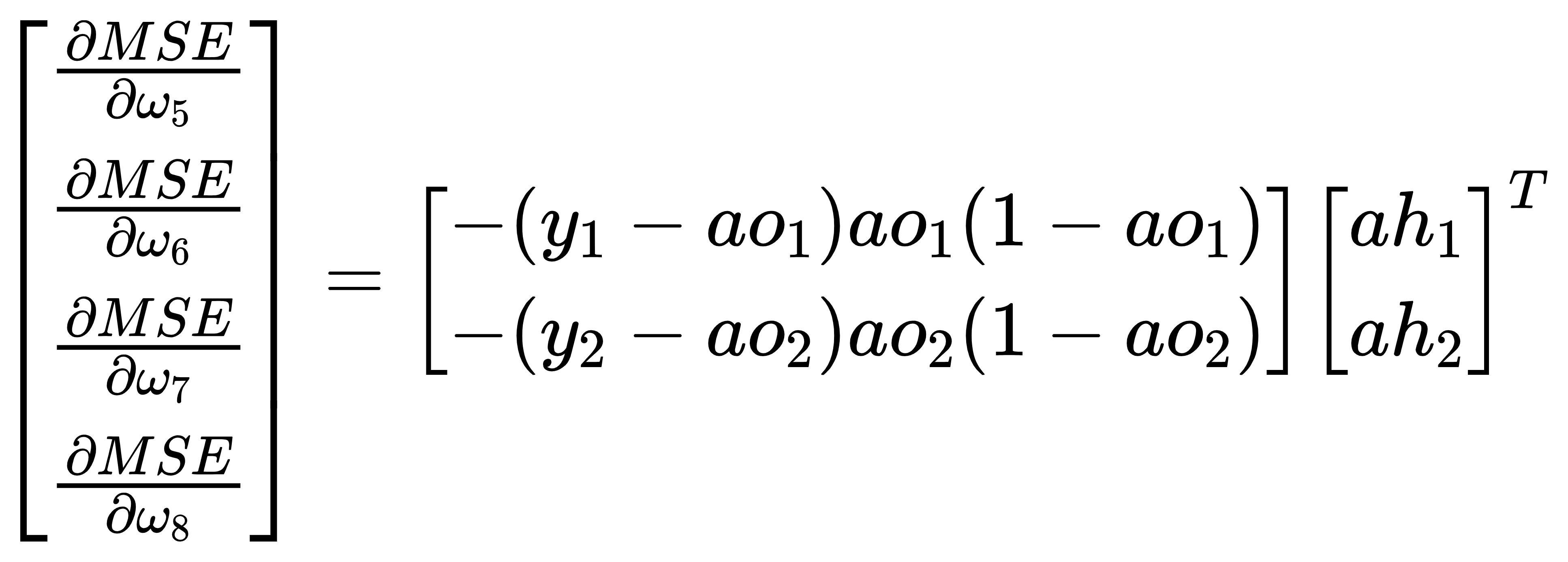经过上次从零开始训练神经网络---Keras【学习笔记】[1/2] 后,这次我们不借助Keras,自己使用代码编写并训练神经网络,以实现输入一张手写数字图片后,网络输出该图片对应的数字的目的。
基本要求我们的代码要导出三个接口,分别完成以下功能:
- 初始化initialisation,设置输入层,中间层,和输出层的节点数。
- 训练train:根据训练数据不断的更新权重值
- 查询query,把新的数据输入给神经网络,网络计算后输出答案。(推理)
一、建立一个类(class):下文将采用《Python Crash Course》2nd edition.,即蟒蛇书的代码扩充书写方式来展示我们逐步扩充神经网络代码的过程:
class NeuralNetWork:
"""一个全链接神经网络"""
def __init__(self):
"""
初始化网络,设置输入层,中间层,和输出层节点数
"""
pass
def train(self):
"""
根据输入的训练数据更新节点链路权重
"""
pass
def query(self):
"""
根据输入数据计算并输出答案
"""
pass
由于神经网络需要设定各层的节点数,以及学习率等“超参数”,来决定网络的结构、大小等性质。而这些超参数就可以在class的属性中初始化。
class NeuralNetWork:
"""一个全链接神经网络"""
def __init__(self, input_nodes, hidde_nnodes, output_nodes, learning_rate):
"""
初始化网络,设置输入层,中间层,和输出层节点数
:param input_nodes: 输入层节点数
:param hidden_nodes: 中间层(隐藏层)节点数
:param output_nodes: 输出层节点数
:param learning_rate: 学习率
"""
self.inodes = input_nodes
self.hnodes = hidden_nodes
self.onodes = output_nodes
self.lr = learning_rate
pass
--snip--
练习初始化一个输入层,中间层和输出层都有3个节点的3层神经网络。
input_nodes = 3
hidden_nodes = 3
output_nodes = 3
learning_rate = 0.3
n = NeuralNetWork(input_nodes, hidden_nodes, output_nodes, learning_rate)
2.2 初始化权重属性out:
由于前层输入进行层间传递到后层某个节点须服从wx+b形式,因此我们需要构造初始化的全中矩阵。
具体地,权重矩阵的形状应当遵守:
- 权重矩阵的列数 == 前层输入的个数(节点数)
- 权重矩阵的行数 == 后层接受的节点数
这一点不熟悉的,可以参考我之前的博客:练习推导一个最简单的BP神经网络训练过程【个人作业/数学推导】
由于权重不一定都是正的,它完全可以是负数,因此我们在初始化时,把所有权重初始化为-0.5到0.5之间。
class NeuralNetWork:
"""一个全链接神经网络"""
def __init__(self, input_nodes, hidde_nnodes, output_nodes, learning_rate):
"""
初始化网络,设置输入层,中间层,和输出层节点数
:param input_nodes: 输入层节点数
:param hidden_nodes: 中间层(隐藏层)节点数
:param output_nodes: 输出层节点数
:param learning_rate: 学习率
"""
self.inodes = input_nodes
self.hnodes = hidden_nodes
self.onodes = output_nodes
self.lr = learning_rate
"""
构造层间权重矩阵。
根据矩阵乘法。构造的权重矩阵的行数由后层节点数决定,列数由前层节点数决定。
"""
self.wih = numpy.random.rand(self.hnodes, self.inodes) - 0.5
# wih矩阵是一个(隐藏层节点数, 输入层节点数),各元素取值[-0.5, 0.5]的矩阵,符合要求。下同。
self.who = numpy.random.rand(self.onodes, self.hnodes) - 0.5
pass
--snip--
class NeuralNetWork:
"""一个全链接神经网络"""
--snip--
def query(self, inputs):
"""
根据输入数据计算并输出答案
:param inputs: 暂时理解为输入层的输入数据矩阵
"""
hidden_inputs = numpy.dot(self.wih, inputs)
# hidden_inputs是一个一维向量,每个元素对应着中间层某个节点从输入层神经元传过来后的信号量总和。
pass
前文提到前层输入进行层间传递到后层某个节点须服从wx+b形式。那么完成这一传递任务的就可以交给query()查询函数。
然而query()查询函数的任务不应该仅仅包括层间传递,还包括层内每个节点执行的激活函数运算,转化为该层的输出(或者是最终结果,或者是下一层的输入)。
sigmod激活函数在Python中可以直接调用,我们要做的就是准备好参数。我们可以先把这个函数在初始化函数中设定好。
class NeuralNetWork:
"""一个全链接神经网络"""
def __init__(self, input_nodes, hidde_nnodes, output_nodes, learning_rate):
"""
初始化网络,设置输入层,中间层,和输出层节点数
:param input_nodes: 输入层节点数
:param hidden_nodes: 中间层(隐藏层)节点数
:param output_nodes: 输出层节点数
:param learning_rate: 学习率
"""
self.inodes = input_nodes
self.hnodes = hidden_nodes
self.onodes = output_nodes
self.lr = learning_rate
"""
构造层间权重矩阵。
根据矩阵乘法。构造的权重矩阵的行数由后层节点数决定,列数由前层节点数决定。
"""
self.wih = numpy.random.rand(self.hnodes, self.inodes) - 0.5
# wih矩阵是一个(隐藏层节点数, 输入层节点数),各元素取值[-0.5, 0.5]的矩阵,符合要求。下同。
self.who = numpy.random.rand(self.onodes, self.hnodes) - 0.5
'''
scipy.special.expit对应的是sigmod函数.
使用Python保留关键字lambda构造匿名函数lambda x: scipy.special.expit(x)可以直接得到激活函数计算后的返回值。
'''
self.activation_function = lambda x: scipy.special.expit(x)
--snip--
def query(self, inputs):
"""
根据输入数据计算并输出答案
:param inputs: 输入层的输入数据矩阵
"""
hidden_inputs = numpy.dot(self.wih, inputs)
# hidden_inputs是一个一维向量,每个元素对应着中间层某个节点从输入层神经元传过来后的信号量总和。
pass
至此我们就可以分别调用激活函数计算中间层的输出信号,以及输出层经过激活函数后形成的输出信号。
class NeuralNetWork:
"""一个全链接神经网络"""
--snip--
def query(self, inputs):
"""
层间数据传递的计算,层内执行激活函数计算
:param inputs: 输入层的输入数据矩阵
:return: 神经网络一次正向传递的最终输出
"""
# 数据由输入层向中间层(隐藏层)进行层间传递,按照加权求和的规则计算
hidden_inputs = np.dot(self.wih, inputs)
# 数据在中间层(隐藏层)的接收端向输出端进行层内传递,经过激活函数后形成的输出数据矩阵
hidden_outputs = self.activation_function(hidden_inputs)
# 数据由中间层(隐藏层)向输出层进行层间传递,按照加权求和的规则计算
final_inputs = np.dot(self.who, hidden_outputs)
# 数据在输出层的接收端向输出端进行层内传递,经过激活函数后形成的最终的输出数据矩阵
final_outputs = self.activation_function(final_inputs)
print(final_outputs)
return final_outputs
到目前为止,我们不妨使用一组数据来测试一下神经网络框架的代码:
input_n = 3
hidden_n = 3
output_n = 3
learning_r = 0.3
n = NeuralNetWork(input_n, hidden_n, output_n, learning_r)
n.query([1.0, 0.5, -1.5])
四、训练train过程的实现out:
完成以上代码后,神经网络的大体框架就完成了,我们留下最重要的train函数,也就是通过训练样本训练链路权重的流程到下一步实现。
训练过程分两步:
- 计算输入训练数据,给出网络的计算结果,这点跟query()功能很像。(这正是我们完成query函数代码的原因)
- 将计算结果与正确结果相比对,获取误差,采用误差反向传播法更新网络里的每条链路权重。
我们先用代码完成第一步:
class NeuralNetWork:
"""一个全链接神经网络"""
--snip--
def train(self, inputs_list, targets_list):
"""
完成训练过程
:param inputs_list: 输入的训练数据
:param targets_list: 训练数据对应的正确结果
"""
inputs = np.array(inputs_list, ndmin=2).T
targets = np.array(targets_list, ndmin=2).T
# 数据由输入层向中间层(隐藏层)进行层间传递,按照加权求和的规则计算
hidden_inputs = np.dot(self.wih, inputs)
# 数据在中间层(隐藏层)的接收端向输出端进行层内传递,经过激活函数后形成的输出数据矩阵
hidden_outputs = self.activation_function(hidden_inputs)
# 数据由中间层(隐藏层)向输出层进行层间传递,按照加权求和的规则计算
final_inputs = np.dot(self.who, hidden_outputs)
# 数据在输出层的接收端向输出端进行层内传递,经过激活函数后形成最终的输出数据矩阵
final_outputs = self.activation_function(final_inputs)
pass
--snip--
可以发现与query()极其相似。
4.2 反向传播过程这里注意,如下反向传播计算式的形式是由我们使用的损失函数为MSE函数,以及上文提到激活函数为sigmoid函数共同决定的,某些资料里省略了。
class NeuralNetWork:
"""一个全链接神经网络"""
--snip--
def train(self, inputs_list, targets_list):
"""
完成训练过程
:param inputs_list: 输入的训练数据
:param targets_list: 训练数据对应的正确结果
"""
inputs = np.array(inputs_list, ndmin=2).T
targets = np.array(targets_list, ndmin=2).T
# 数据由输入层向中间层(隐藏层)进行层间传递,按照加权求和的规则计算
hidden_inputs = np.dot(self.wih, inputs)
# 数据在中间层(隐藏层)的接收端向输出端进行层内传递,经过激活函数后形成的输出数据矩阵
hidden_outputs = self.activation_function(hidden_inputs)
# 数据由中间层(隐藏层)向输出层进行层间传递,按照加权求和的规则计算
final_inputs = np.dot(self.who, hidden_outputs)
# 数据在输出层的接收端向输出端进行层内传递,经过激活函数后形成最终的输出数据矩阵
final_outputs = self.activation_function(final_inputs)
# (↓反向传播过程)
# 计算正向传播输出结果与标签的误差
output_errors = targets - final_outputs
hidden_errors = np.dot(self.who.T, output_errors * final_outputs * (1 - final_outputs))
# 按照链式求导法则求出损失函数MSE对各个权重w的偏导数,依据梯度下降法更新各权重
self.who += self.lr * np.dot((output_errors * final_outputs * (1 - final_outputs)), np.transpose(hidden_outputs))
self.wih += self.lr * np.dot((hidden_errors * hidden_outputs * (1 - hidden_outputs)), np.transpose(inputs)) # self.wih更新算式中,np.dot()的第一个参数表达式应用了“数组乘法”
pass
--snip--
想要看懂上述权重更新代码的提示:
- 要在数学上实现反向传播过程的推导,得到损失函数MSE对各权重wi的偏导数表达式;
- 根据”输入→中间层“和”中间层→输出层“,将偏导数分为两组∂MSE/∂[w1,w2,w3,w4]和∂MSE/∂[w5,w6,w7,w8];
- 将偏导数的多项式表达式形式,转换成矩阵乘法表达式形式;
- 转换时尽量做到矩阵形式中每一项的样子与数据在变量中存储形式一致,这样更容易理解和编写代码。
- 将某些步骤中“对角阵与列向量乘法”变成了更加容易用代码实现的“数组乘法”
- 权重更新语句是“+=”,是因为偏导数和梯度下降法均有“-”负负得正
五、导入数据训练神经网络如果上述代码和提示对你来说仍然过于“抽象”,那么请继续参考我之前写过的:练习推导一个最简单的BP神经网络训练过程【个人作业/数学推导】
其中对本文最重要结论如下图中展示的算式:
使用实际数据来训练我们的神经网络
5.1 “看”一下数据集(可选)class NeuralNetWork:
--snip--
data_file = open(".../mnist_test.csv") # 各位可以使用自己的数据集,这里.csv文件中存储的是10张(28,28)的手写数字图片,每张图片和其标签数据以一维数组(长度1+28*28)形式存在.csv的某行中。
data_list = data_file.readlines()
data_file.close()
print(len(data_list))
print(data_list[0])
# 把数据依靠','区分,并分别读入
all_values = data_list[0].split(',')
# 第一个值对应的是图片的标签,所以我们读取图片数据时要去掉第一个数值
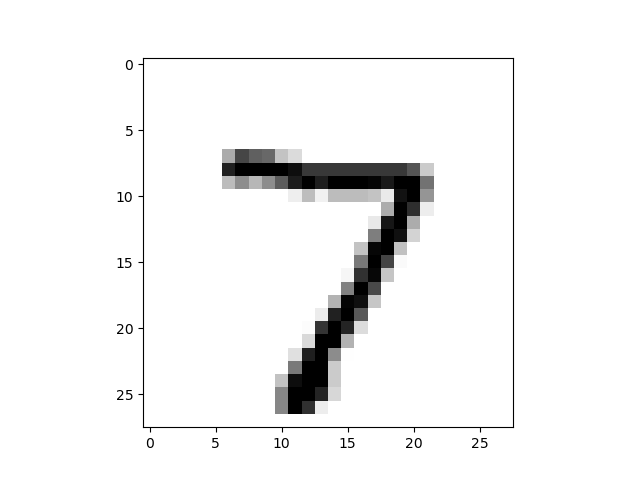
image_array = np.asfarray(all_values[1:]).reshape((28, 28))
plt.imshow(image_array, cmap='Greys', interpolation='None')
plt.show()
5.2 初始化神经网络Out:
有了神经网络,我们就能利用它将输入图片和对应的正确数字之间的联系,通过训练让神经网络“学会”它。
由于一张图片总共有28*28 = 784个数值,因此我们需要让网络的输入层具备784个输入节点。
这里需要注意的是,中间层的节点我们选择了100个神经元,这个选择是经验值。中间层的节点数没有专门的办法去规定,其数量会根据不同的问题而变化。
确定中间层神经元节点数最好的办法是实验,不停的选取各种数量,看看那种数量能使得网络的表现最好。
class NeuralNetWork:
--snip--
inputnodes = 784 # 28*28=784,是一个图片数据的像素个数
hiddennodes = 100 # 100:经验值
outputnodes = 10 # 一共10个数字,用10个节点即可输出one-hot编码对应格式的结果供判断
learningrate = 0.3
n = NeuralNetWork(inputnodes, hiddennodes, outputnodes, learningrate) # 实例化
--snip--
training_data_file = open(".../mnist_test.csv", 'r') # 只读模式加载数据,注意检查文件存储路径
training_data_list = training_data_file.readlines() # 将每一行数据作为一个元素,存储在一个list中
training_data_file.close() # 关闭文件
该步骤包含了训练截止条件设定(epoch),数据的归一化处理,数据标签的one-hot编码等过程。为保证代码不过于零碎,说明解释性文字采用代码注释的形式给出。
--snip--
epochs = 5 # 每个数据被遍历5次
for e in range(epochs):
for record in training_data_list:
all_values = record.split(',') # 把数据靠','分割,并分别读入
"""
接下来可以将数据“归一化”,也就是把所有数值全部转换到0.01到1.0之间。
由于表示图片的二维数组中,每个数大小不超过255,由此我们只要把所有数组除以255,就能让数据全部落入到0和1之间。
有些数值很小,除以255后会变为0,这样“有可能”导致链路权重更新出意想不到的问题。
所以我们需要把除以255后的结果先乘以0.99,然后再加上0.01,这样所有数据就处于0.01到1之间。
"""
inputs = (np.asfarray(all_values[1:])) / 255.0 * 0.99 + 0.01 # 首个元素是标签,在inputs读取时要去掉。进行“数据分割”。
# 设置图片与数值的对应关系,ont-hot编码
targets = np.zeros(outputnodes) + 0.01 # 创建一个10个元素的数组,各元素均为0.01
targets[int(all_values[0])] = 0.99 # 在数组中,将等同于数字值的索引的元素替换为0.99。假设数字7,就把索引7(第8个)数字更换为0.99
n.train(inputs, targets) # 启用训练过程
如果你觉得这个部分的功能应该在代码编写的时候作为class NeuralNetWork中train和query一样的一个方法,也可以自行改写或重写这段代码。
悄悄话:改写好的代码我已经放在文末的附录了~
--snip--
test_data_file = open(".../mnist_test.csv")
test_data_list = test_data_file.readlines()
test_data_file.close()
运用测试数据,通过query()函数让神经网络做出判断,正确得1分,错误得0分。
最后通过的分数占总次数的比值作为评估神经网络训练的指标。
--snip--
scores = [] # 设定一个列表记录每次判断的得分情况,判断正确存入1,错误存入0
for record in test_data_list:
all_values = record.split(',')
correct_number = int(all_values[0]) # 提取标签值
print("该图片对应的数字为:", correct_number)
inputs = (np.asfarray(all_values[1:])) / 255.0 * 0.99 + 0.01 # 归一化
outputs = n.query(inputs) # 让训练好的神经网络判断图片对应的数字并输出结果
label = np.argmax(outputs) # 应用numpy.argmax()函数找到数值最大的神经元对应的编号
print("网络认为图片的数字是:", label)
if label == correct_number:
scores.append(1)
else:
scores.append(0)
print(f"得分记录:\n{scores}")
# 计算图片判断的成功率
scores_array = np.asarray(scores)
print(f"perfermance = {scores_array.sum() / scores_array.size * 100}%")
运行一下,博主运行了四五次,正确率大概在80%~100%之间,如下分享部分运行日志:
某一次测试:
该图片对应的数字为: 7
神经网络判断输出结果:[0.04490563 0.1442118 0.01057779 0.03840048 0.10869915 0.10087318
0.02624607 0.50353098 0.01978388 0.3832254 ]
网络认为图片的数字是: 7
该图片对应的数字为: 2
神经网络判断输出结果:[0.03350826 0.19402964 0.8244046 0.03923834 0.10463468 0.11580433
0.0219085 0.01078036 0.03336618 0.20670527]
网络认为图片的数字是: 2
该图片对应的数字为: 1
神经网络判断输出结果:[0.05772382 0.82646153 0.08554279 0.026443 0.10922416 0.10826541
0.06526364 0.03217652 0.05343728 0.41798268]
网络认为图片的数字是: 1
该图片对应的数字为: 0
神经网络判断输出结果:[0.75354885 0.00469123 0.10610267 0.04624908 0.06654835 0.25189698
0.01219346 0.04163698 0.02263259 0.22938364]
网络认为图片的数字是: 0
该图片对应的数字为: 4
神经网络判断输出结果:[0.06560732 0.02923927 0.01173238 0.06191911 0.58371914 0.04675726
0.02078057 0.0478471 0.03739525 0.39723215]
网络认为图片的数字是: 4
该图片对应的数字为: 1
神经网络判断输出结果:[0.03902202 0.8389586 0.0657253 0.01908614 0.07016369 0.20796944
0.04493151 0.0493951 0.0317052 0.50017788]
网络认为图片的数字是: 1
该图片对应的数字为: 4
神经网络判断输出结果:[0.01736686 0.06961667 0.03573381 0.02303936 0.76090355 0.06674459
0.05125742 0.07640926 0.01028558 0.29533893]
网络认为图片的数字是: 4
该图片对应的数字为: 9
神经网络判断输出结果:[0.11019431 0.08369413 0.04207057 0.04246999 0.08058493 0.07806882
0.00777434 0.08662602 0.04694908 0.57857676]
网络认为图片的数字是: 9
该图片对应的数字为: 5
神经网络判断输出结果:[0.1498377 0.04490002 0.0911285 0.01397933 0.13341466 0.44113759
0.01476506 0.03469851 0.0448106 0.25640707]
网络认为图片的数字是: 5
该图片对应的数字为: 9
神经网络判断输出结果:[0.05914363 0.11508302 0.03964155 0.02739487 0.08430381 0.11847783
0.05053017 0.14199462 0.02186278 0.6277568 ]
网络认为图片的数字是: 9
得分记录:
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
perfermance = 100.0%
七,结语另一次测试
该图片对应的数字为: 7
神经网络判断输出结果:[0.02265905 0.03422366 0.06430731 0.03609857 0.22654582 0.09591944
0.02100579 0.75224205 0.01851069 0.12818351]
网络认为图片的数字是: 7
该图片对应的数字为: 2
神经网络判断输出结果:[0.10963591 0.09466725 0.80127158 0.04624556 0.06273288 0.0108084
0.02432404 0.01778638 0.02363708 0.12300765]
网络认为图片的数字是: 2
该图片对应的数字为: 1
神经网络判断输出结果:[0.09640155 0.77838901 0.02933256 0.04210427 0.11360658 0.06766493
0.052675 0.03493176 0.03070893 0.28625836]
网络认为图片的数字是: 1
该图片对应的数字为: 0
神经网络判断输出结果:[0.7237887 0.03547681 0.07877899 0.05324199 0.17120737 0.0149062
0.02448635 0.0682549 0.0351064 0.23182087]
网络认为图片的数字是: 0
该图片对应的数字为: 4
神经网络判断输出结果:[0.05946789 0.02326259 0.05029738 0.03110391 0.3446047 0.05265512
0.05653835 0.07649995 0.06696382 0.27745743]
网络认为图片的数字是: 4
该图片对应的数字为: 1
神经网络判断输出结果:[0.06971733 0.84624108 0.03975012 0.05342429 0.09792431 0.06858301
0.03652602 0.03837132 0.04676739 0.23421643]
网络认为图片的数字是: 1
该图片对应的数字为: 4
神经网络判断输出结果:[0.06727082 0.02175992 0.09172235 0.01222416 0.7647925 0.0728403
0.04735842 0.08916765 0.03130962 0.28624597]
网络认为图片的数字是: 4
该图片对应的数字为: 9
神经网络判断输出结果:[0.08551987 0.07957313 0.10618406 0.0102303 0.07864775 0.01744719
0.00578813 0.06349602 0.04352108 0.44316604]
网络认为图片的数字是: 9
该图片对应的数字为: 5
神经网络判断输出结果:[0.1020314 0.10072958 0.05474097 0.04504972 0.09402001 0.037387
0.0326212 0.07542155 0.02800163 0.05423302]
网络认为图片的数字是: 0
该图片对应的数字为: 9
神经网络判断输出结果:[0.08643607 0.1041881 0.02615816 0.01081672 0.1368236 0.04170109
0.00848632 0.07306719 0.03210684 0.85766101]
网络认为图片的数字是: 9
得分记录:
[1, 1, 1, 1, 1, 1, 1, 1, 0, 1]
perfermance = 90.0%
至此一个较为完整的神经网络的代码编写、训练和测试过程就完成了。不依托任何成熟的框架,使用常用的numpy等库完成了对手写数字的识别工作。
当然,我们要看到该神经网络并不是很“灵活”,例如:
- 激活函数和损失函数也是固定在代码和计算式之中的;
- 不能像Keras中那样增删层;
- 权重更新算法部分是根据“输入层→中间层(一层)→输出层”结构推导的结果,二者绑定性强;
- 没有根据损失函数的值来截止训练的功能
- 不能图形化输出神经网络结构,需要发挥个人想象力
- ......
将训练实例化的神经网络功能集成为class中的一个method的代码分享给大家。
注意集成后,后面实际训练的代码也要修改,这个就交给各位自行完成。
class NeuralNetWork:
--snip--
def network_train(self, data, epoches=5):
"""
完成整个训练网络的训练过程(权重更新过程)部分
:param data: 训练集,包含数据和标签
:param epoches: 数据被遍历次数
"""
for e in range(epoches):
for record_ in data:
all_values_ = record_.split(',') # 把数据依靠','分割,并分别读入
"""
接下来可以将数据“归一化”,也就是把所有数值全部转换到0.01到1.0之间。
由于表示图片的二维数组中,每个数大小不超过255,由此我们只要把所有数组除以255,就能让数据全部落入到0和1之间。
有些数值很小,除以255后会变为0,这样“有可能”导致链路权重更新出意想不到的问题。
所以我们需要把除以255后的结果先乘以0.99,然后再加上0.01,这样所有数据就处于0.01到1之间。
"""
inputs_ = (np.asfarray(all_values_[1:])) / 255.0 * 0.99 + 0.01 # 首个元素是标签,在inputs读取时要去掉。进行“数据分割”
# 设置图片与数值的对应关系,ont-hot编码
targets_ = np.zeros(self.onodes) + 0.01 # 创建一个10个元素的数组,各元素均为0.01
targets_[int(all_values_[0])] = 0.99 # 在数组中,将等同于数字值的索引的元素替换为0.99。假设数字7,就把索引7(第8个)数字更换为0.99
self.train(inputs_, targets_) # 启用训练过程
--snip--
#TODO 实际训练部分代码修改