Matplotlib 最开始被设计为仅支持二维的图表。到 1.0 版本发布左右,一些三维图表的工具在二维展示的基础上被创建了出来,结果就是 Matplotlib 提供了一个方便的(同时也是有限的)的可用于三维数据可视化的一套工具。三维图表可以使用载入mplot3d工具包来激活,这个包会随着 Matplotlib 自动安装:
from mpl_toolkits import mplot3d一旦模块被导入,三维 axes 就可以像其他普通 axes 一样通过关键字参数projection='3d'来创建:
import numpy as npimport matplotlib.pyplot as pltfig = plt.figure()
ax = plt.axes(projection='3d')plt.show()
三维 axes 激活后,我们可以在上面绘制不同的三维图表类型。三维图表在 notebook 中使用交互式图表展示会优于使用静态展示;回忆我们前面介绍过,你可以使用%matplotlib notebook而不是%matplotlib inline来激活交互式展示模式。
三维的点和线
三维图表中最基础的是使用(x, y, z)坐标定义的一根线或散点的集合。前面介绍过普通的二维图表,作为类比,使用ax.plot3D和ax.scatter3D函数可以创建三维折线和散点图。这两个函数的签名与二维的版本基本一致,你可以参考[简单折线图]和[简单散点图]来复习一下这部分的内容。下面我们绘制一个三维中的三角螺旋,在线的附近在绘制一些随机的点:
ax = plt.axes(projection='3d')# 三维螺旋线的数据
zline = np.linspace(0, 15, 1000)
xline = np.sin(zline)
yline = np.cos(zline)
ax.plot3D(xline, yline, zline, 'gray')
# 三维散点的数据
zdata = 15 * np.random.random(100)
xdata = np.sin(zdata) + 0.1 * np.random.randn(100)
ydata = np.cos(zdata) + 0.1 * np.random.randn(100)
ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='Greens');
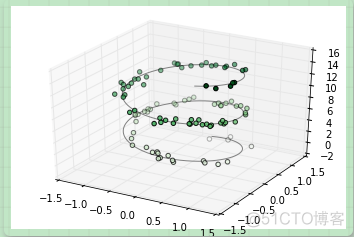
注意默认情况下,图中的散点会有透明度的区别,用于体现在图中散点的深度。虽然三维效果在静态图像中难以显示,你可以使用交互式的视图来获得更佳的三维直观效果。
三维轮廓图
类似于我们在[密度和轮廓图]中介绍的内容,mplot3d也包含着能够创建三维浮雕图像的工具。就像二维的ax.contour图表,ax.contour3D要求输入数据的格式是二维普通网格上计算得到的 Z 轴的数据值。下面我们展示一个三维的正弦函数轮廓图:
def f(x, y):return np.sin(np.sqrt(x ** 2 + y ** 2))
x = np.linspace(-6, 6, 30)
y = np.linspace(-6, 6, 30)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)fig = plt.figure()
ax = plt.axes(projection='3d')
ax.contour3D(X, Y, Z, 50, cmap='binary')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z');
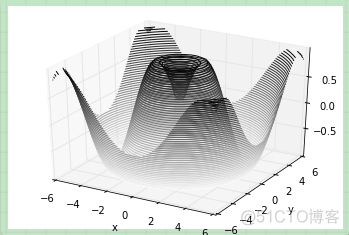
有时候默认的视角角度不是最理想的,在这种情况下我们可以使用view_init函数来设置水平角和方位角。在下面的例子中,我们使用的是 60° 的水平角(即以 60° 俯视 x-y 平面)和 35° 的方位角(即将 z 轴逆时针旋转 35°):
ax.view_init(60, 35)fig
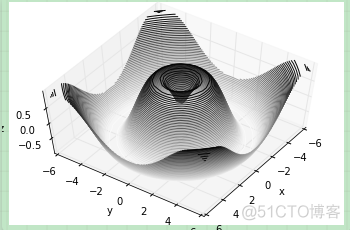
同样,注意到当使用 Matplotlib 交互式展示是,这样的旋转可以通过鼠标点击和拖拽来实现。
框线图和表面图
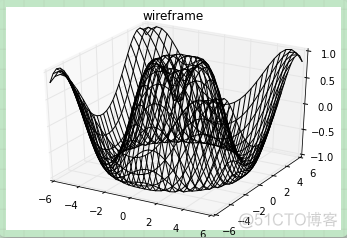
使用网格数据生成的三维图表还有框线图和表面图。这两种图表将网格数据投射到特定的三维表面,能够使得结果图像非常直观和具有说服力。下面是一个框线图的例子:
fig = plt.figure()ax = plt.axes(projection='3d')
ax.plot_wireframe(X, Y, Z, color='black')
ax.set_title('wireframe');
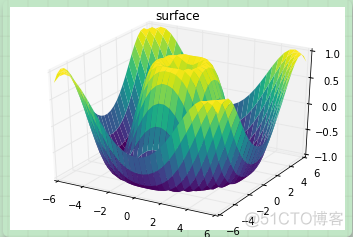
表面图类似框线图,区别在于每个框线构成的多边形都使用颜色进行了填充。添加色图用于填充多边形能够让图形表面展示出来:
ax = plt.axes(projection='3d')ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
cmap='viridis', edgecolor='none')
ax.set_title('surface');
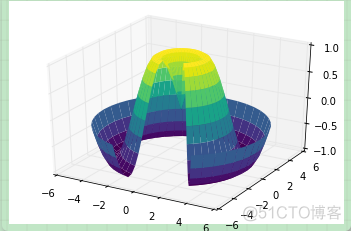
注意虽然每个颜色填充的表面都是二维的,但是表面的边缘不需要是直线构成的。下面的例子使用surface3D绘制了一个部分极坐标网格,能够让我们切入到函数内部观察效果:
r = np.linspace(0, 6, 20)theta = np.linspace(-0.9 * np.pi, 0.8 * np.pi, 40)
r, theta = np.meshgrid(r, theta)
X = r * np.sin(theta)
Y = r * np.cos(theta)
Z = f(X, Y)
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
cmap='viridis', edgecolor='none');
表面三角剖分
在一些应用场合中,上面的这种均匀网格绘制的图表方式太过于局限和不方便。在这些情况下,三角剖分的图表可以派上用场。如果我们并不是使用笛卡尔坐标系或极坐标系的网格来绘制三维图表,而是使用一组随机的点来绘制三维图表呢?
theta = 2 * np.pi * np.random.random(1000)r = 6 * np.random.random(1000)
x = np.ravel(r * np.sin(theta))
y = np.ravel(r * np.cos(theta))
z = f(x, y)ax = plt.axes(projection='3d')
ax.scatter(x, y, z, c=z, cmap='viridis', linewidth=0.5);
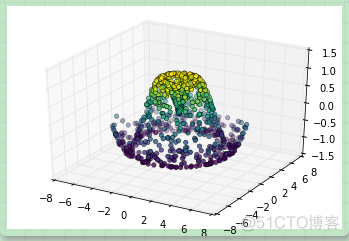
上图并未形象的表示出表面情况。这种情况下我们可以使用ax.plot_trisurf函数,它能首先根据我们的数据输入找到各点内在的三角函数形式,然后绘制表面(注意的是这里的 x,y,z 是一维的数组):
ax = plt.axes(projection='3d')ax.plot_trisurf(x, y, z,
cmap='viridis', edgecolor='none');
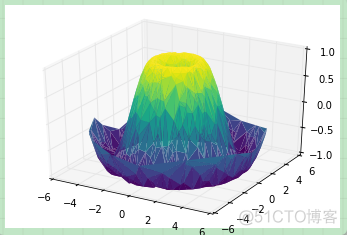
上图的结果很显然没有使用网格绘制表面图那么清晰,但是对于我们并不是使用函数构建数据样本(数据样本通常来自真实世界的采样)的情况下,这能提供很大的帮助。例如我们下面会看到,能使用这种方法绘制一条三维的莫比乌斯环。
例子:绘制莫比乌斯环

w = np.linspace(-0.25, 0.25, 8)
w, theta = np.meshgrid(w, theta)

现在我们已经有了所有需要获得三维坐标值的参数了。我们定义 为每个坐标点距离环形中间的位置,使用它来计算最终(x,y,z) 三维坐标系的坐标值:
# r是坐标点距离环形中心的距离值r = 1 + w * np.cos(phi)
# 利用简单的三角函数知识算得x,y,z坐标值
x = np.ravel(r * np.cos(theta))
y = np.ravel(r * np.sin(theta))
z = np.ravel(w * np.sin(phi))
最后,为了绘制对象,我们必须保证三角剖分是正确的。实现这个最好的方法是在底层的参数上面实现三角剖分,最后让 Matplotlib 将这个三角剖分投射到三维空间中形成莫比乌斯环。下面的代码最终绘制图形:
# 在底层参数的基础上进行三角剖分from matplotlib.tri import Triangulation
tri = Triangulation(np.ravel(w), np.ravel(theta))
ax = plt.axes(projection='3d')
ax.plot_trisurf(x, y, z, triangles=tri.triangles,
cmap='viridis', linewidths=0.2);
ax.set_xlim(-1, 1); ax.set_ylim(-1, 1); ax.set_zlim(-1, 1);
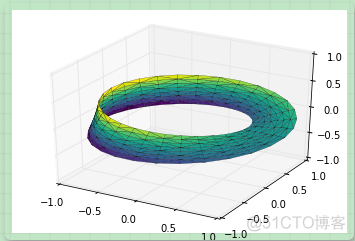
结合这些技巧,能够为你提供在 Matplotlib 创建和展现大量三维对象和模式的能力。
