Matplotlib基础--直方图，分桶和密度

接着上篇，一个简单的直方图可以是我们开始理解数据集的第一步。前面我们看到了 Matplotlib 的直方图函数，我们可以用一行代码绘制基础的直方图，当然首先需要将需要用的包导入 Pycharm：

import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-white')

data = np.random.randn(1000)plt.hist(data);plt.show()

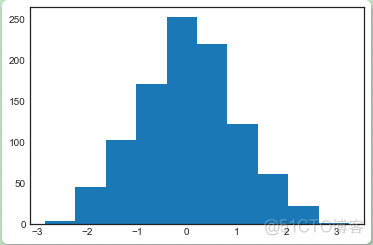
​​hist()​​函数有很多的参数可以用来调整运算和展示；下面又一个更加个性化的直方图展示：

译者注：normed 参数已经过时，此处对代码进行了相应修改，使用了替代的 density 参数。将上代码plt.hist(data);改为如下：

plt.hist(data, bins=30, density=True, alpha=0.5,
histtype='stepfilled', color='steelblue',
edgecolor='none');

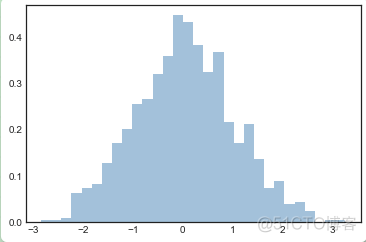
 ​​plt.hist​​​文档中有更多关于个性化参数的信息。作者发现联合使用​​histtype='stepfilled'​​​和​​alpha​​参数设置透明度在对不同分布的数据集进行比较展示时很有用：

x1 = np.random.normal(0, 0.8, 1000)
x2 = np.random.normal(-2, 1, 1000)
x3 = np.random.normal(3, 2, 1000)

kwargs = dict(histtype='stepfilled', alpha=0.3, density=True, bins=40)

plt.hist(x1, **kwargs)
plt.hist(x2, **kwargs)
plt.hist(x3, **kwargs);

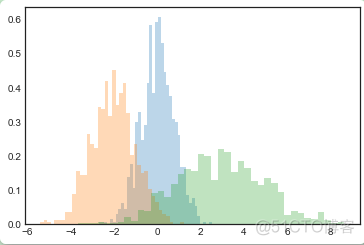
 如果你只是需要计算直方图的数值（即每个桶的数据点数量）而不是展示图像，​​np.histogram()​​函数可以完成这个目标：

counts, bin_edges = np.histogram(data, bins=5)
print(counts)

[ 49 273 471 183 24]

二维直方图和分桶

正如前面我们可以在一维上使用数值对应的直线划分桶一样，我们也可以在二维上使用数据对应的点来划分桶。本节我们介绍几种实现的方法。首先定义数据集，从多元高斯分布中获得​​x​​​和​​y​​数组：

mean = [0, 0]
cov = [[1, 1], [1, 2]]
x, y = np.random.multivariate_normal(mean, cov, 10000).T

​​plt.hist2d​​：二维直方图

绘制二维直方图最直接的方法是使用 Matplotlib 的​​plt.hist2d​​函数：

plt.hist2d(x, y, bins=30, cmap='Blues')
cb = plt.colorbar()
cb.set_label('counts in bin')

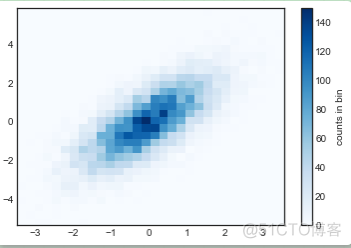
 类似​​plt.hist​​​，​​plt.hist2d​​​有许多额外的参数来调整分桶计算和图表展示，可以通过文档了解更多信息。而且，​​plt.hist​​​有​​np.histogram​​​，​​plt.hist2d​​​也有其对应的函数​​np.histogram2d​​。如下例：

counts, xedges, yedges = np.histogram2d(x, y, bins=30)

如果要获得更高维度的分桶结果，参见​​np.histogramdd​​函数文档。

​​plt.hexbin​​：六角形分桶

刚才的二维分桶是沿着坐标轴将每个桶分为正方形。另一个很自然的分桶形状就是正六边形。对于这个需求，Matplotlib 提供了​​plt.hexbin​​函数，它也是在二维平面上分桶展示，不过每个桶（即图表上的每个数据格）将会是六边形：

plt.hexbin(x, y, gridsize=30, cmap='Blues')
cb = plt.colorbar(label='count in bin')

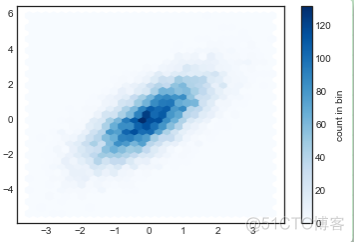
​​plt.hexbin​​有许多有趣的参数，包括能对每个点设置权重和将每个桶的输出数据结果改为任意的 NumPy 聚合结果（带权重的平均值，带权重的标准差等）。

核密度估计

另外一个常用来统计多维数据密度的工具是核密度估计（KDE）。这目前我们只需要知道 KDE 被认为是一种可以用来填补数据的空隙并补充上平滑变化数据的方法就足够了。快速和简单的 KDE 算法已经在​​scipy.stats​​模块中有了成熟的实现。下面我们就一个简单的例子来说明如何使用 KDE 和绘制相应的二维直方图：

from scipy.stats import gaussian_kde

mean = [0, 0]
cov = [[1, 1], [1, 2]]
x, y = np.random.multivariate_normal(mean, cov, 10000).T

# 产生和处理数据，初始化KDE
data = np.vstack([x, y])
kde = gaussian_kde(data)

# 在通用的网格中计算得到Z的值
xgrid = np.linspace(-3.5, 3.5, 40)
ygrid = np.linspace(-6, 6, 40)
Xgrid, Ygrid = np.meshgrid(xgrid, ygrid)
Z = kde.evaluate(np.vstack([Xgrid.ravel(), Ygrid.ravel()]))

# 将图表绘制成一张图像
plt.imshow(Z.reshape(Xgrid.shape),
origin='lower', aspect='auto',
extent=[-3.5, 3.5, -6, 6],
cmap='Blues')
cb = plt.colorbar()
cb.set_label("density")
plt.show()

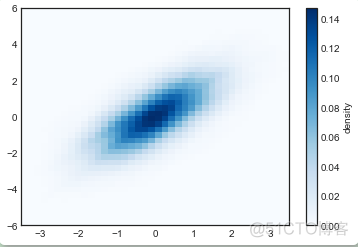
KDE 有着光滑的长度，可以在细节和光滑度中有效的进行调节（一个例子是方差偏差权衡）。这方面有大量的文献介绍：高斯核密度估计​​gaussian_kde​​使用了经验法则来寻找输入数据附近的优化光滑长度值。

其他的 KDE 实现也可以在 SciPy 中找到，每一种都有它的优点和缺点；

参见​​sklearn.neighbors.KernelDensity​​​和​​statsmodels.nonparametric.kernel_density.KDEMultivariate​​。要绘制基于 KDE 进行可视化的图表，Matplotlib 写出的代码会比较冗长。

【本文转自：日本cn2服务器 http://www.558idc.com/jap.html提供，感恩】