1 简介 编辑 编辑 2 完整代码 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%模拟球面 zernike clc clear all close all A=1000000000000000*ones([115 115]); zj=8; [M0 N0]=size(A); coef=zeros([1 zj]); RX = (M0+1)/2; RY = (N0+1)/2; R0 =m
1 简介

 编辑
编辑
 编辑
编辑
2 完整代码
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%模拟球面 zernikeclc
clear all
close all
A=1000000000000000*ones([115 115]);
zj=8;
[M0 N0]=size(A);
coef=zeros([1 zj]);
RX = (M0+1)/2;
RY = (N0+1)/2;
R0 =min(RX,RY);
fitted_ball=zeros([M0 N0]);
r=0;k=0;
z=0;
wfront=0;
for i = 1:M0
for j = 1:N0
rad = sqrt((i-RX)^2+(j-RY)^2);%椭圆的问题?
if rad <= R0;% &&A(i,j)~=0
r = rad/R0;
if r~=0
theta = atan2(RX-i,j-RY);
end
k=k+1;
wfront(k)=A(i,j);
z(1,k)=1;
z(2,k)=r*cos(theta);
z(3,k)=r*sin(theta);
z(4,k)=2*r^2-1;
z(5,k)=r^2*cos(2*theta);
z(6,k)=r^2*sin(2*theta);
z(7,k)=(3*r^3-2*r)*cos(theta);
z(8,k)=(3*r^3-2*r)*sin(theta);
end
end
end
orthop=zeros(zj,k);
orthop(1,1:k)=z(1,:);
bb(1)=wfront*orthop(1,:)'/(orthop(1,:)*orthop(1,:)');
zterm=zj;
for n=2:zterm
orthop(n,:)=z(n,:);
for m=1:n-1
aa(n,m)=z(n,:)*orthop(m,:)'/(orthop(m,:)*orthop(m,:)');
orthop(n,:)=orthop(n,:)-aa(n,m)*orthop(m,:);
end
bb(n)=wfront*orthop(n,:)'/(orthop(n,:)*orthop(n,:)');
end
coef(zterm)=bb(zterm);
for n=1:zterm-1
coef(zterm-n)=bb(zterm-n)-coef(zterm-n+1:zterm)*aa(zterm-n+1:zterm,zterm-n);
end
coef_ball=coef;
coef_ball(1:3)=0;coef_ball(5:zj)=0;
% coef_qiumian(1)=0;coef_qiumian(4)=0;
r=0;
zz=zeros([1 zterm]);
for i = 1:M0
for j = 1:N0
rad = sqrt((i-RX)^2+(j-RY)^2);
if rad <= R0
r = rad/R0;
if r~=0
theta = atan2(RX-i,j-RY);
end
zz(1)=1;
zz(2)=r*cos(theta);
zz(3)=r*sin(theta);
zz(4)=2*r^2-1;
zz(5)=r^2*cos(2*theta);
zz(6)=r^2*sin(2*theta);
zz(7)=(3*r^3-2*r)*cos(theta);
zz(8)=(3*r^3-2*r)*sin(theta);
fitted_ball(i,j)=coef_ball*zz';
end
end
end
figure(1),mesh(fitted_ball);
title('三维面形图','FontSize',10);
xlabel('x轴(pix)','FontSize',8);
ylabel('y轴(pix)','FontSize',8);
zlabel('面形','FontSize',8);
gst0=255*cos(fitted_ball*20);
gst1=imresize((gst0),[230 230],'bilinear');
figure(2),imshow(uint8(gst1));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 边界延拓
B=gst1(65:180,65:180);
figure(3),imshow(uint8(B));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% FFT相位提取%%%%%%%%%%%%
% %%%%%fft_lvbo%%%%%%%%%%%
C=imresize(B,[128 128]);
[m,n]=size(C);
% Af=fft2(double(C));
Af1=fft2(C);
Af2=fftshift(Af1);
figure(4),imshow(uint8(Af2));
%%%%%%%lvbo
filter0=ones([m n]);
filter0(1:(m/2),:)=0;
filter1=ones([m n]);
filter1((m/2+1):m,:)=0;%%%+1
filter2=ones([m n]);
filter2(:,1:(n/2))=0;
filter3=ones([m n]);
filter3(:,(n/2+1):n)=0;%%%+1
%Af2=abs(Af2);
Af3_0=filter0.*Af2;
Af3_1=filter1.*Af2;
Af3_2=filter2.*Af2;
Af3_3=filter3.*Af2;
%figure(5),imshow(uint8(Af3_0));
Af4_0=fftshift(Af3_0);
Af4_1=fftshift(Af3_1);
Af4_2=fftshift(Af3_2);
Af4_3=fftshift(Af3_3);
Aiff5_0=ifft2(Af4_0);
Aiff5_1=ifft2(Af4_1);
Aiff5_2=ifft2(Af4_2);
Aiff5_3=ifft2(Af4_3);
%%%%%%%%%%%%%%%%%%%%
J0=atan2(imag(Aiff5_0),real(Aiff5_0));
J1=atan2(imag(Aiff5_1),real(Aiff5_1));
J2=atan2(imag(Aiff5_2),real(Aiff5_2));
J3=atan2(imag(Aiff5_3),real(Aiff5_3));
%%%%%%%%%%%%%%%%%%%找中心
x=0;
r=ones([2 2]);
tp=2;
x0=0;
for x=3:(m-3)
% r=corrcoef(J0(x-1,:),J0(x,:))+corrcoef(J0(x,:),J0(x+1,:));
r=corrcoef(J0(x,:),J0(x+1,:));
if r(1,2)<tp
tp=r(1,2);
x0=x;
end
end
y=0;
r=ones([2 2]);
tp=2;
y0=0;
for y=3:(n-3)
% r=corrcoef(J2(:,y-1),J2(:,y))+corrcoef(J2(:,y),J2(:,y+1));
r=corrcoef(J2(:,y),J2(:,y+1));
if r(1,2)<tp
tp=r(1,2);
y0=y;
end
end
zx0=x0;
zy0=y0;
x0=x0+0.5;
y0=y0+0.5;
%%%%%%%%%%%
%J=filter0.*J0+filter1.*J1;
a1=(y0-1)/(x0-1);
b1=(x0-y0)/(x0-1);
a2=(n-y0)/(m-x0);
b2=(m*y0-n*x0)/(m-x0);
a3=(y0-1)/(x0-m);
b3=(m*y0-x0)/(m-x0);
a4=(y0-n)/(x0-1);
b4=(n*x0-y0)/(x0-1);
%%%%%%%%%%%
flt0=zeros([m n]);
flt1=zeros([m n]);
flt2=zeros([m n]);
flt3=zeros([m n]);
x=0;y=0;
% for x=(x0+1):m
% flt0(x,uint16(b3+a3*x):uint16(b2+a2*x))=1; %%(-1)*a*x ??
% end
% for x=1:x0
% flt1(x,uint16(b1+a1*x):uint16(b4+a4*x))=1;
% end
% for y=(y0+2):n
% %flt2((n+2-b*y):(b*y-1),y)=1;
% flt2(uint16((y-b4)/a4+2):uint16((y-b2)/a2-2),y)=1;
% end
% for y=1:(y0-1)
% % flt3((b*y+1):(n+1-b*y-1),y)=1;
% flt3(uint16((y-b1)/a1+1):uint16((y-b3)/a3-1),y)=1;
% end
for x=zx0:m
flt0(x,uint16(b3+a3*x):uint16(b2+a2*x))=1; %%(-1)*a*x ??
end
for x=1:zx0
flt1(x,uint16(b1+a1*x):uint16(b4+a4*x))=1;
end
for y=zy0:n
flt2(uint16((y-b4)/a4):uint16((y-b2)/a2),y)=1;
end
for y=1:zy0
flt3(uint16((y-b1)/a1):uint16((y-b3)/a3),y)=1;
end
%%%处理滤波器的重合点
f02=flt0+flt2;
f03=flt0+flt3;
f12=flt1+flt2;
f13=flt1+flt3;
f01=flt0+flt1;
for x=1:m
for y=1:n
if f02(x,y)==2
flt2(x,y)=0;
end
if f03(x,y)==2;
flt3(x,y)=0;
end
if f12(x,y)==2
flt2(x,y)=0;
end
if f13(x,y)==2;
flt3(x,y)=0;
end
if f01(x,y)==2;
flt1(x,y)=0;
end
end
end
J=flt0.*J0+flt1.*J1+flt2.*J2+flt3.*J3;
figure(6),mesh(double(J));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%j
%---基本方法解包裹---
[m n]=size(J);
k=double(zeros(m,n));
for j=1:n
for h=2:m
if (J(h,j)-J(h-1,j))>=pi
k(h,j)=k(h-1,j)-1;
elseif abs(J(h,j)-J(h-1,j))<pi
k(h,j)=k(h-1,j);
elseif (J(h,j)-J(h-1,j))<(-pi)
k(h,j)=k(h-1,j)+1;
end
end
end
for h=1:m
for p=2:n
if (J(h,p)-J(h,p-1))>=pi
k(h,p)=k(h,p-1)-1;
elseif abs(J(h,p)-J(h,p-1))<pi
k(h,p)=k(h,p-1);
elseif (J(h,p)-J(h,p-1))<(-pi)
k(h,p)=k(h,p-1)+1;
end
end
end
X=J+2*pi*k;
figure(7),mesh(double(X));
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 最小二乘解包裹%%%
% %%%%%%%边界处理
% F=spalloc(m*n,m*n,5*m*n);
% for w=1:m*n
% x=ceil(w/n)-1;y=rem(w,n);% w=i*n+j -->i j-->
% if y==0
% y=n;
% end
% if (x==0) && (y~=1&&y~=n)
% F(w,w)=-3;% F(w,(x-1)*n+y)=F(w,(i+1)*n+j)
% F(w,(x+1)*n+y)=1;
% % F(w,(x-1)*n+y)=1;
% F(w,x*n+y+1)=1;
% F(w,x*n+y-1)=1;
% end
% if (x==m-1) && (y~=1&&y~=n)
% F(w,w)=-3;% F(w,(x-1)*n+y)=F(w,(i+1)*n+j)
% % F(w,(x+1)*n+y)=1;
% F(w,(x-1)*n+y)=1;
% F(w,x*n+y+1)=1;
% F(w,x*n+y-1)=1;
% end
% if (y==1) && (x~=0&&x~=m-1)
% F(w,w)=-3;% F(w,(x-1)*n+y)=F(w,(i+1)*n+j)
% F(w,(x+1)*n+y)=1;
% F(w,(x-1)*n+y)=1;
% F(w,x*n+y+1)=1;
% % F(w,x*n+y-1)=1;
% end
% if (y==n) && (x~=0&&x~=m-1)
% F(w,w)=-3;% F(w,(x-1)*n+y)=F(w,(i+1)*n+j)
% F(w,(x+1)*n+y)=1;
% F(w,(x-1)*n+y)=1;
% % F(w,x*n+y+1)=1;
% F(w,x*n+y-1)=1;
% end
% if (x==0) && (y==1) % &&y~=n)
% F(w,w)=-2;% F(w,(x-1)*n+y)=F(w,(i+1)*n+j)
% F(w,(x+1)*n+y)=1;
% % F(w,(x-1)*n+y)=1;
% F(w,x*n+y+1)=1;
% % F(w,x*n+y-1)=1;;
% end
% if (x==m-1) && (y==1)% &&y~=n)
% F(w,w)=-2;% F(w,(x-1)*n+y)=F(w,(i+1)*n+j)
% % F(w,(x+1)*n+y)=1;
% F(w,(x-1)*n+y)=1;
% F(w,x*n+y+1)=1;
% % F(w,x*n+y-1)=1;;
% end
% if (x==m-1) && (y==n)% &&y~=n)
% F(w,w)=-2;% F(w,(x-1)*n+y)=F(w,(i+1)*n+j)
% % F(w,(x+1)*n+y)=1;
% F(w,(x-1)*n+y)=1;
% % F(w,x*n+y+1)=1;
% F(w,x*n+y-1)=1;;
% end
% if (x==0) && (y==n)% &&y~=n)
% F(w,w)=-2;% F(w,(x-1)*n+y)=F(w,(i+1)*n+j)
% F(w,(x+1)*n+y)=1;
% % F(w,(x-1)*n+y)=1;
% % F(w,x*n+y+1)=1;
% F(w,x*n+y-1)=1;;
% end
% if (x>0&&x<m-1)&&(y>1&&y<n)
% F(w,w)=-4;
% F(w,(x+1)*n+y)=1;
% F(w,(x-1)*n+y)=1;
% F(w,x*n+y+1)=1;
% F(w,x*n+y-1)=1;
% end
% end
%
% %%--建立泊松方程
% dx=zeros(m,n);
% dy=zeros(m,n);
% bx=(zeros(m,n));
% by=(zeros(m,n));
% for lx=1:(m-1)
% for ly=1:n
% %dx(lx,ly)=J(lx+1,ly)-J(lx,ly);%dx(lx,:)=..
% if J(lx+1,ly)-J(lx,ly)>=pi
% bx(lx,ly)=0-1;
% elseif J(lx+1,ly)-J(lx,ly)<-pi
% bx(lx,ly)=0+1;
% else
% bx(lx,ly)=0;
% end
% dx(lx,ly)=J(lx+1,ly)-J(lx,ly)+2*pi*bx(lx,ly);%%NOTE: bb的形式!!!need to change
% end
% end
% for lx=1:m
% for ly=1:(n-1)
% % dy(lx,ly)=J(lx,ly+1)-J(lx,ly);% !tongshang
% if (J(lx,ly+1)-J(lx,ly))>=pi
% by(lx,ly)=0-1;
% elseif (J(lx,ly+1)-J(lx,ly))<-pi
% by(lx,ly)=0+1;
% else
% by(lx,ly)=0;
% end
% dy(lx,ly)=J(lx,ly+1)-J(lx,ly)+2*pi*by(lx,ly);%%NOTE: bb的形式!!!need to change
% end
% end
% dx(m,:)=0;
% dy(:,n)=0;
% R=zeros(m,n);
% % R(1,2:n)=dx(1,2:n)-0+dy(1,2:n)-dy(1,1:(n-1));
% % R(2:m,1)=dx(2:m,1)-dx(1:(m-1),1)+dy(2:m,1)-0;
% % R(1,1)=dx(lx,ly)+dy(lx,ly);
% for lx=1:m
% for ly=1:n
% if (lx==1)&&(ly~=1)
% R(lx,ly)=dx(lx,ly)+dy(lx,ly)-dy(lx,ly-1);
% elseif (ly==1)&&(lx~=1)
% R(lx,ly)=dx(lx,ly)-dx(lx-1,ly)+dy(lx,ly);
% elseif (ly==1)&&(lx==1)
% R(lx,ly)=dx(lx,ly)+dy(lx,ly);
% else
% R(lx,ly)=dx(lx,ly)-dx(lx-1,ly)+dy(lx,ly)-dy(lx,ly-1);
% end
% end
% end
% %%%%%%%%%%%%%解方程%%%%!!!!!!!!!!RR=wiener2(R,[10 10]);
% for g=1:m
% for t=1:n
% GG((g-1)*n+t)=R(g,t);
% end
% end
% GT=GG';
%
% TT=cgs(F,GT,1e-006,100);%300
% X=zeros(m,n);
% for g=1:m
% for t=1:n
% X(g,t)=TT((g-1)*n+t);%/2%%%%%2倍关系
% end
% end
% figure(8),mesh(double(X));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Zernike拟合%%%%%%
A=imresize(X,[65 65],'bilinear');
zj=16;
[M0 N0]=size(A);
coef(1:zj) = 0;
RX = (M0+1)/2;
RY = (N0+1)/2;
R0 =min(RX,RY);
% fitted(1:M0,1:N0) = 0;
fitted_qulijiao=zeros([M0 N0]);
% fitted_ball=zeros([M0 N0]);
r=0;k=0;
z=0;
wfront=0;
for i = 1:M0
for j = 1:N0
rad = sqrt((i-RX)^2+(j-RY)^2);%椭圆的问题?
if rad <= R0;% &&A(i,j)~=0
r = rad/R0;
if r~=0
theta = atan2(RX-i,j-RY);
end
k=k+1;
wfront(k)=A(i,j);
z(1,k)=1;
z(2,k)=r*cos(theta);
z(3,k)=r*sin(theta);
z(4,k)=2*r^2-1;
z(5,k)=r^2*cos(2*theta);
z(6,k)=r^2*sin(2*theta);
z(7,k)=(3*r^3-2*r)*cos(theta);
z(8,k)=(3*r^3-2*r)*sin(theta);
z(9,k)=6*r^4-6*r^2+1;
z(10,k)=r^3*cos(3*theta);
z(11,k)=r^3*sin(3*theta);
z(12,k)=(4*r^4-3*r^2)*cos(2*theta);
z(13,k)=(4*r^4-3*r^2)*sin(2*theta);
z(14,k)=(10*r^5-12*r^3+3*r)*cos(theta);
z(15,k)=(10*r^5-12*r^3+3*r)*sin(theta);
z(16,k)=20*r^6-30*r^4+12*r^2-1;
end
end
end
orthop=zeros(zj,k);
orthop(1,1:k)=z(1,:);
bb(1)=wfront*orthop(1,:)'/(orthop(1,:)*orthop(1,:)');
zterm=zj;
for n=2:zterm
orthop(n,:)=z(n,:);
for m=1:n-1
aa(n,m)=z(n,:)*orthop(m,:)'/(orthop(m,:)*orthop(m,:)');
orthop(n,:)=orthop(n,:)-aa(n,m)*orthop(m,:);
end
bb(n)=wfront*orthop(n,:)'/(orthop(n,:)*orthop(n,:)');
end
coef(zterm)=bb(zterm);
for n=1:zterm-1
coef(zterm-n)=bb(zterm-n)-coef(zterm-n+1:zterm)*aa(zterm-n+1:zterm,zterm-n);
end
coef_qulijiao=coef;
coef_qulijiao(1:4)=0;
r=0;
zz=zeros([1 zterm]);
for i = 1:M0
for j = 1:N0
rad = sqrt((i-RX)^2+(j-RY)^2);
if rad <= R0
r = rad/R0;
if r~=0
theta = atan2(RX-i,j-RY);
end
zz(1)=1;
zz(2)=r*cos(theta);
zz(3)=r*sin(theta);
zz(4)=2*r^2-1;
zz(5)=r^2*cos(2*theta);
zz(6)=r^2*sin(2*theta);
zz(7)=(3*r^3-2*r)*cos(theta);
zz(8)=(3*r^3-2*r)*sin(theta);
zz(9)=6*r^4-6*r^2+1;
zz(10)=r^3*cos(3*theta);
zz(11)=r^3*sin(3*theta);
zz(12)=(4*r^4-3*r^2)*cos(2*theta);
zz(13)=(4*r^4-3*r^2)*sin(2*theta);
zz(14)=(10*r^5-12*r^3+3*r)*cos(theta);
zz(15)=(10*r^5-12*r^3+3*r)*sin(theta);
zz(16)=20*r^6-30*r^4+12*r^2-1;
% fitted(i,j) =coef*zz';
fitted_qulijiao(i,j)=coef_qulijiao*zz';
end
end
end
if coef(4)>0
Result_qulijiao=fitted_qulijiao./(4*pi);
else
Result_qulijiao=(-1)*fitted_qulijiao./(4*pi);
end
figure(9),mesh(double(Result_qulijiao));
3 仿真结果
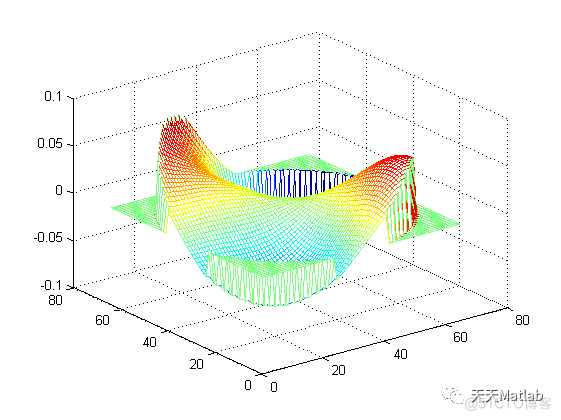
 编辑
编辑
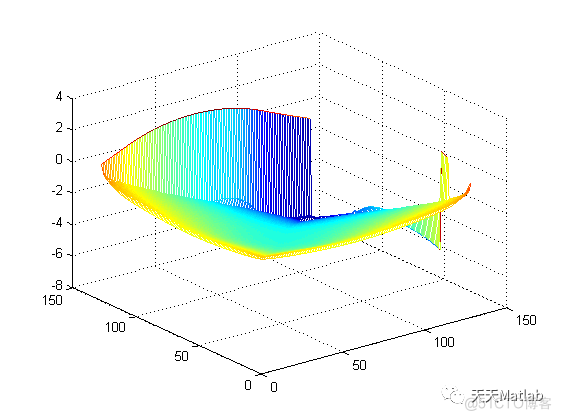
 编辑
编辑
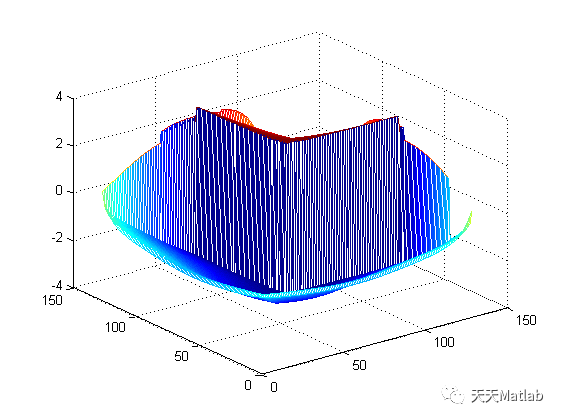
 编辑
编辑
4 参考文献
[1]钱晓凡, 饶帆, 李兴华,等. 精确最小二乘相位解包裹算法[J]. 中国激光, 2012, 39(2):5.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。

 编辑
编辑
