昨天听说今天是欢乐赛
然后就欢乐地被 IOI 血虐……
A. Lex String
B. Mystic Permutation
C. Infected Tree
D. Lena and Matrix
E. ANDfinity
然后就没有然后了
赛时得分: $500/500$ ,好像又AK了?疑惑
我这么菜不应该啊……
赛时排行:显然的 $Rank1$
赛前找化学戴老师找积累本,耽误了一些时间
然后电脑没开机没配置……等到Creator_157大佬AC了一道题才开题……
有点慌觉得自己凉凉
就先看T1,好像是道是字符串鬼题
A. Lex String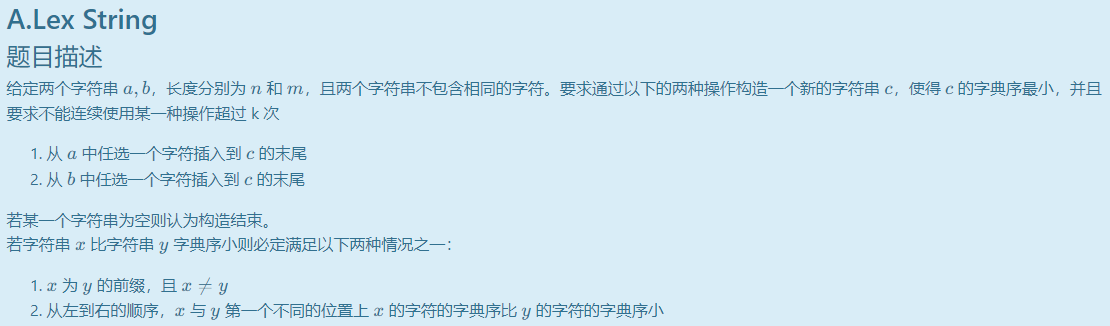
一开始看到想的是用 $char$ 维护
然鹅发现很恶心,想起 $string$ 里有一些有用的函数
于是改了 $string$,降序排列方便操作(其实用 $char$ 也不是不行
然后切了

#include<cstdio> #include<cstring> #include<string> #include<iostream> #include<algorithm> #define int long long #define WR WinterRain using namespace std; const int WR=10010000,mod=1e9+7; int t; int n,m,k; int read(){ int s=0,w=1; char ch=getchar(); while(ch>'9'||ch<'0'){ if(ch=='-') w=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ s=(s<<3)+(s<<1)+ch-48; ch=getchar(); } return s*w; } bool cmp(char x,char y){ return x>y; } signed main(){ t=read(); while(t--){ n=read(),m=read(),k=read(); string a,b,c; cin>>a;cin>>b; sort(a.begin(),a.end(),cmp); sort(b.begin(),b.end(),cmp); int lena=0,lenb=0; while(a.size()&&b.size()){ bool cmp=b.back()<a.back(); if(cmp&&lenb==k) cmp=false; if(!cmp&&lena==k) cmp=true; if(cmp) c.push_back(b.back()),b.pop_back(),lenb++,lena=0; else c.push_back(a.back()),a.pop_back(),lena++,lenb=0; } cout<<c<<endl; } return 0; }View Code
B. Mystic Permutation

纯暴力模拟即可
把元素从小到大插入,如果遇到了相同的或者用过的就跳过。
但是这样会出现一种情况那就是原序列的最后一个元素是 $n$ ,
那么放到最后一个元素的时候就只剩下了 $n$,那 么就无论如何也无法放置了。
这个问题也非常好解决:最后的这个元素 $n$ 我们肯定不能放在很靠前的位置,因为这样很明显字典序不会最小,
那么为了使得这个元素放得下我们就放在 $n−1$ 的位置上,
让 $n−1$ 的位置上原本应该放的元素放到 $n$ 上,
这样能保证前 $n−2$ 个一定是最小的,而不存在一种别的方法使得可以使得最后的两个元素比我们现在放置的更小,而且前 $n−2$ 个依旧保持最小。

#include<cstdio> #include<cstring> #include<string> #include<iostream> #include<algorithm> #define int long long #define WR WinterRain using namespace std; const int WR=1001000,mod=1e9+7; int t; int n,a[WR]; bool flag[WR]; int read(){ int s=0,w=1; char ch=getchar(); while(ch>'9'||ch<'0'){ if(ch=='-') w=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ s=(s<<3)+(s<<1)+ch-48; ch=getchar(); } return s*w; } signed main(){ t=read(); while(t--){ n=read(); for(int i=1;i<=n;i++) a[i]=read(),flag[i]=false; if(n==1){ printf("-1\n"); continue; } for(int i=1;i<=n-2;i++){ int tmp=1; while(flag[tmp]||tmp==a[i]) tmp++; printf("%lld ",tmp); flag[tmp]=true; } int x=0,y=0; for(int i=1;i<=n;i++){ if(!flag[i]){ if(!x) x=i; else y=i; } } if(x!=a[n-1]&&y!=a[n]) printf("%lld %lld\n",x,y); else printf("%lld %lld\n",y,x); } return 0; }View Code
C. Infected Tree

这是个动态规划啊……
还是一个比较基础的树形DP
考虑为尽可能多的保留节点,我们每一次肯定是会删除被病毒感染的节点的某个子节点,
而删除之后我们的问题就可以转化为它的另一个儿子(注意为二叉树)根被感染病毒能保留多少节点的子问题,
那么这很明显就可以考虑一下 DP。
DP 状态也很简单: dp[i] 表示以 i 为根的子树若 i 被感染病毒,最多能保留多少节点
那么下面就是考虑转移了,转移很明显就是我们考虑删除哪一个 i 的子节点就好了,因为是二叉树所以不用考 虑更多的情况。
那么我们就分别考虑究竟删除哪一个子节点。
假设删除 son1,那么相当于在 son1 的子树里我们可以保留下 size[son1]−1 个节点,size[i] 代表以 i 为根的子 树的大小(包含节点 i),
而在 son2 的子树里,我们依旧可以保留下 dp[son2] 个节点,所以最终的状态就 是:
$dp[i]=max(dp[son1]+size[son2]−1,dp[son2]+size[son1]−1)$
需要注意可能该子树为空,那么 size[son]−1 就是一个负数,所以需要对 0 取 max,
为避免这种情况 先进行 dfs 再更新 sz 和 dp,以及多组数据所以每次需要将各种数组清零,清零 head 数组也相当于清零边的数组

#include<cstdio> #include<cstring> #include<string> #include<iostream> #include<algorithm> #define int long long #define WR WinterRain using namespace std; const int WR=1001000,mod=1e9+7; struct Edge{ int pre,to; }edge[WR]; int t; int n,sze[WR]; int head[WR],tot; int dp[WR]; int read(){ int s=0,w=1; char ch=getchar(); while(ch>'9'||ch<'0'){ if(ch=='-') w=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ s=(s<<3)+(s<<1)+ch-48; ch=getchar(); } return s*w; } void add(int u,int v){ edge[++tot].pre=head[u]; edge[tot].to=v; head[u]=tot; } void dfs(int u,int root){ sze[u]=1,dp[u]=0;//dp数组存储如果我被感染了能活多少个 int sum=0; for(int i=head[u];i;i=edge[i].pre){ int v=edge[i].to; if(v!=root){ dfs(v,u); sum+=dp[v]; sze[u]+=sze[v]; } } for(int i=head[u];i;i=edge[i].pre){ int v=edge[i].to; if(v!=root){ dp[u]=max(dp[u],sum-dp[v]+sze[v]-1); } } } signed main(){ t=read(); while(t--){ n=read(); tot=0; for(int i=1;i<=n;i++) head[i]=0; for(int i=1;i<n;i++){ int u=read(),v=read(); add(u,v); add(v,u); } dfs(1,0); printf("%lld\n",dp[1]); } return 0; }View Code
D. Lena and Matrix

要求的是最大值最小,其实发现这个最大值不是和任意一个黑色格子的距离都有可能成为最大值的,
能成为最大距离的黑色格子一定是最左上、右下、左下、右上的黑格子,
可以发现如果不是这四个格子,那么把距离转化到这四个黑色格子上都一定可以增加
下面就是如何寻找着四个黑色格子的问题了。
考虑如果一个格子离左上角越近,x 越小,y 越小,而且 x 与 y 的减小,对其离左上角的距离产生的贡献是一样 的,
那么就直接令这个贡献为 x+y,那么最左上角的点也就一定是贡献最小的点,最右下角的点也一定是贡献 最大的点,这就解决了两个。
考虑如果一个格子离右上角越近,x 越大,y 越小,而且它们产生的贡献也都是一样的,所以就考虑直接令贡献 为 x−y,
这样最右上的点也就是 x−y 最大点,最左下的点也就是 x−y 最小的点,至此四个点全部解决了。
那么就是要找一个位置使得这个位置到这四个位置的距离最大值最小,就直接枚举每一个位置寻找一下就 好了

#include<cstdio> #include<cstring> #include<string> #include<iostream> #include<algorithm> #define int long long #define WR WinterRain using namespace std; const int WR=1001,mod=1e9+7; int t; int n,m; int mp[WR][WR]; pair<int,int>w,a,s,d; int read(){ int s=0,w=1; char ch=getchar(); while(ch>'9'||ch<'0'){ if(ch=='-') w=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ s=(s<<3)+(s<<1)+ch-48; ch=getchar(); } return s*w; } signed main(){ t=read(); while(t--){ n=read(),m=read(); for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ char ch; cin>>ch; if(ch=='B') mp[i][j]=1; else mp[i][j]=0; } } w=a=s=d={0,0}; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ if(mp[i][j]){ if((w.first==0&&w.second==0)||i+j>w.first+w.second) w={i,j}; if((s.first==0&&s.second==0)||i+j<s.first+s.second) s={i,j}; if((a.first==0&&a.second==0)||i-j<a.first-a.second) a={i,j}; if((d.first==0&&d.second==0)||i-j>d.first-d.second) d={i,j}; } } } int ans=mod; pair<int,int>res; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ int dis=-mod; dis=max(max(abs(i-w.first)+abs(j-w.second), abs(i-s.first)+abs(j-s.second)), max(abs(i-a.first)+abs(j-a.second), abs(i-d.first)+abs(j-d.second))); if(dis<ans){ ans=dis; res={i,j}; } } } printf("%lld %lld\n",res.first,res.second); } return 0; }View Code
E. ANDfinity

首先我们分析样例
对于第一组样例, 1 2 3 4 5
我们可以发现它其实本身就是联通的,因此不需要操作
然后看第五组样例, 3 0 0 0
输出是 3 1 1 1 ,说明它把所有的 0 都加了一
那么我们自然可以想到先把所有 0 加一再去判断是否连通
接着看到第二组样例, 0 2
将 0 变成 1 后只需要将 2 减去一或者将 1 加上一就可以保证连通
第三组样例同理,把 12 减去一即可
一般地,我们可以想到,对于一组起初不连通的数据,可以找出拥有最大的 $\operatorname{lowbit}$ 的数字,将这个数字减一
它减一后所有的低于它的 $\operatorname{lowbit}$ 的数位都会变成 1
这样,因为它的 $\operatorname{lowbit}$ 是最大的,它减一后的数字必然有一位与其它数字中的某一位做与运算后不为 0
举个例子,对于 8 4 2 3 ,显然的, 8 的 $\operatorname{lowbit}$ 值是最大的
我们让 8 减去一 ,然后 $ ( 1000 )_2 $ 变成了 $ (111)_2 $
它与 $ 4 = (100)_2$ ,$ 2 = (10)_2 $ ,$ 3 = (11)_2 $ 都有共同的一位为 1
整张图便连通了
这样我们就分析完了样例,AC 似乎就在眼前……吗?
然鹅就这样写是会挂的
不妨考虑如下的一组数据 8 8 1
如果将第一个 8 减一,数据变为 $(111)_2$ ,$(1000)_2$ ,$(1)_2$
这样图是不连通的,如果再将第二个 8 减一就错了
因为我们很容易发现将某个 8 加一就可以变成 $(1001)_2$ ,$(1000)_2$ ,$(1)_2$ ,这样图是连通的
所以我们可以得出结论,可以尝试把某个点加一或者减一,然后判断连通性
但是这样还是不完美,考虑下一组数据 2 4 12 ,也就是 $(10)_2$ ,$(100)_2$ ,$(1100)_2$
4 和 12 的 $\operatorname{lowbit}$ 值都是 4
显然的让某个数加一或者让某个数减一都无法保证连通( 可以自己试一试 )
所以我们让一个数加一,另一个数减一,数据变为 $(10)_2$ ,$(11)_2$ ,$(1101)_2$
这样终于可以保证连通了
然后注意操作数要加上一开始初始化 0 为 1 的操作数
关于如何判断连通性,可以考虑维护一些边,每次找到两个相邻的为 1 的位连边
比如 $(101100)_2$ ,我们考虑给第一位和第三位,第三位和第四位连双向边
这样只要遍历出边就可以找到所有 这一位是一的数 的所有为 1 的位,再去扫这几位的出边
这样可以一直递归下去打下标记,最后再判断是否连通即可
说起来很艰难,具体见代码

#include<cstdio> #include<cstring> #include<string> #include<iostream> #include<algorithm> #define int long long #define WR WinterRain using namespace std; const int WR=5010,mod=1e9+7; int t; int n,ans,a[WR]; int bit[WR/50][WR]; bool flag[WR/50]; int read(){ int s=0,w=1; char ch=getchar(); while(ch>'9'||ch<'0'){ if(ch=='-') w=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ s=(s<<3)+(s<<1)+ch-48; ch=getchar(); } return s*w; } void tag(int u){ if(flag[u]) return; flag[u]=true; for(int i=1;i<=bit[u][0];i++){ tag(bit[u][i]); } } bool judge(){ int s=0; memset(flag,false,sizeof(flag)); memset(bit,0,sizeof(bit)); for(int i=1;i<=n;i++){ if(!a[i]) return false; s|=a[i]; } for(int i=1;i<=n;i++){ int pre=-1; for(int j=0;j<=30;j++){ if(a[i]&(1<<j)){ if(pre!=-1){ bit[pre][0]++,bit[j][0]++; bit[pre][bit[pre][0]]=j,bit[j][bit[j][0]]=pre; } pre=j; } } } for(int i=0;i<=30;i++){ if(s&(1<<i)){ tag(i); break; } } for(int i=0;i<=30;i++){ if((s&(1<<i))&&!flag[i]) return false; } return true; } int lowbit(int x){ return x&(-x); } signed main(){ t=read(); while(t--){ n=read(); bool tag=false; for(int i=1;i<=n;i++) a[i]=read(); ans=0; for(int i=1;i<=n;i++){ if(!a[i]) ans++,a[i]++; } if(judge()){ printf("%lld\n",ans); for(int i=1;i<=n;i++){ printf("%lld ",a[i]); } printf("\n"); continue; } for(int i=1;i<=n;i++){ a[i]--; if(judge()){ printf("%lld\n",ans+1); for(int j=1;j<=n;j++){ printf("%lld ",a[j]); } printf("\n"); tag=true; break; } a[i]++; } if(tag) continue; for(int i=1;i<=n;i++){ a[i]++; if(judge()){ printf("%lld\n",ans+1); for(int j=1;j<=n;j++){ printf("%lld ",a[j]); } printf("\n"); tag=true; break; } a[i]--; } if(tag) continue; int low=0; for(int i=1;i<=n;i++) low=max(low,lowbit(a[i])); for(int i=1;i<=n;i++){ if(lowbit(a[i])==low){ a[i]--; break; } } for(int i=1;i<=n;i++){ if(lowbit(a[i])==low){ a[i]++; break; } } printf("%lld\n",ans+2); for(int i=1;i<=n;i++){ printf("%lld ",a[i]); } printf("\n"); } return 0; }View Code

