线性回归的梯度下降法之原理总结与代码实战

文章目录

• ​​1. 一元线性回归​​

• ​​1.1 梯度下降​​
• ​​1.2 随机梯度下降​​

• ​​2. 多元线性回归​​

1. 一元线性回归

  对于一元线性回归而言，本质上是找到最优线性模型对应的参数a(斜率)、b(截距)。最原始的方法是通过​​穷举​​法计算每组参数的损失函数，然后通过损失函数取值最小得到最优参数。

  Q：穷举法求解的缺点是什么？

  一元线性回归的损失函数是

L ( a , b ) = 1 n ∑ i = 1 n ( a x i + b − y i ) 2 L(a, b)=\frac{1}{n}\sum_{i=1}^{n}(ax_{i}+b-y_{i})^2 L(a,b)=n1​i=1∑n​(axi​+b−yi​)2

  Q：线性模型的损失函数和统计学习方法中最先定义的损失函数有什么差别呢？

  A：线性函数的损失函数是MSE，而统计学习方法定义的损失函数是平方损失，并不会求均值。

  Q：求均值的好处是什么呢？

  A：不求均值的话，求导值可能过大，容易造成梯度爆炸。

  偏导数分别为：

∂ L ∂ a = ∑ i = 1 n 2 n x i ( a x i + b − y i ) \frac{\partial L}{\partial a}=\sum_{i=1}^{n}\frac{2}{n}x_{i}(ax_{i}+b-y_{i}) ∂a∂L​=i=1∑n​n2​xi​(axi​+b−yi​)

∂ L ∂ b = ∑ i = 1 n 2 n ( a x i + b − y i ) \frac{\partial L}{\partial b}=\sum_{i=1}^{n}\frac{2}{n}(ax_{i}+b-y_{i}) ∂b∂L​=i=1∑n​n2​(axi​+b−yi​)

  以一组简单的数据为例，具体代码和图像表示如下：

import numpy as np
import matplotlib.pyplot as plt

x = np.array([1., 2., 3., 4., 5.])
y = np.array([1., 3., 2., 3., 5.])
plt.scatter(x , y)
plt.show()

1.1 梯度下降

  从算法的思想上来看，每一次迭代都是朝下降最快的方向移动，本质上属于​​贪心​​算法。贪心算法不一定能得到全局最优解（除非是在凸函数），但是至少能得到局部最优解（非凸函数）。

  代码表示如下：

a = b = 0 #假设斜率和偏置项均为0
eta = 0.001
epsilon = 1e-8
times = 0

while True:
partial_a = 2 * sum(x * (a*x + b -y))
partial_b = 2 * sum((a * x + b -y))

if abs(partial_a) < epsilon and abs(partial_b) < epsilon:
break

a, b = a - eta * partial_a, b - eta * partial_b
times += 1
print('a is {}, b is {}, times is {}'.format(a, b, times))

  结果为a is 0.8000000016366973, b is 0.399999994091004, times is 10136。

1.2 随机梯度下降

  Q：随机梯度下降相比于梯度下降有什么好处呢？

  A：随机梯度下降相比于梯度下降有可能能越过​​鞍点​​。

  Q：随机梯度下降有什么缺点呢？

  A：如果能够提前进行预计算梯度，分别对梯度下降和随机梯度下降进行计算的话，前者本质上只需计算并存储所有样本的梯度之和。而后者需要保存所有单个样本的梯度，那么就会占用大量的空间。为了折中，则产生了小批量梯度下降法。

def loss(x, y, a, b):
return sum((a * x + b - y) ** 2)

eta = 0.01
a = b = 0
epsilon = 1e-5 #如果设为1e-8，很久也跑不出结果
times = 0

while True:
rand = np.random.randint(low=0, high = x.size)
partial_a = 2* x[rand] * (a*x[rand] + b - y[rand])
partial_b = 2 *(a * x[rand] + b -y[rand])

last_loss = loss(x, y, a, b)
print('loss is', last_loss)
a, b = a - eta * partial_a, b - eta * partial_b
cur_loss = loss(x, y, a, b)

if (abs(cur_loss - last_loss) < epsilon):
break

times += 1

结果如下所示：

  使用keras，代码如下所示：

import tensorflow as tf
import numpy as np
from tensorflow import keras
model = tf.keras.Sequential([keras.layers.Dense(units=1, input_shape=[1])])
model.compile(optimizer='sgd', loss='mean_squared_error')
xs = np.array([1.0, 2.0, 3.0, 4.0, 5.0], dtype=float)
ys = np.array([1.0, 3.0, 2.0, 3.0, 5.0], dtype=float)
model.fit(xs, ys, epochs=1000)
print(model.predict([7.0]))

  结果如下所示：

Epoch 1/1000
5/5 [==============================] - 1s 105ms/sample - loss: 44.1191
Epoch 2/1000
5/5 [==============================] - 0s 1ms/sample - loss: 25.9117
Epoch 3/1000
5/5 [==============================] - 0s 429us/sample - loss: 15.3013
Epoch 4/1000
5/5 [==============================] - 0s 883us/sample - loss: 9.1180
Epoch 5/1000
5/5 [==============================] - 0s 837us/sample - loss: 5.5147
Epoch 6/1000
5/5 [==============================] - 0s 815us/sample - loss: 3.4149
Epoch 7/1000
5/5 [==============================] - 0s 707us/sample - loss: 2.1912
Epoch 8/1000
5/5 [==============================] - 0s 794us/sample - loss: 1.4781
Epoch 9/1000
5/5 [==============================] - 0s 724us/sample - loss: 1.0626
Epoch 10/1000
5/5 [==============================] - 0s 844us/sample - loss: 0.8204
Epoch 11/1000
5/5 [==============================] - 0s 396us/sample - loss: 0.6793
Epoch 12/1000
5/5 [==============================] - 0s 281us/sample - loss: 0.5970
Epoch 13/1000
5/5 [==============================] - 0s 286us/sample - loss: 0.5491
Epoch 14/1000
5/5 [==============================] - 0s 315us/sample - loss: 0.5211
Epoch 15/1000
5/5 [==============================] - 0s 315us/sample - loss: 0.5048
Epoch 16/1000
5/5 [==============================] - 0s 303us/sample - loss: 0.4953
Epoch 17/1000
5/5 [==============================] - 0s 388us/sample - loss: 0.4898
Epoch 18/1000
5/5 [==============================] - 0s 336us/sample - loss: 0.4866
Epoch 19/1000
5/5 [==============================] - 0s 351us/sample - loss: 0.4847
Epoch 20/1000
5/5 [==============================] - 0s 283us/sample - loss: 0.4836
Epoch 21/1000
5/5 [==============================] - 0s 327us/sample - loss: 0.4829
Epoch 22/1000
5/5 [==============================] - 0s 333us/sample - loss: 0.4825
Epoch 23/1000
5/5 [==============================] - 0s 318us/sample - loss: 0.4823
Epoch 24/1000
5/5 [==============================] - 0s 307us/sample - loss: 0.4822
Epoch 25/1000
5/5 [==============================] - 0s 277us/sample - loss: 0.4821
Epoch 26/1000
5/5 [==============================] - 0s 365us/sample - loss: 0.4820
Epoch 27/1000
5/5 [==============================] - 0s 361us/sample - loss: 0.4820
Epoch 28/1000
5/5 [==============================] - 0s 296us/sample - loss: 0.4819
Epoch 29/1000
5/5 [==============================] - 0s 328us/sample - loss: 0.4819
Epoch 30/1000
5/5 [==============================] - 0s 387us/sample - loss: 0.4819
Epoch 31/1000
5/5 [==============================] - 0s 367us/sample - loss: 0.4819
Epoch 32/1000
5/5 [==============================] - 0s 288us/sample - loss: 0.4819
Epoch 33/1000
5/5 [==============================] - 0s 298us/sample - loss: 0.4819
Epoch 34/1000
5/5 [==============================] - 0s 299us/sample - loss: 0.4818
Epoch 35/1000
5/5 [==============================] - 0s 370us/sample - loss: 0.4818

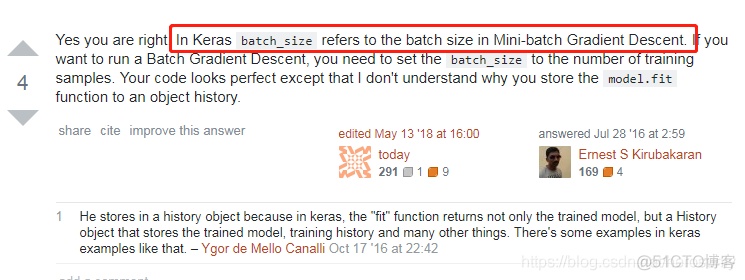
  loss基本上不变，原因在于Keras中的SGD指的并不是随机梯度下降，而是小批量随机梯度下降（https://stats.stackexchange.com/questions/221886/how-to-set-mini-batch-size-in-sgd-in-keras）。

2. 多元线性回归

  多元相比于一元而言，自变量就从单个变成了多个。如果依然使用​​穷举​​法，那么计算和比较的成本就会指数级增长。

  Q：能否使用​​分治​​法减少计算量呢？

  A：不可以。除非损失函数是光滑的凸函数。